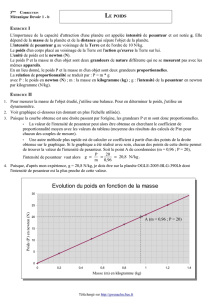
Le champ de pesanteur

A
AB
F
B
BA
F
d
P
g
Verticale de A
A
z
P
Le champ de pesanteur
Document 1 : Poids d’un corps
Le poids d’un corps A de masse m est la force exercée par la Terre sur le
corps situé dans son voisinage.
La Terre modifie les propriétés de l’espace dans son voisinage : elle crée un
champ vectoriel appelé champ de pesanteur qu’on note
g
.
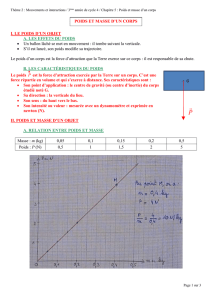
Relation entre le poids et le champ de pesanteur : P = m . g
Unités : g en N.kg-1, P en Newton (N) et m en kilogramme (kg)
Remarque :
La masse d’un objet représente sa quantité de matière ; elle a toujours la même valeur quelque soit le
lieu où on la mesure.
Le poids d’un objet est une force qui caractérise la « lourdeur » du corps ; il dépend de la pesanteur du
lieu où se trouve l’objet.
Document 2 : La force gravitationnelle
L’interaction gravitationnelle entre deux corps est due aux masses des deux corps.
C’est Isaac Newton (1643-1727) qui propose une modélisation de l’interaction gravitationnelle : deux
corps A et B, séparés par une distance d = AB et de masses respectives mA et mB, sont soumis à deux
forces directement opposées, dont l’intensité est proportionnelle au produit des masses et
inversement proportionnelle au carré de la distance qui sépare ces masses :
2
dmm
GFF BA
ABBA
Unités :
FAB et FBA en Newton (N)
mA et mB en kilogramme (kg)
d est en mètre (m)
et G=6,67×10-11N.m2.kg-2 G est appelée constante gravitationnelle
Les questions suivantes visent à établir une expression du champ de pesanteur
1. Compléter le schéma qui traduit l’interaction gravitationnelle
existant entre la Terre de masse MT et un objet (bonhomme) de
masse m à la surface de la Terre.
2. Donner l’expression de l’intensité de la force
BT
F
exercée par la
Terre sur le bonhomme, en fonction de m, MT, RT et G.
3. En assimilant la force
BT
F
au poids
P
de l’objet, exprimer g
l’intensité de la pesanteur en fonction de G, MT, RT.
4. Exprimer l’intensité g du champ de pesanteur à la surface de la
Terre pour l’altitude z=0. Calculer sa valeur sachant que
MT=5,98.1024kg et RT=6,38.106m.
5. Par analogie à l’expression du champ de pesanteur établie précédemment,
donner l’expression du champ de pesanteur
zg
à l’altitude z au-dessus de la
surface de la Terre.
Calculer la valeur de l’intensité de la pesanteur à l’altitude z = 10 km.
RT

6. Exprimer l’intensité de la pesanteur gL créée par la Lune à sa surface en fonction de G, ML et RL
(masses et rayons de la Lune).
Calculer gL sachant que la masse de la Lune (ML = 7,5×1022 kg ; RL = 1,74×106 m). La comparer à
l’intensité de la pesanteur à la surface de la terre.
La gravitation universelle : une balance pour l’univers
On cherche à utiliser la loi de gravitation établie par Newton pour déterminer la masse du Soleil.
Document 3 : Loi de Képler
Quelques déceniies avant Newton, Johannes Kepler, né le 27 décembre 1571 à Weil
der Stadt, près de Stuttgart (Allemagne), mort le 15 novembre 1630 à Ratisbonne, a
étudié et confirmé l'hypothèse héliocentrique (la Terre tourne autour du Soleil) de
Nicolas Copernic. Il a également découvert que les trajectoires des planètes n’étaient
pas des cercles parfaits centrés sur le Soleil mais des ellipses. En outre, il a énoncé à
partir d’oservations les lois (dites lois de Kepler) qui régissent les mouvements des
planètes sur leurs orbites, dont est donné un énoncé de la 3ème ci-dessous :
3ème loi de Képler : Le carré de la période des objets en orbite est proportionnel au cube du rayon de
leur trajectoire.
Remarque : la période T d’un objet en orbite est la durée d’1 tour autour de l’astre attracteur.
Document 4 : la confirmation de Newton
Quelques dizaine d’années après les observations de Képler, Newton établit en utilisant la loi de
gravitation que la relation entre T2 et R3 s’exprimait de façon suivante :
3
2
24R
GM
T
Où M est la masse de l’astre autour duquel gravitent les satellites.
Document 5 : Les planètes du système solaire sont les satellites du Soleil
Nom
Rayon de l’orbite
(× 109 m)
Période T
(jours)
Mercure
58
88
Vénus
109
225
Terre
150
365
Mars
228
686
Jupiter
781
4330
Saturne
1431
10751
Uranus
2879
30666
Neptune
4510
60145
Pluton
5922
90666
7. A partir des documents 3, 4 et 5, proposer une méthode qui permet de déterminer la masse de
Jupiter.
8. Chercher la valeur de la masse du Soleil donnée par une encyclopédie. Comparer avec la valeur issue
de votre étude.

Aide partie 2 :
 Quelle courbe veut-on obtenir pour vérifier la proportionnalité ? Quelle graphique doit –on alors
tracer (quoi en fonction de quoi ?)
 Quelle sont les grandeurs à calculer ?
 Compléter le tableau et tracer le graphique prévu :
 Commenter le graphique obtenu (peut-on confirmer que la loi de Képler est vérifiée ?) :
 Modéliser la courbe obtenue
 Calculer la masse de Jupiter en utilisant le coefficient directeur issu du modèle.