Exercice Tintin correction

!""#$%&'()#*)#+$),')#*)-(*.$/*0+1)&1$.'(2'##')'1)2&""+2*1/)%&')#')3+("2)!)('"(42'1/')5$101)
'/)%&')6)('"(42'1/')#*)5'((')7))
89 ):;"($<'()#*)=+(3')-(*.$/*0+11'##')';'(34')"*()#*)5'((')2&()5$101)#+(2%&>$#)'2/)2$/&4)?)
#*)2&(=*3'),')#*)5'((')@))
)89)A+$/)<0101)#*)<*22'),')5$101))))
)
T/tint in
F=G!tint in
m!Mterre
RTerre
2
B9 ):1),4,&$(')#>';"('22$+1)#$C4(*#'),')#*)"'2*1/'&()/'(('2/(')1+/4')-5)D2&()5'(('9E)
F&'##')'2/)2*).*#'&()@))
)B9)G+<<')H5I0101)J)K)J)<0101);)-5))*#+(2)
)
T
g=G!Mterre
RTerre
2
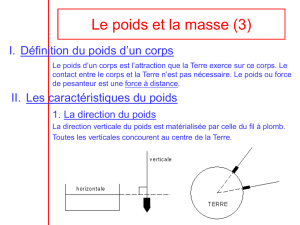
L9)F&'##')'2/),+13)#>+($-$1'),')#*)"'2*1/'&()/'(('2/(')@) ))
L9)M>+($-$1'),')#*)"'2*1/'&()/'(('2/(')'2/)#$4')?)#*)=+(3')-(*.$/*0+11'##')%&$)';$2/')'1/(')B)
+NO'/2E)
)
P9)Q4R1$()#')"+$,2)2&()#*)#&1')"&$2)"(+34,'(),')#*)<S<')=*T+1)"+&()/(+&.'()#>';"('22$+1)
"&$2)#*).*#'&(),')#*)"'2*1/'&()#&1*$(')-M)D2&()#*)#&1'9E) ))
P9)KM)J)<);)-M))*.'3))
)
L
g=G!Mlune
lune
2
R

U9)5$101),$/V$#).(*$)#+(2),')2+1)';"#$3*0+1)*&)3*"$/*$1')W*,,+3X)@)K+&(%&+$)#')N+1,),&)
3*"$/*$1')'2/)$#)';3'"0+11'#)@))
U9)G*#3&#+12)#')(*""+(/),'2)"'2*1/'&(2)7))-5)I)-M)J)YZ[)I)8Z\)J)\Z8E)]&$Z)5$101),$/).(*$)#*)
"'2*1/'&()2&()#*)#&1')'2/)\)=+$2)"#&2)=*$N#')'/),+13)+1)"'&/)^)=*$('),'2)N+1,2)';3'"0+11'#2)
\9):1)2&""+2*1/)%&')#*)<*22'),&)3*"$/*$1')W*,,+3X)2+$/),')[P)X-)'/)%&')3'##'),')2+1)
4%&$"'<'1/)2+$/),')88_)X-)3*#3&#'()#')"+$,2),&)3*"$/*$1')W*,,+3X)
)\9)K3*"$/*$1')J)</+/*#');)-M)J)D88_`[P9);)8Z\)J)L8_ZP)a)
b9)A&()%&'#)*2/('),&)2^2/c<')2+#*$(')#')3*"$/*$1')W*,,+3X)"+&((*$/)=*$(')&1)N+1,)'13+(')
"#&2)$<"('22$+11*1/)@)A&()%&'#)*2/(')#')N+1,),&)3*"$/*$1')W*,,+3X)2>*""*('1/'(*$/)?)&1)
2*&/),')"&3')@))

b9)A&()%&'#)*2/('),&)2^2/c<')2+#*$(')#')3*"$/*$1')W*,,+3X)"+&((*$/)=*$(')&1)N+1,)'13+(')
"#&2)$<"('22$+11*1/)@)A&()%&'#)*2/(')#')N+1,),&)3*"$/*$1')W*,,+3X)2>*""*('1/'(*$/)?)&1)
2*&/),')"&3')@))
b9)]1)"'&/)(4*#$2'()#')3*#3&#),'),$d4('1/'2)"'2*1/'&(2)'1)&0#$2*1/)#'2),+114'2),')
,$d4('1/'2)"#*1c/'2)'/)4/+$#'27)
V e1/'12$/4),')"'2*1/'&(),')Gf*(+1)D2*/'##$/'),')K#&/+19Z))-3f*(+1)J)_ZB[)aE)X-V8)
V e1/'12$/4),')"'2*1/'&(),')#*)M&1')D2*/'##$/'),')#*)5'(('9Z))-M)J)8Z\)aE)X-V8)
V e1/'12$/4),')"'2*1/'&(),')g*(2Z))-g*(2)J)LZb)aE)X-V8)
V e1/'12$/4),')"'2*1/'&(),')#*)5'(('Z))-5)J)YZ[)aE)X-V8)
V e1/'12$/4),')"'2*1/'&(),')h&"$/'(Z))-h&"$/'()J)BUZY)aE)X-V8)
V e1/'12$/4),')"'2*1/'&(),&)A+#'$#Z))-A)J)BbP)aE)X-V8)
V e1/'12$/4),')"'2*1/'&(),>&1)5(+&)a+$(),')L)X<Z))-/(+&i1+$())J)\E8_B8)aE)X-V8)
)
planète
g=G!planète
M
Rplanète
2