Sans titre

Chapitre 3
Rotation autour d’un axe fixe
Dans le chapitre pr´ec´edent, nous avons vu qu’un solide peut tourner sur lui-mˆeme sous l’action du moment
d’une force. Nous allons donc nous int´eresser `a la rotation d’un solide sur lui-mˆeme en comman¸cant par le cas
le plus simple possible, `a savoir, la rotation autour d’un axe fixe.
Si l’axe de rotation passe par G, le centre de masse du solide, alors ce point est immobile et ~p=~ 0. L’impulsion
ne permet donc pas de d´ecrire ce mouvement et il nous faut trouver un autre outil math´ematique pour ´etudier
la rotation. Par ailleurs, tous les points du solide n’ont pas la mˆeme vitesse. Comment d´ecrire la rotation ?
3.1 Vecteur rotation
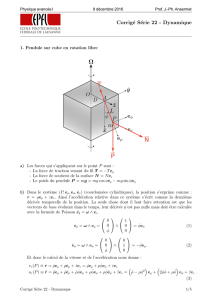
Consid´erons donc un solide en rotation autour d’un axe fixe , comme sur la figure 3.1. Chaque point du
solide a un mouvement de rotation autour de sa projection sur l’axe, D. La vitesse de rotation, !,estlamˆeme
pour tous ces points. On va donc l’utiliser.
Afin de prendre en compte la direction de l’axe et le sens de rotation, on introduit le vecteur rotation ~! qui
est
— port´e par l’axe de rotation,
— orient´e en fonction du sens positif de rotation choisi, en suivant la r`egle du tire-bouchon comme pour le
moment des forces,
— et de norme
k~! k=
d✓
dt 
.(3.1)
Ici, ✓est l’angle de rotation du solide.
Soient Oune origine choisie sur l’axe de rotation et Mun point quelconque du solide. Voir la figure 3.1. La
vitesse du point Mvaut
~v(M)=d!
OM
dt =d!
DM
dt =DM d~ur dt =DM d✓ dt ~u✓=DM d✓ dt ~uz^~ur=~! ^!
DM =~! ^! OM. (3.2)
Ainsi, pour un solide en rotation autour d’un axe fixe et Oun point de cet axe, la vitesse d’un
point Mquelconque de ce solide, est
~v(M)=~! ^! OM. (3.3)
Le mouvement de rotation du solide est bien caract´eris´e par la vitesse angulaire ~! qui permet de d´eduire
ais´ement la vitesse de chaque point du solide. C’est elle que l’on cherchera `a d´eterminer par la suite.
23

CHAPITRE 3. ROTATION AUTOUR D’UN AXE FIXE 24
Δ
O
DM
S
Figure 3.1 – Solide en rotation autour d’un axe 
3.2 Th´eor`eme du moment cin´etique
3.2.1 D´efinition du moment cin´etique
Pour un mouvement de translation, la r´esultante des forces est li´ee `a la quantit´e de mouvement via la relation
fondamentale de la dynamique. Pour un mouvement de rotation, nous avons vu dans le chapitre pr´ec´edent, que
c’est le moment d’une force qui en est `a l’origine. Pour connaˆıtre la r´eaction du solide `a l’action de ce moment
de force, il nous faut d´efinir une grandeur intitul´ee moment cin´etique qui est le moment de la quantit´e de
mouvement.
En m´ecanique du point, le moment cin´etique d’un point Mde masse mpar rapport `a un point Oest donc
d´efini par
~ o=! OM ^~p(M)=m! OM ^~v(M).(3.4)
Il a d´ej`a ´et´e vu pour l’´etude des mouvements des corps c´elestes o`u il correspond `a l’aire balay´ee, `a une constante
multiplicative pr`es.
On peut g´en´eraliser ais´ement cette d´efinition `a un solide en le divisant en ´el´ements dm puis en sommant sur
tout le solide :
~ o=ZZZS
!
OM ^~v(M)dm. (3.5)
Cette expression est complexe et difficilement utilisable ainsi. On va chercher `a la simplifier.
Alors que la quantit´e de mouvement est li´ee `a l’invariance par translation par le th´eor`eme de N¨other, le
moment cin´etique est li´e `a l’invariance par rotation. Depuis le d´ebut de vingti`eme si`ecle, nous savons donc
pourquoi la quantit´e de mouvement et le moment cin´etique sont les grandeurs pertinentes pour ´etudier les
mouvements de translation et de rotation respectivement. Pour rappel, l’´energie est li´ee `a l’invariance par
translation dans le temps.
3.2.2 Th´eor`eme du moment cin´etique pour un point mat´eriel
Pour connaˆıtre l’´evolution de l’orientation d’un solide, il nous faut consid´erer le moment cin´etique par rapport
`a un point Ofixe dans le r´ef´erentiel d’´etude, suppos´e galil´een. Comme pour l’impulsion, c’est sa d´eriv´ee par
rapport au temps qui va nous int´eresser. En m´ecanique du point, cela avait conduit au th´eor`eme du moment
cin´etique, rappel´e ici. Pour un point Mde masse m,
d~o
dt =md!
OM
dt ^~v+m!
OM ^d~v
dt =m!
OM ^~a
=! OM ^~ Fext =~ M~
Fext /O.(3.6)

CHAPITRE 3. ROTATION AUTOUR D’UN AXE FIXE 25
Pour un point mat´eriel, toutes les forces sont appliqu´ees en M.
La structure de cette ´equation est similaire `a celle de la relation fondamentale de la dynamique.
3.2.3 Th´eor`eme du moment cin´etique pour un solide
En m´ecanique du solide on aura la mˆeme relation en sommant tous les moments des forces ext´erieures par
rapport `a Ocalcul´es au point d’application de chacune des forces,
d~o
dt =X~
M~
Fext /O =X!
OAi^~ Fi,(3.7)
les forces int´erieures se compensant. Dans cette expression, Aiest le point d’application de la force ~ Fi. En cas
de forces continues comme le poids, la somme devient une int´egrale triple sur tout le volume. L`a encore, le point
Oest suppos´e fixe dans un r´ef´erentiel galil´een.
Cette loi est g´en´erale et nous sera utile tout au long du cours car elle permet d’´etudier la rotation due au
moment des forces. Elle vient compl´eter le th´eor`eme de la r´esultante cin´etique qui permet d’´etudier le mouvement
du centre de masse de l’objet. Dans certains pays, il s’agit de la deuxi`eme loi du mouvement d’Euler qui vient
compl´eter la premi`ere, vue au chapitre pr´ec´edent.
Dans ce chapitre, nous limiterons son application `a l’´etude des solides en rotation autour d’un axe fixe. Les
mouvements plus g´en´eraux seront ´etudi´es par la suite.
3.2.4 Calcul du moment cin´etique dans le cas d’une rotation autour d’un axe fixe
Ce qui nous int´eresse souvent lors de l’´etude du mouvement de rotation d’un solide, ce n’est pas de connaˆıtre
son moment cin´etique, mais plutˆot sa vitesse de rotation caract´eris´ee par le vecteur ~! . Comment relier ~ oet ~! ?
Le lien entre ~ oet ~! n’est, a priori, pas simple et se fait g´en´eralement `a l’aide d’une relation matricielle.
Mais, dans le cas d’une rotation autour d’un axe fixe, on peut simplifier le probl`eme. Pour r´esoudre l’´equation
di↵´erentielle qui r´esulte de l’application du th´eor`eme du moment cin´etique, on la projette sur des axes judi-
cieusement choisis, comme en m´ecanique du point. Il se trouve que la projection sur l’axe de rotation permet
d’acc´eder `a la vitesse ~! . C’est donc ce que nous allons faire.
Chaque point Mdu solide tourne autour de D, sa projection sur l’axe de rotation , et non O. Voir figure
3.1. Il est donc plus simple de faire intervenir Dgrˆace `a une relation de Chasles,
~ o=ZZZS
!
OM ^~v(M)dm =ZZZS
!
OD ^~v(M)dm +ZZZS
!
DM ^~v(M)dm. (3.8)
En remarquant que le premier terme est orthogonal `a ! OD et donc `a l’axe , on a finalement,
~ o·~u=~ ·~u,(3.9)
avec ~u, vecteur unitaire port´e par l’axe de rotation et orient´e suivant le sens positif de rotation.
On d´efinit ~ , le moment cin´etique par rapport `a l’axe de rotation ,
~ =ZZZS
!
DM ^~v(M)dm. (3.10)
Cette expression fait intervenir la vitesse ~v(M) qui d´epend du point Mchoisi. Nous allons donc introduire la
vitesse angulaire ~! qui commune `a tous les points du solide. Pour un mouvement de rotation simple,
~v(M)=~! ^! DM. (3.11)
Alors,
~ =ZZZS
!
DM ^(~! ^! DM)dm. (3.12)
En utilisant la formule du double produit vectoriel, ~a^(~ b^~c)=(~a . ~c )~ b(~a . ~ b)~c, on obtient,
~ =ZZZS (! DM)2~! d m ZZZS (! DM.~!)! DM dm. (3.13)

CHAPITRE 3. ROTATION AUTOUR D’UN AXE FIXE 26
Le deuxi`eme terme de l’´equation pr´ec´edente est nul car ! DM ?~! . Finalement, on a,
~ =✓ZZZS DM2dm◆~! =I~! .(3.14)
On a r´eussi `a ´etablir un lien direct entre le moment cin´etique par rapport `a l’axe de rotation, ~ et la vitesse de
rotation ~! . L’int´egrale qui relie ces deux grandeurs, et qu’il nous reste `a d´eterminer, RRRSDM2dm,ned´epend
pas du mouvement, seulement des caract´eristiques du solide.
On d´efinit I,moment d’inertie du solide par rapport `a l’axe , comme
I=ZZZS DM2dm. (3.15)
Cette int´egrale ne peut pas s’annuler. On se penchera plus tard sur les moments d’inertie, section 3.5. Revenons
au moment cin´etique.
On peut conclure de ce calcul complexe, que l’on a simplement
~ =I·~! .(3.16)
Cette expression du moment cin´etique est `a rapprocher de celle de la quantit´e de mouvement pour comprendre
l’importance du moment d’inertie. Il joue le mˆeme rˆole que la masse d’inertie, mais tient compte de l’´eloignement
`a l’axe.
3.2.5 Conclusion
Pour un solide en rotation autour d’un axe fixe, l’application du th´eor`eme du moment cin´etique
conduit `a
I˙!=⇣X! OAi^~ Fi⌘·~u.(3.17)
o`u ~ Fisont les forces ext´erieures appliqu´ees au solide, Aileur point d’application, Oest un point
de l’axe, ~ule vecteur unitaire port´e par l’axe, orient´e suivant le sens de rotation choisi, I,le
moment d’inertie du solide par rapport `a cet axe et !, la vitesse angulaire de rotation du solide
autour de cet axe.
On aboutit `a une ´equation di↵´erentielle simple qui ressemble `a celles vues lors de l’´etude du mouvement des
points.
Pour des mouvements plus complexes, o`u il n’y a pas d’axe de rotation fixe, l’´equation `a ´etudier n’est pas
la mˆeme. On verra cela dans le chapitre suivant.
3.3 Aspect ´energ´etique
3.3.1 Calcul de l’´energie cin´etique pour un solide en rotation autour d’un axe fixe
L’´energie cin´etique d’un solide en mouvement est d´efinie par
Ec =ZZZS v2(M)dm. (3.18)
Dans le cas d’un solide en rotation, nous allons utiliser le vecteur rotation angulaire ~! et introduire D,la
projection du point Msur l’axe , afin de calculer plus facilement la norme de ~v(M),
~v(M)=~! ^! DM, (3.19)
et donc,
k~v(M)k=k~! k·k
!
DMk,car ~! ?! DM. (3.20)
Finalement,
Ec =1
2✓ZZZS
DM2dm◆!2.(3.21)

CHAPITRE 3. ROTATION AUTOUR D’UN AXE FIXE 27
On reconnaˆıt le moment d’inertie. Et donc, finalement, on a simplement,
Ec =1
2I!2.(3.22)
Comme le moment cin´etique, l’´energie cin´etique d’un mouvement de rotation fait intervenir le moment d’inertie
et la vitesse angulaire. On retrouve le rˆole important du moment d’inertie.
3.3.2 Th´eor`eme de l’´energie cin´etique pour un solide en rotation autour d’un axe
fixe
Le th´eor`eme de l’´energie cin´etique vu en m´ecanique du point peut ˆetre ais´ement g´en´eralis´e au cas d’un solide
en rotation. En notant ~ Files forces ext´erieures s’appliquant en un point Aidu solide, le travail ´el´ementaire des
forces ex´erieures vaut,
W=X
i
~
Fi.~v(Ai)dt =X
i
~
Fi.(~! ^! OAi)dt. (3.23)
L’expression en fonction du vecteur rotation ~! n’est valable que pour un mouvement de rotation autour d’un
axe fixe passant par O.
En utilisant les propri´et´es du produit mixte,
W=(
X
i
!
OAi^~ Fi).~! dt =X
i
~
M~
Fi/O.~! dt. (3.24)
En m´ecanique du point, le travail des forces ext´erieures est ´egal `a la variation de l’´energie cin´etique. C’est encore
vrai en m´ecanique du solide et nous allons le d´emontrer `a l’aide du th´eor`eme du moment cin´etique.
W=d~o
dt .~! dt =d dt .!dt =I
d!
dt !dt=dEc. (3.25)
En conclusion, pour un solide en rotation autour d’un axe fixe, l’´energie cin´etique s’´ecrit
Ec =1
2I!2et sa variation est ´egale au travail des forces ext´erieures qui peut s’exprimer ainsi,
pour un d´eplacement ´el´ementaire :
dEc =W=X
i
~
M~
Fi/O.~! dt. (3.26)
Nous verrons au semestre suivant une expression plus g´en´erale pour tous les mouvements.
3.4 Comparaison avec la m´ecanique du point
Point mat´eriel Solide en rotation autour d’un axe fixe
Mouvement ~v(M)~!
Etude du d~p
dt =P~
Fext d~o
dt =P~
M~
Fext /O
mouvement avec ~p=m~vavec ~ o.~u=I!
Th´eor`eme de dEc =P~ Fext.~vdt dEc =P~ M~
Fext /O.~!dt
l’´energie cin´etique avec Ec =1
2mv2avec Ec =1 2I!2
Le mouvement d’un point mat´eriel est caract´eris´e par sa vitesse ~v(M) et d´epend des actions du milieu ext´erieur
(la r´esultante des forces ext´erieures) et de la “r´epugnance” du point `a voir son mouvement modifi´e, c’est `a dire,
sa masse d’inertie. Le mouvement d’un solide en rotation autour d’un axe fixe, est caract´eris´e, quant `a lui, par
sa vitesse angulaire ~! et il faut remplacer la quantit´e de mouvement et la r´esultante des forces par leur moment
respectif par rapport `a un point fixe.
Ce tableau contient toutes les relations `a connaˆıtre et `a savoir utiliser.
Pour un solide en rotation autour d’un axe fixe, ce qui caract´erise le syst`eme ´etudi´e, ce n’est plus la masse
d’inertie, mais le moment d’inertie par rapport `a l’axe de rotation. Nous allons donc apprendre `a calculer cette
nouvelle grandeur.