Projet d`algorithmique

Page 1 / 1
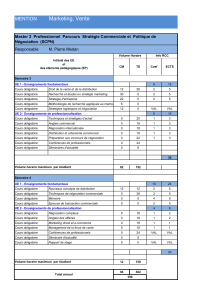
CARRIERE Sébastien
MÉRÉ Aurélien
P
Pr ro oj je et t d d’ ’a al lg go or ri it th hm mi iq qu ue e

Page 2 / 2
Sommaire
S
So om mm ma ai ir re e. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .2 2
P
Pr re em mi iè èr re e p pa ar rt ti ie e. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .3 3
I
In nt tr ro od du uc ct ti io on n. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .4 4
A
Al lg go or ri it th hm me e d de e r re ec ch he er rc ch he e s sé éq qu ue en nt ti ie el ll le e. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .4 4
Introduction ...................................................................................4
Algorithme.....................................................................................4
Analyse de complexité........................................................................5
Jeux d’essais ..................................................................................5
Autres essais pratiques et avantages.........................................................5
A
Al lg go or ri it th hm me e d de e t to ou ur rn no oi i. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .6 6
Introduction ...................................................................................6
Réflexions préliminaires ......................................................................6
Principe pratique..............................................................................6
Algorithme.....................................................................................7
Complexité ....................................................................................7
C
Co on nc cl lu us si io on n. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .9 9
D
De eu ux xi iè èm me e p pa ar rt ti ie e. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 10 0
I
In nt tr ro od du uc ct ti io on n. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 11 1
P
Pr ri in nc ci ip pe e d du u t tr ri i t to ou ur rn no oi i. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 11 1
L
La a s st tr ru uc ct tu ur re e d de e d do on nn né ée es s. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 11 1
L
L’ ’a al lg go or ri it th hm me e. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 12 2
L
La a c co om mp pl le ex xi it té é. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 14 4
Complexité en temps ....................................................................... 14
Complexité en espace....................................................................... 14
L
Le es s j je eu ux x d de e t te es st ts s. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 15 5
C
Co om mp pa ar ra ai is so on n a av ve ec c l le e p pr ri in nc ci ip pe e 1 1. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 17 7
C
Co od de e s so ou ur rc ce e d du u p pr ro og gr ra am mm me e f fi in na al l. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. .1 17 7

Page 3 / 3
Première partie

Page 4 / 4
Introduction
Le but de ce projet est de réaliser un algorithme de recherche des deux plus grands
éléments d’une liste. Nous étudierons dans ce dossier d’une part un algorithme de
recherche séquentielle, et un algorithme de tournoi.
Algorithme de recherche séquentielle
Introduction
L’algorithme de recherche séquentielle balaye séquentiellement la liste de n éléments
jusqu’à trouver les deux plus grands éléments. Deux balayages sont effectués : le premier pour
détecter le maximum de la liste, et le deuxième pour déterminer le second maximum. Avant le
deuxième balayage, on aura pris sans de retirer de la liste le maximum précédemment trouvé afin
d’éviter sa réplication.
Tous les algorithmes présentés ci-après supposent que la liste contient au moins 2 éléments.
Nous présenterons cet algorithme avec une liste de type tableau. Nous aurions également pu
utiliser une liste chaînée : il n’y a strictement aucun changement, si ce n’est dans la méthode de
balayage. Toutefois, la complexité reste inchangée si on se base sur le nombre de comparaisons.
Algorithme
Procedure Recherche2Max_Seq (tableau t(1..n) entiers)
/* Recherche séquentiellement les deux maximum du tableau t */
/* max1 et max2 contiennent les maximum
i est un index de boucle
pmax est l'indice de la valeur maximum du tableau */
Entier max1, max2, i, pmax;
/* Premier balayage */
i=2;
pmax=1;
Tant Que (i<n)
Si (t[i] > t[pmax]) Alors
pmax=i;
Fin Si
Fin Tant Que
/* Deuxième balayage */
max1=t[pmax];
t[pmax]=t[1];
max2=t[2];
i=3;
Tant Que (i<n) faire
Si (t[i] > max2) alors
max2 = t[i];
Fin Si
Fin Tant Que
t[pmax]=max1;
Fin

Page 5 / 5
Analyse de complexité
On prendra comme opération fondamentale la comparaison entre éléments dans notre
analyse. Comme nous pouvons le voir dans le programme, il n’y a que deux instructions de
comparaisons, chacune dans l’enceinte d’une boucle.
La première : « Si (t[i] > t[pmax]) Alors » est réalisée pour n variant de 2 à n.
La seconde : « Si (t[i] > max2) alors » est réalisée pour n variant de 3 à n.
En conséquence, la complexité théorique sera :
?? ?? ??????? n
i
n
innn 32 32)2()1(11
Jeux d’essais
Examinons le jeu d’essai suivant (tableau de 10 éléments) :
Avant le premier balayage, les variables sont initialisées aux valeur suivantes :
On compare Pmax à tous éléments du tableau entre i et n, soit 9 comparaisons (On a surligné
les éléments qui ont été comparés). Après le premier balayage, les variables contiennent les valeurs
suivantes :
Avant le deuxième balayage, le tableau a été réinitialisé, de même que la variable i :
On compare Pmax à tous éléments du tableau entre i et n, soit 8 comparaisons (On a surligné
les éléments qui ont été comparés). Après le second balayage, les variables contiennent les valeurs
suivantes :
Après le second balayage, les valeurs initiales du tableau sont rétablies. Le nombre de
comparaisons totales est donc de 9+8=17 comparaisons. Comme nous disposions de 10 éléments
dans notre tableau, nous trouvons donc bien pratiquement 2n-3=17 comparaisons.
Autres essais pratiques et avantages
Pratiquement, sur un tableau de 1 million d’éléments de type entiers longs choisis au hasard,
on trouve 1999997 comparaisons, ce qui correspond une fois de plus au résultat théorique.
L’avantage de cet algorithme est qu’il n’occupe aucun espace mémoire supplémentaire de celui
alloué pour la liste. Il faut toutefois que celle-ci soit en lecture/écriture pour fonctionner
correctement. Pour pallier également à son manque de rapidité, nous allons voir le tri tournoi.
10
4
8
12
2
6
3
18
16
1
10
4
8
12
2
6
3
18
16
1
Pmax=1 i=2
10
4
8
12
2
6
3
18
16
1
Pmax=8
Max1=18
10
4
8
12
2
6
3
10
16
1
Max2=4 I=3 T[10]=T[1]
10
4
8
12
2
6
3
10
16
1
Max2=16