Problèmes de courant continu - Jean

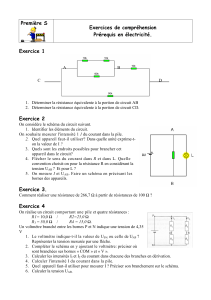
Problèmes de courant continu
I. Capteur résistif de température.
Variation de la résistance d’une thermistance en fonction de la température.
La résistance d’une thermistance, formée d’un matériau semi-conducteur, varie avec la température absolue T
suivant la loi
R
00
exp BB RR TT
⎛⎞
⎟
⎜
=−⎟
⎜⎟
⎟
⎜
⎜
⎝⎠
où B, R0 = 12000 Ω et T0 = 298 K sont des constantes.
1) Que représente la constante R0 ?
2) Exprimer le coefficient de température 1dR
RdT
α= en fonction de B et T.
3) Calculer B sachant que α (T = 298 K) = – 4,135.10–2 K–1.
4) Calculer R aux températures 0 °C et 100 °C.
5) Le coefficient de dilatation linéaire du semi-conducteur est 5
110 K d
dT
λ−−
==
A
A
1
. Comparer les variations de
résistance avec la température dues à la variation de la résistivité ρ d'une part et aux variations de dimensions d'autre
part. Conclure.
Pour mesurer une température, on utilise un capteur résistif. On mesure un signal électrique, en général une
tension, qui traduit les variations de la résistance avec la température. Un montage, alimenté par une source de tension
comprend la résistance à mesurer et d'autres résistances constantes. Le circuit de mesure ainsi constitué est appelé
conditionneur du thermomètre.
v1R
d
R
R1 – r
e
r
Montage potentiométrique.
Celui-ci est représenté sur la figure ci-contre. Le générateur a pour fem e
et pour résistance interne r ; le voltmètre de résistance interne Rd mesure la
tension aux bornes de la résistance thermométrique R qui dépend de T.
1
v
6) Exprimer en fonction de R
1
v1, R, Rd, et e.
7) Comment doit-on choisir Rd pour que la tension ne dépende pas
trop du voltmètre utilisé ? Quelle est alors l’expression de ? On suppose
cette condition désormais réalisée.
1
v
1
v
source voltmètre
8) À T = T0, la résistance thermométrique R a pour valeur R0 et la tension de mesure la valeur . Ces conditions
définissent un point moyen de fonctionnement. Lorsque R varie de ∆R, varie de . Exprimer en fonction
de ∆R, Ro, R
1
v
1
v1 v∆1 v∆
1 et e, en se limitant au cas où .
0
RR∆
9) On définit la sensibilité du conditionneur par 1
v
SR
∆
=∆. Pour quelle valeur de R1, cette sensibilité est-elle
maximale au voisinage de T = T0 ? Calculer cette sensibilité maximale.
Application numérique. Sachant que e = 10,0 V, R0 = 109,8 Ω, r = 20 Ω, que le voltmètre peut déceler une variation
1
v∆ de 0,01 volt, calculer la valeur de R1 – r qui donne la sensibilité maximale et la valeur ∆R que l'on peut alors tout
juste déceler.
10) Alors que le conditionneur a sa sensibilité maximale, la fem e du générateur fluctue entre e – ∆e et e + ∆e.
Calculer la variation de correspondant à une variation ∆e de e. Comparer l'influence de ∆R et de ∆e. Quel est le
niveau tolérable de fluctuations de la fem de la source dans ce dispositif ?
1
v
e
Pont de Wheatstone.
Le voltmètre V, de résistance interne Rd très supérieure aux autres résistances,
mesure la d.d.p. v2 = vB – vA. La résistance interne de la source est négligeable
(figure 2).
C
B
A
R4 R3
R2
R(T)
V
11) Exprimer v2 en fonction de e et des résistances
12) L'équilibre du pont (v2 = 0) est réalisé pour R = R0, T = T0. Quelle relation
lie alors R2, R3, R4, et Ro ?
13) Calculer v2 en fonction de R, R2, R0 et e.
14) On suppose ∆R = R – R0 << R0. Pour quelle valeur de R2 la sensibilité
est-elle maximale ? Calculer celle-ci.
2/Sv R=∆
D
15) Comparer la sensibilité du pont de Wheatstone et du montage
potentiométrique dans les deux cas :
- le voltmètre n’est utilisé que sur le calibre immédiatement supérieur à e ;
- on peut aussi utiliser des calibres plus petits.
DS : problèmes de courant continu, page 1 Figure 2

16) La sensibilité maximale étant obtenue, on tient maintenant compte des fluctuations ∆e de e (|∆e| << e). Comparer
l’influence respective de ∆R et de ∆e sur v2. Conclure.
II34. Pont de Wheatstone.
0. Préliminaire : montrer que 2
()
ydx xdy
x
dxy xy
−
⎛⎞
⎟
⎜=
⎟
⎜⎟
⎜
⎝⎠
++
.
1. Une jauge de contrainte J1est constituée par un fil cylindrique de
longueur l, de section
s
et de résistivité
ρ
. Elle est collée
longitudinalement sur une poutre isolante fixée par son extrémité
inférieure (fig. 1). Lorsque la poutre est rectiligne, la résistance du
fil est . Sous l'action d'une force
1
R
F
horizontale, l'extrémité libre
B de la poutre fléchit et la poutre se courbe. La température étant
constante, le fil subit un très faible allongement relatif
l
l
∆
= ε
. Il en
résulte une très faible variation de résistance ll
K
R
R∆
=
∆
1
1. Au cours
de la déformation, les variations relatives de la section s et de la
résistivité
ρ
sont respectivement
l
l
s
s
∆
−=
∆
σ 2 et V
V
c
∆
=
∆
ρ
ρ
,
σ
et étant deux constantes dépendant de la
nature du conducteur et V son volume. Exprimer le coefficient
c
K
en fonction de c et
σ
.
Fi
gu
r
e
1
Application numérique : ,
13,1=c3,0=
σ
; calculer
K
. En déduire la variation de résistance pour une
force
1
R∆
F
exercée de , sachant que N10 FK
l
l1
=
∆ (avec ) et que
15
1N10 −−
=KΩ350
1
=
R lorsque le fil est au
repos.
2. Le fil cylindrique précédent constitue l'une des branches d'un pont de Wheatstone (fig. 2). Les résistances
sont tout d'abord considérées comme constantes. Seule varie en fonction de la force appliquée.
Entre les bornes de sortie A et C du pont est placé un appareil de mesure (M) de résistance interne infinie. Ce
pont est alimenté par un générateur de f.e.m.
432 ,, RRR 1
R
E
constante et de
résistance interne négligeable.
Figure 2
2.a. Exprimer la différence de potentiel CAAC VVU
−
=
en
fonction de .
4321 ,,,, RRRRE
2.b. On suppose qu’initialement RRRRR
=
=
== 4321 ;
variant d'une quantité très petite devant , exprimer la
variation correspondante . Calculer numériquement
1
R
1
R∆1 R
AC
U∆AC U
∆
si , et V2=EΩ1,0
1=∆RΩ350
=
R.
3. Afin d'améliorer la sensibilité du dispositif, c'est-à-dire
d'obtenir une différence de potentiel entre A et C plus im
en fonction de la force appliquée, on dispose de 4 jauges
identiques J
portante
,RR .
3.a. Initialeme . En supposant que la
placé entre A et C est
1, J2, J3, J4 de résistances respectives 21 ,, RR
nt
43
RRRRR ==== 4321
résistance de (M) infinie, exprimer la
d.d.p. AC
U∆ en fonction de 4321 ,,,, RRRRE
∆
∆∆∆ et R.
3.b. Pré comment il faut co la po treciser ller les 4 jauges sur u pour que le dispositif soit le plus sensible.
Ω1,0
4321 ∆=∆=∆=∆ RRRR
3.c. Calculer numériquement dans l’hypothèse précédente AC
U
∆
si V2
=
E, = et
4. On utili résistances qu’on croit égales , mais en réalité elles sont
on intervertit les jauges J et J2 ;
en
e
Ω350=R.
se des 1234 1000RRRRR===== Ω
légèrement différentes. Le pont étant équilibré, 1pour rétablir l’équilibre du
pont, il faut mettre en série avec 3
R une résistance additionnelle 6r=Ω. Montrer que 12 RR≠. Exprimer
fonction de r et calculer RR−t RR−.
12
34

III17.
Une locomotive électrique est alimentée en courant continu.
L'alimentation est réalisée par des sous-stations Si distantes de L. Ces
sous-stations relient les rails FG, portés au potentiel nul, à la caténaire AB,
c’est-à-dire à un fil électrique situé au dessus de la locomotive sur lequel
vient frotter son pantographe. Chaque source Si sera représentée par une
source de tension de force électromotrice E, la borne positive étant du côté
de la caténaire.
La motrice M est branchée entre les rails et le contact C entre le
pantographe et la caténaire. On supposera que son moteur doit être
alimenté par un courant constant I. La motrice peut donc être schématisée
par une source de courant de courant électromoteur I = 800 A. De plus la
caténaire présente une résistance linéique (rapport de la résistance à la
longueur) de valeur r = 5.10–5 Ω.m–1 , alors que la résistance des rails est
négligeable.
1) On considère une section de ligne de longueur L alimentée par deux
sous-stations. On note x = AC la longueur de caténaire séparant la motrice
de la sous-station S1 et U la tension aux bornes de la motrice.
Exprimer la chute de tension ∆U = E – U en fonction de E, r, x, L et I.
Déterminer la limitation sur la distance L entre les deux sous-stations pour
que ∆U ne dépasse pas ∆UM = 45 V.
2) Une section de longueur L est maintenant alimentée par une seule
station S située à son extrémité. La caténaire est constituée de deux fils
identiques AB et A'B' de longueurs L et de résistances linéiques r, reliés à
leurs extrémités. Le pantographe n’est en contact qu’avec un des deux fils..
Exprimer de nouveau ∆U = E – U en fonction des données et calculer la
valeur maximale de la distance L pour limiter la chute de tension à ∆UM =
45 V.
3) On revient à un système de deux stations S1 et S2, mais avec une caténaire à deux fils connectés par leurs
extrémités et leur milieu. Le pantographe n’est en contact qu’avec un des deux fils.
Exprimer ∆U = E – U en fonction des données et calculer, comme précédemment, la valeur maximale de L.
4) Conclusion : quel est le montage le plus avantageux ?
5) Comment traiter la configuration de la première question si la résistance des rails n’est pas négligeable ?
Réponses
I ; 1) valeur de R à ; 2) ; 3) ; 4) ; ;
0
T2 /BTα=−3672 KB=
()
0 C 37 089R°= Ω
()
100 C 1007R°= Ω
5) la variation de la résistance est due essentiellement à la variation de la résistivité ;
6)
()
11
11/1/
d
e
vRR R
=++ ; 7) ;
d
RR11
eR
vRR
=+ ; 8)
()
11
2
1
veR
SRRR
∆
=≈
∆+ ; 9) ;
10
RR=
0
4
M
e
SR
= ; ;
189, 8Rr−=Ω10, 44
M
v
RS
∆
∆==Ω ; 10) à sensibilité est maximale, , donc
; doit être inférieur à 0,02 V ; 11)
1/2ve=
1/2ve∆=∆e∆
()
()
()
2243
11
1/1/
BvAe RRT RR
⎛⎞
⎟
⎜
=−=−⎟
⎜⎟
⎜
⎝++⎠
vv ; 12)
2
03
RR
RR
=4
; 13) 222
11
1/1/
0
RR RR
⎛⎞
⎟
⎜
=−⎟
⎜⎟
⎜
⎝++⎠
ve ; 14) ;
20
RR=
0
4
M
e
S ; 16)
R
=204
Re
vR
∆∆
∆ . =
II. 1) ; 2.a)
111
( 1) 2 ( 1) 2,05 0,07Kc c RRKKF=+−−=∆==Ωσ
12
1423
AC
RR
UE
RRRR
⎡⎤
=−
⎢⎥
++
⎢⎥
⎣⎦
; 2.b) 14
1, 4.10 V
4
AC
ER
UR
−
∆
∆== ; 3.a)
134
(
4
AC
ERRRR
UR
∆+∆−∆−∆
∆=2
)
; 3.b) coller J1 et J3 du coté où la poutre est en
extension et J2 et J4 du coté où la poutre est en compression ; 3.c) 4
5, 7.10 V
AC
U− ∆= ;
4) ;RR .
12 /2 3RR r−=Ω34 /2 3
E
E I
x
S1M
L
x
S1S2
E I
M
L
Question 3
Question 2
I
E S1S2
E
M
L
x
A B
C
Question 1
FG
J1
J3
J2
J4
r−−=−Ω
III. 1)
()
rIx L x
UL
−
∆ ; =44500 m
M
U
LrI
∆
<=
; 2)
()
2
2
xL xrI
UL
−
∆= ; L ; 3) 2250 m<
()
23
2
LxxrI
UL
−
∆= ; 66750 m
M
U
L ; 4) la configuration 1 est préférable ; 5) considérer rr .
rI
∆
<= r=+
12

Corrigés
I.
1) représente la valeur de à .
0
R R 0 TT=
2) 00
ln ln BB
RR
TT
=+− ; en dérivant cette relation par rapport à T : 2
1dR B
RdT T
α==−.
3) .
222
4,135 10 298 3672 KBT − =−α =××=
4)
()
3 672 3 672
0 C 12 000 exp 37 089
273 298
R⎛⎞
⎟
⎜⎟
°= −=Ω
⎜⎟
⎜⎟
⎜
⎝⎠
;
()
3672 3672
100 C 12 000 exp 1007
373 298
R⎛⎞
⎟
⎜⎟
°= −=Ω
⎜⎟
⎜⎟
⎜
⎝⎠
.
5) L
RS =ρ ; d'où : ln ln ln lndR d dL dS
dT dT dT dT
ρ
=+−.
Si la dilatation est isotrope, ln ln
22
dS dL
dT dT
==λ, soit lnd
dT
ρ
α=−λ.
Comme et , la variation de la résistance est due essentiellement à la variation de la résistivité,
la variation des dimensions produisant un effet négligeable.
2
4.10− α≈− 5 10− λ=
6) C'est un montage diviseur de tension : le même courant parcourt et . D'où :
()
1
rRr+−d RR&
1
1dd
ev
RRR RR
=
+&&
, soit 111
11
11
dd
ee
vRR
RR RR
==
⎛⎞
⎟
⎜
+++
⎟
⎜⎟
⎜
⎝⎠
&
.
7) ne dépend pas de si , ce qui est assez facilement réalisé. Alors
1
vd Rd RR111
1
eeR
vRRR
R
==
+
+
.
8) En dérivant la relation précédente, on obtient
()
11
2
1
dv eR
dR RR
=+.
En assimilant les petites variations à des différentielles :
()
11
2
1
veR
SRRR
∆
=≈
∆+.
9) 2
01 0 1
/2
e
SRR R R =++
est maximum quand est minimum ; or il s'agit de la somme de deux
nombres de produit déterminé ; cette somme est minimum quand les deux termes sont égaux, soit quand .
2
01
/RR R+1
2
0
R10 RR=
La sensibilité maximale est alors
0
4
M
e
SR =.
AN : ; .
189, 8Rr−=Ω0, 0229 V/ M
S=Ω
On détecte tout juste 10, 01 0, 44
0, 0229
M
v
RS
∆
∆== =Ω.
10) Dans des conditions quelconques, 11
Re
vRR
∆
∆=+. Si la sensibilité est maximale, , donc .
1/2ve=1/2ve∆=∆
e∆ doit être inférieur à 0,02 V pour que n'excède pas 0,01 V et n'influence pas la mesure. Il faut donc une tension
d'alimentation très stable pour faire des mesures valables.
1
v∆
11) Les branches d'une part, d'autre part, sont des diviseurs de tension :
()
2
,RT R 34 ,RR
()
()
() ()
()
()
()
2
21
vC vA e e
vC vA R
RT RT R
RT
−=⇒−=
++
;
() () () ()
4
334
3
1
vC vB e e
vC vB R
RRR
R
−=⇒−=
++
.
En retranchant membre à membre, il vient :
()
()
()
224
3
11
11
vvBvAe RR
RT R
⎛⎞
⎟
⎜
=−=−⎟
⎜⎟
⎜⎟
⎜++
⎟
⎜⎟
⎜⎟
⎝⎠
.
12) est nul si
2
v24
03
RR
RR
=.
13) 222
0
11
11
ve RR
RR
⎛⎞
⎟
⎜
=−⎟
⎜⎟
⎜⎟
⎜++
⎟
⎜⎟
⎜⎟
⎝⎠

14) En dérivant la relation précédente, on obtient
()
22
2
2
dv eR
SdR RR
==
+ qui est semblable à la relation trouvée dans
la question 8. La sensibilité est donc maximale pour et vaut alors
2
RR=00
4
e
R.
15) Avec un seul calibre, les deux méthodes ont même sensibilité. Si des calibres nettement inférieurs à e sont
disponibles, le pont de Wheastone permet de les utiliser, car à l'équilibre est nul ; le capteur est alors plus sensible
2
v
monté sur un pont de Wheatstone que sur un montage potentiométrique.
16) De la relation de 13), on déduit
()
()( )
02
200 2
eR R R
v, d'où
RRR R
−
=++ 204
Re
vR
∆∆
∆. L'influence des fluctuations de
est beaucoup plus faible que dans le cas du montage potentiométrique si ∆ est petit.
=
e R
II. Pont de Wheatstone.
0. En utilisant
()
2
vdu udv
u
d, on obtient :
vv
−
=22
() ( )
() ()
x y dx x dx dy y dx x dy
x
d.
xy xy xy
+−+−
⎛⎞
⎟
⎜==
⎟
⎜⎟
⎜
⎝⎠
++ +
1.
()
1
1
1
(ln ) (ln ln ln )
dR d dlds dV dlds dlds dlds
dR d l s c c
RlsVls
ρ
ρρ
==+−=+−=+−=++−
lsls
Comme Vl, s=dV et
dl ds
Vls
=+
1
1
5
111
( 1) ( 1) [( 1) 2 ( 1)]
( 1) 2 ( 1) 2,13 2 0,3 0,13 2,05
350 2,05 10 10 0,07
dR dl ds dl
cc cc
Rls
Kc c
RRKKF
σ
σ
−
=+ +−=+−−
=+−−=−×× =
∆==×××=Ω
l
=E=
2. a. Supposons VN ; alors VP . Appliquons le
théorème de Millman aux points A et C :
() 0 ()
41 3
14 2
14 23
12
1423
() ()
11 11
AC
EE
RER RER
VA VC
RR RR
RR RR
RR
UE
RRRR
== ==
++
++
⎡⎤
⎢⎥
=−
⎢⎥
++
⎣⎦
2
3
2.b. La relation du préliminaire montre que
41 14
2
14
20,1 1, 4.10 V
( ) 4 4 350
AC AC
RdR ER
dU E U
RR R
−
∆×
=∆== =
+×
. F
3.a. En utilisant la relation du préliminaire,
41 14 32 23
22
14 23
1342
() ()
()
4
AC
AC
R dR R dR R dR R dR
dU E RR RR
ERRRR
UR
−−
⎡⎤
⎢⎥
=−
⎢⎥
++
⎣⎦
∆+∆−∆−∆
∆=
J1
J3
J2
J4
igure 2
3.b. Il faut coller J1 et J3 du coté où la poutre est en extension et J2 et J4 du coté où la poutre
est en compression.
3.c. La tension est le quadruple de celle de la question 2.b : 4
5, 7.10 V
AC
U− ∆=.
4. Les deux équilibres impliquent 142 4
2313
RRR R
RRRR
==
+r
Le quotient membre à membre donne :
2
13
23
RR
RR
r+
⎟=
⎟
⎟
⎟
⎝⎠ ≠
⎛⎞
⎜
⎜
⎜ qui montre que RR ;
12
12
12
233 3
11
222
Rrr rRr
RR
RRR R
=+ + −==Ω3
On en tire 41
34
32 3
13
22
RR r r
RR
RR R
=+ −−=−Ω
III.