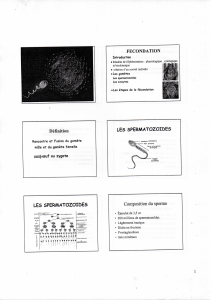
Actions mécaniques de la lumière. Principes et Applications

105106
P=N.kB.T = 2Nm < u2
z>
2
m N
< u2
z>
0z
P=Np< u2
z>
2.2mq< u2
z>

I
δ²
I=Np< u2
z>
2.δ²
δ² =m.uδu =1
3m.uzδuz
δpz=m.δuz
δP =Np< u2
z>
2.m.δuz=Np< u2
z>
2.3I
uz.Np< u2
z>/2
δP =3I
uz
uz
Oz
I/c
Pradiometrique ∼Pradiation.c
u
c/u