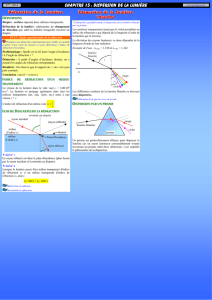
déviation de la lumière par un prisme

Lydie GERMAIN 2
nde
- U3 - Page 1/2 21/10/2010
2
nde
DÉVIATION DE LA LUMIÈRE PAR UN PRISME
U3-P3
Objectifs :
• Pratiquer une démarche expérimentale pour établir un modèle à partir d’une série de mesures et pour
déterminer l’indice de réfraction d’un milieu.
• Interpréter qualitativement la dispersion de la lumière blanche par un prisme.
On a vu précédemment que lorsque la lumière blanche passe à travers un prisme, elle est décomposée et elle
ne se propage pas en ligne droite.
1. Propagation de la lumière
La lumière se propage en ligne droite dans un milieu homogène et transparent.
2. Passage de la lumière d’un milieu homogène à un autre
 Passage de la lumière d’un milieu transparent à un autre.
Lorsque la lumière passe de l’eau à l’air ou de l’air à l’eau, elle est déviée.
 Définition.
La réfraction de la lumière est le changement de direction de propagation que subit un rayon lumineux
lorsqu’il traverse la surface de séparation entre deux milieux de propagation.
Si le milieu n’est pas homogène, la lumière ne se propage plus en ligne droite, c’est le cas des mirages. Il y a
réfraction de la lumière.
3. La réfraction
3.1. Vocabulaire
On appelle :
 Dioptre : la surface séparant deux milieux transparents différents.
 Point d’incidence : le point d’intersection entre le rayon incident et le dioptre.
 Normale (ou droite normale) : la droite perpendiculaire à la surface et passant par le point d’incidence.
 Angle d’incidence : l’angle
1
i
ɵ
entre la normale et le rayon incident.
 Angle de réfraction : l’angle
2
i
ɵ
entre la normale et le rayon réfracté.
 Plan d’incidence : le plan contenant le rayon incident et la normale.
rayon incident
rayon réfracté
normale
milieu transparent 1
milieu transparent 2
1
ˆ
i
Surface de
séparation
2
ˆ
i
miroir
eau + fluoresceïne

Lydie GERMAIN 2
nde
- U3 - Page 2/2 21/10/2010
3.2. Lois de Snell-Descartes
1° loi:
Le rayon incident, le rayon réfracté et la normale à la surface de séparation au pont d’incidence sont dans la
même plan, appelé le plan d’incidence.
2° loi :
Lorsqu’un rayon lumineux passe d’un milieu transparent 1 un milieu transparent 2, on a
1 1 2 2
n sin i n sini
=
Avec
1
n
l’indice de réfraction du milieu 1 et
2
n
l’indice de réfraction du milieu 2, grandeur sans unité.
Pour l’air,
air
n 1,00
=, l’indice des autres milieux est toujours supérieur à 1.
4. Interprétation de la dispersion de la lumière par un prisme
4.1. Indice de réfraction et longueur d’onde
L’indice de réfraction d’un milieu dispersif dépend de la longueur d’onde de la radiation qui le traverse.
L’indice de réfraction du verre diminue quand la longueur d’onde augmente ;
4.2. Effet du prisme sur la lumière blanche
On considère un prisme pour lequel on a :
pour la radiation rouge
R
780 nm
λ = ,
R
n 1,511
=
pour la radiation violette
V
400 nm
λ = ,
V
n 1,531
=
Sur la surface d’entrée, l’angle d’incidence est le même pour toutes les radiations.
On prendra
1
i 30
= °
.
Quand est-il de l’angle de réfraction ?
On a
1 1 2 2
n sin i n sini
= donc
1
2 1
2
n
sini sini
n
=.
Pour la radiation rouge 2R 1,000
sini sin30 0,331
1,511
= = et 2R
i 19,32
= °
Pour la radiation violette 2V 1,000
sini sin30 0,327
1,531
= = et 2V
i 19,06
= °
Les angles de réfraction sont donc différents après la première face.
La deuxième réfraction au niveau de la deuxième face, sépare encore plus les radiations.
Conclusion
Le prisme disperse les lumières polychromatiques car son indice de réfraction dépend de la longueur d’onde
des radiations lumineuses