COMPOSITION DE PHYSIQUE Premier exercice Second exercice

CONCOURS D’ADMISSION 2017 FILIÈRE UNIVERSITAIRE INTERNATIONALE
Seconde voie pour les élèves étrangers francophones
issus de cycles préparatoires des formations françaises à l’étranger
COMPOSITION DE PHYSIQUE
(Durée : 3 heures)
L’épreuve se compose de deux exercices et d’un problème, qui sont indépendants.
L’utilisation des calculatrices n’est pas autorisée.
On se contentera, pour les applications numériques, d’un seul chiffre significatif.
? ? ?
Premier exercice
On dispose de deux lentilles minces convergentes de distances focales f1et f2connues, avec
f2> f1, et d’un banc d’optique permettant d’ajuster leurs positions. Expliquer comment réaliser
une lunette astronomique permettant d’observer des objets situés à l’infini, et déterminer l’ex-
pression de son grandissement. Vous dessinerez un schéma en indiquant la position des lentilles
et de l’oeil de l’observateur.
Second exercice
On dispose de deux résistances R1et R2connues et fixes, d’une résistance ajustable R3, qu’on
peut régler à la valeur qu’on veut, d’un galvanomètre, et d’un générateur. Dessiner le schéma
d’un montage électrique permettant de mesurer la valeur d’une quatrième résistance inconnue
Rx, et justifier précisément son principe.
1

Problème : chute à travers la stratosphère
Données numériques
Accélération de la pesanteur : g= 10 m ·s−2
Constante des gaz parfaits : R= 8 J ·K−1
Capacité thermique de l’eau : CP'CV= 4 ×103J·K−1·kg−1
Le 14 octobre 2012, le parachutiste autrichien Felix Baumgartner est monté à l’altitude de
39000 m à l’aide d’un ballon, et a sauté en chute libre à la verticale jusqu’à l’altitude de 2500 m,
où il a ouvert son parachute. Une balise GPS a permis d’enregistrer sa position au cours de
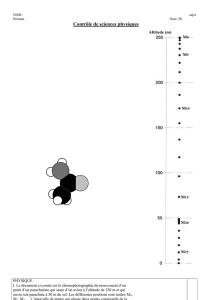
la descente. La figure 1 donne la mesure de sa vitesse vet de son accélération a, toutes deux
comptées positivement vers le bas, en fonction du temps t. La figure 2 donne la mesure de ven
fonction de l’altitude z.
400
vitesse (m/s)accélération (m/s2)
temps (s)
300
200
100
ouverture
du parachute
50 100 150 200 250
(a)
(b)
0
8
4
0
-4
-8
Figure 1 – Vitesse et accélération du parachutiste en fonction du temps.
400
vitesse (m/s)
Altitude (km)
300
200
100
10 20 30 40
0
(c)
ouverture
du parachute
Figure 2 – Vitesse du parachutiste en fonction de l’altitude.
2

1. Représenter ces trois variations dans le cas où la seule force en jeu est la gravité. On indiquera
les valeurs numériques sur les axes de chacun des trois graphiques.
2. La force de résistance de l’atmosphère vaut en valeur absolue F=1
2ρSCxv2, où vest la vitesse
du parachutiste, ρla masse volumique de l’air, Sla surface du parachutiste en projection sur le
plan horizontal, et Cxest appelé “coefficient de traînée”. Déterminer la dimension de Cx.
3. Écrire l’équation du mouvement. On notera mla masse du parachutiste.
4. Estimer, littéralement puis numériquement, la variation relative de l’accélération de la pesan-
teur entre le début et la fin de la chute. Conclure.
5. Sur quelle partie de la trajectoire la force de résistance est-elle négligeable ?
6. Sur quelles parties de la trajectoire l’accélération est-elle négligeable ? Quelle est alors l’ex-
pression de la vitesse ?
7. La masse volumique de l’air en fin de chute vaut environ ρ'1 kg·m−3. Déduire des données
de l’expérience une estimation numérique du rapport m/(SCx). En déduire un ordre de grandeur
de Cx. On supposera dans la suite que le rapport m/(SCx)reste constant au cours de la chute.
8. La vitesse du son dans l’air est donnée par cs=pγP/ρ, où γ= 1,4et Pest la pression.
Vérifier que cette expression est dimensionnellement correcte. On note Pmla pression au point
de la trajectoire où la vitesse est maximale. A quelle condition sur Pmla vitesse en ce point
est-elle supérieure à la vitesse du son ?
Application numérique : La pression à l’altitude z= 28 km vaut 1500 Pa. Qu’en déduit-on ?
9. On se place dans le cadre des hypothèses de la question 6. Ecrire l’expression de l’énergie
dissipée par la force de résistance lorsque le parachutiste descend d’une hauteur h.
10. On suppose que l’énergie dissipée est entièrement absorbée par le parachutiste sous forme
d’énergie interne. Calculer l’ordre de grandeur de sa variation de température lorsqu’il descend
d’un kilomètre, en faisant l’hypothèse que le parachutiste est essentiellement composé d’eau
liquide.
11. On modélise l’atmosphère comme un gaz parfait de masse molaire M= 29 g et de tem-
pérature T0= 290 K à l’équilibre hydrostatique. Exprimer la diminution relative de sa masse
volumique ρsur une petite variation d’altitude δz en fonction des paramètres du problème.
12. Calculer numériquement la diminution relative de ρpar kilomètre d’altitude.
13. Sous les hypothèses de la question 6, en déduire la variation relative de vpar kilomètre
d’altitude. Comparer avec les données de l’expérience.
14. Déduire de l’équation du mouvement de la question 3l’équation différentielle déterminant
la vitesse ven fonction de l’altitude z.
15. En déduire, par un argument dimensionnel, la distance caractéristique Lnécessaire pour
atteindre le régime limite défini à la question 6. Estimer numériquement la valeur de Len fin de
chute. Commenter le résultat.
16. Dans quelle partie de la trajectoire la vitesse est-elle supérieure à la vitesse limite vL, cor-
respondant à une accélération nulle ?
17. Dans le cas où la masse volumique de l’atmosphère est indépendante de z, intégrer l’équation
3

différentielle obtenue à la question 14. On notera z0l’altitude de départ. Tracer l’allure de la
variation de v(z). Vérifier que le résultat obtenu est compatible avec celui de la question 1dans
une limite que l’on précisera. Comparer le résultat avec les données expérimentales.
∗ ∗
∗
4