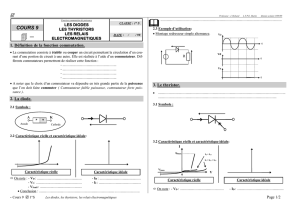
Exemples d`application

1
Exemples d’application
Machine synchrone
Stratégies de commande des machines synchrones
Alimentation Commande Description
Convertisseur de
courant
Onduleur de courant
(commutateur)
DCèAC
Alimentation réseau
Redresseur naturel
ou commandé et
Inductance de
lissage et
Commutateur de
courant
A
B
C
Redresseur
Commutateur de courant
à diode d'isolement
L
Ic
MS
1+2+3+
1-2-3-
Commutation
assistée L’allumage est commandé et
l’extinction est
naturelle
L
Ic
MS
ω
et
120°
1+1- 2+
2-3+2-3-
Ia
b
c
I
I
ω
et
ω
et
Commutation forcée Commutateur de courant
à diode d'isolement
L
Ic
MS
Tableau.1- Alimentation en courant des machines synchrones.

2
Alimentation Commande Description
Convertisseur de
tension
Onduleur
DCèAC
Onduleur à
commutation forcée
redresseur naturel ou
commandé
A
B
C
RedresseurOnduleurL
U Uid
Ic
MS
C
1+
1-
2+
2-
3+
3-
Réglage de la tension et de la
fréquence Commande 180°
réglage de l’amplitude
au niveau du
convertisseur d’entrée Vas
ω
et
180°
1+1-
2+2-3+3-2-
)
Commande 120°
réglage de l’amplitude
au niveau du
convertisseur d’entrée Vas
ω
et
120°
1+1-
2+2-3+3-2-3-
1+
60°
pour une charge ayant un
cosϕ ≈ 1. (
Modulation de
largeurs d’impulsions
Permet le réglage de la
tension, de la
fréquence et la
réduction du taux
d’harmoniques.
Ces modulations peuvent être
associées à une commande sur
120° ou 180°. Elles peuvent être
intersectives, précalculées ou
vectorielles.
Tableau 2 - Alimentation en tension des machines synchrones.
Le contrôle du couple est directement lié à celui des courants. Les alimentations
en tension (et donc les cycloconvertisseurs) peuvent être associées à des
régulations de courant effectuées par des comparateurs à hystérésis ou par des
régulateurs linéaires. Les interrupteurs sont commandés de manière à assurer les
courants désirés dans les phases de la machine.

3
Lors de l’utilisation d’un comparateur par hystérésis, la fréquence de
commutation est libre, elle est fixée par la charge. Ce mode de contrôle assure un
excellent suivi des consignes mais génère un large spectre de bruits et des pertes.
Le contrôle par régulateur linéaire et MLI est plus délicat. Mais l’utilisation des
techniques modernes de commande et l’amélioration des convertisseurs
(augmentation de la fréquence de travail) améliorent notablement ses
performances.
Comparateur à hystérésis Régulateur linéaire
+
-
Iaréf
Ia
+
-
Ibréf
Ib
+
-
Icréf
Ic
T1
+
T2
+
T3
+
T1
-
T2
-
T3
-
Etat
e
ec1
0
1 = T conducteur et T ouvert
0 = T conducteur et T ouvert
+-
+-
Etat
e
eb1
0
Etat
e
ea1
0
Etata
Etat
Etat
b
c
Etat :
+
-
Iaréf
Ia
+
-
Ibréf
Ib
+
-
Icréf
Ic
T1
+
T2
+
T3
+
T1
-
T2
-
T3
-
Iamodulante
Ibmodulante
modulante
Ic
Régulateur
Régulateur
Régulateur
Figure 11.8. - Régulateurs de courant.
Deux stratégies de commande sont envisageables :
à couple maximal,
à facteur de puissance unitaire.
Dans le cas d’une alimentation avec courant imposé (soit par commutateur de
courant soit par onduleur de tension avec contrôle du courant) et un flux à vide
donné (machine à aimants permanents ...), les variables de contrôle sont l’angle
Ψ entre Is et Vf , le courant et la pulsation statoriques.

4
Couple max
Dans le cas d’une machine à pôles lisses, il est obtenu pour Ψ = 0 . Mais dans ce
cas, la réaction d’induit interdit un fonctionnement à cosϕ = 1. Q est non nul.
Dans le cas de la machine à pôles saillants, le couple maximum disponible
augmente (pour un Is donné). Le fonctionnement à couple maximal est donné par
l’équation suivante [LEICHTER 80] :
( )
( )
ψψ ψ =− + −
−
arcsin f f ds qs s
ds qs s
L L I
L L I
222
8
4
Facteur de puissance unitaire
On désire cosϕ = 1 soit Q = 0. Dans ce cas Ψ= arcsin LI
s s
f
Ψ est non nul. La
machine ne fonctionne pas à couple maximal. On a :
( )
TpI LI
esfs s
f
= −3 1
2
2
ΨΨ
Dans le cas de la machine à pôles saillants, le fonctionnement à facteur de
puissance unitaire est obtenu pour [LEICHTER 80] :
( )
( )
ψψ ψ =− − −
−
arcsin f f ds qs qs s
ds qs s
L L L I
L L I
2 2
4
2
Si le rotor est bobiné, le flux Ψf peut être réglé par le courant d’excitation. Le
flux résultant est maintenu autour de la valeur nominale Ψn. Il est alors possible
de satisfaire aux deux objectifs :
(
)
cos ϕ=1
Te = 3p
Ψ
ns
I
On obtient des lois de commande [LAJOIE MAZENC 91B] du type Ψf (Is)et Ψ(Is)
prenant en compte l’échauffement de la machine du au passage dû courant
inducteur et à la non linéarité du circuit magnétique.
Dans le cas d’une machine alimentée en tension, les variables de contrôle sont
l’angle de décalage interne δ, la tension et la pulsation statorique. Mais la
démarche reste la même.

5
Machine synchrone autopilotée
Description du montage
1 2 3
1' 2'
3'
I
c
Commande
I
c
réf
-
+
MS
inducteur
R
S
T
Commande
Régulateur
Capteur
de position
1 2
La machine synchrone excitée de manière indépendante entraîne un capteur de
position qui permet
• la détection de la position relative rotor/stator c’est à dire la position du champ
inducteur par rapport au champ induit,
• la délivrance de signaux ont la fréquence est synchronisée sur la fréquence de
rotation de la machine.
Ces signaux sont mis en forme, amplifiés et isolés par l’intermédiaire de
transformateurs d’impulsions et envoyés sur les gâchettes des thyristors du
commutateur de courant 2 qui alimente l’induit de la machine synchrone. La
machine est « autopilotée ».
Ce convertisseur est lui-même alimenté par un second convertisseur 2 lui-même
alimenté par le réseau triphasé alternatif.
La liaison entre les deux commutateurs est réalisée par l’intermédiaire d’une
inductance L. Les deux convertisseurs fonctionnent en commutation naturelle.
L’extinction des thyristors du 1 est assurée par les tensions du secteur et celle
des thyristors du 2 est assurée par les tensions de la machine synchrone.
Le capteur de position
Il se compose
• d’une partie fixe solidaire du stator de la machine mais décalable
mécaniquement par rapport à celui-ci. Sur cette partie fixe sont fixés six étriers
dans lesquels sont placés les éléments excitateurs (diodes photo-émissives) et