Cours 6 - Interférences

Cours 6 - Interférences
v2015
Vocabulaire
Différence de marche : différence de distance parcourue , entre deux perturbations issues de
deux sources différentes arrivant en un même point .
Sources cohérentes : sources de perturbations émettant en phase (ou avec un déphasage
constant) des ondes (nécessairement de même fréquence , sinon il ne peut exister de relation de phase )
Interférences
Lorsque deux ondes se superposent en un même
point il y aura addition des deux perturbations.
Si les sources de ces ondes sont cohérentes on
discernera à l'oeil un motif permanent
« d’interférences » .
(gauche : interf. d’ondes méca / droite interf.
d’oem – « franges » )
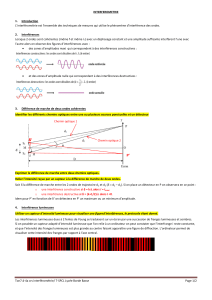
Interférences constructives et destructives
Les deux graphes ci-dessous représentent les perturbations subies par un point de l’espace, au cours du temps.
 (gauche) Si deux perturbations issues de sources cohérentes arrivent en phase en un même point de l'espace, l'amplitude de
l'onde résultante sera maximale . L’interférence est « constructive » . ( TP / Donald est secoué un max)
 (droite) Si par contre elles arrivent en opposition de phase , l'amplitude de l'onde résultante sera minimale . L’interférence est
destructive . ( TP : Coin-Coin ne sent rien)
… (hypothèse : sources des perturbations en phase)
Condition sur la
différence de marche
(diff. de longueur de trajet)
Condition sur le retard
( différence de duréede trajet )
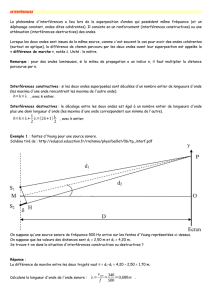
Interférences à deux ondes
constructives
 = n 
t = n T
Interférences à deux ondes
destructives
 = n  + /2
t = n T + T/2

Interférences en lumière monochromatique
dispositif de Young
 le dispositif de Young utilise la diffraction
pour générer deux sources cohérentes S1
et S2 à partir de S , et les faire interférer
entre elles.
 Aux endroits satisfaisant aux conditions
d’interférences destructives, ( deux
ondes lumineuses en opposition de
phase) on voit des « franges sombres »
 Ailleurs, l’addition des ondes donne une
perturbation périodique non nulle
dépendant du temps. Mais l'oeil n'est pas
capable de « suivre » ses variations
(domaine visible : fréquences de l’ordre de 5 1016 Hz) . Il verra simplement de la lumière.
 Dans le cas du dispositif de Young, on montre que l'interfrange (distance entre deux franges brillantes successives, ou deux
franges sombres successives) est tel que i =  D/a ( longueur d'ondes distance fentes/écran a distance entre fentes )
Interférences en lumière blanche
Il ne peut y avoir d’interférences qu’entre ondes de même fréquence .
Dans le cas d’une lumière polychromatique, le motif d’interférences sera donc la superposition de tous les motifs d’interférenecs
polychromatiques. (voir manuel par3.1 p97)
Couleurs interférentielles
 Lorsque de la lumière blanche arrive sur une
couche de matériau très mince (bulle de savon, film
d'essence sur de l'eau , dépôt métallique sur du
verre etc...) , il existe une possibilité d'interférences
entre les ondes réfléchies par la face avant et celles
réfléchies par la face arrière .
 Pour une différence de marche donnée (dépendant
de l'épaisseur de la couche mince , de l’indice
optique n , et des angles en jeu) il y aura
interférences constructives pour certaines l.
d’ondes et destructives pour d’autres.
 La lumière blanche « perdant » certaines couleurs,
elle deviendra colorée. ( synthèse soustractive ) .
 En pratique, ceci n'arrive que pour des couches présentant une épaisseur du même ordre de grandeur que les longueurs
d'ondes concernées.
(rappel de seconde : indice de réfraction d'un milieu (indice optique)
n (air) = 1 n(eau) = 1,33
L'indice n intervient dans certains calculs de différence de marche, lorsque les ondes qui
interfèrent passent par des milieux différents (comme cas précédent) .
La durée que met la lumière pour traverser une longueur L dans un matériau d’indice n est t = L / v or v = c / n d’où t = nL / c .
Un trajet L dans un milieu d’indice n est donc équivalent à un trajet dans le vide de longueur n L )
Dualité onde-corpuscule et interférences Lire page 406 du manuel
Lorsque l’on reprend le dispositif des fentes d’Young et que l’on envoie un par un
des photons sur les fentes , on voit apparaître …. des franges d’interférences !!!
On s’attendrait à ce que les photons franchissent simplement les fentes comme
des billes…
Ceci est (avec la diffraction des électrons) une autre illustration frappante de la
dualité onde-corpuscule.
On interprète le phénomène ainsi : la position d’un photon ne pouvant être
connue avec précision, celui-ci est décrit au niveau des fentes comme une
« onde de probabilité de présence » . On se ramène alors à une situation
« classique » d’interférences . Par contre le photon devient « réel » au moment
de sa détection sur l’écran.
Détail amusant, si l’on essaie de savoir par un moyen quelconque quelle fente le
photon passe, l’expérience ne marche pas !
Exos recommandés : chap 6 : 2, 4, 18, 24, 29 chap 20 : act 3