Trigonométrie classe de troisième.

2012
Trigonométrie classe de troisième.
I-
Introduction.
C
L’hypoténuse
Côté opposé à l’angle
A
B
A
Côté adjacent à
l’angle A
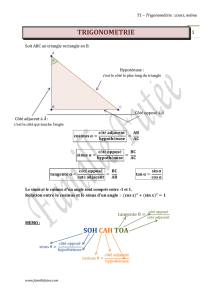
II- Cosinus, sinus, tangents.
Définition :
Dans un triangle rectangle :

Le cosinus d’un angle aigu est égal au rapport :
𝑳𝒂 𝒍𝒐𝒏𝒈𝒖𝒆𝒖𝒓 𝒅𝒖 𝒄ô𝒕é 𝒂𝒅𝒋𝒂𝒄𝒆𝒏𝒕 à 𝒄𝒆𝒕 𝒂𝒏𝒈𝒍𝒆
𝑳𝒂 𝒍𝒐𝒏𝒈𝒖𝒆𝒖𝒓 𝒅𝒆 𝒍′ 𝒉𝒚𝒑𝒐𝒕é𝒏𝒖𝒔𝒆

Le sinus d’un angle aigu est égal au rapport :
𝑳𝒂 𝒍𝒐𝒏𝒈𝒖𝒆𝒖𝒓 𝒅𝒖 𝒄ô𝒕é 𝒐𝒑𝒑𝒐𝒔é à 𝒄𝒆𝒕 𝒂𝒏𝒈𝒍𝒆
𝑳𝒂 𝒍𝒐𝒏𝒈𝒖𝒆𝒖𝒓 𝒅𝒆 𝒍′ 𝒉𝒚𝒑𝒐𝒕𝒆𝒏𝒖𝒔𝒆

La tangente d’un angle aigu est égale au rapport :
𝑳𝒂 𝒍𝒐𝒏𝒈𝒖𝒆𝒖𝒓 𝒅𝒖 𝒄ô𝒕é 𝒐𝒑𝒑𝒐𝒔é à 𝒄𝒆𝒕 𝒂𝒏𝒈𝒍𝒆
𝑳𝒂 𝒍𝒐𝒏𝒈𝒖𝒆𝒖𝒓 𝒅𝒖 𝒄ô𝒕é 𝒂𝒅𝒋𝒂𝒄𝒆𝒏𝒕 à 𝒄𝒆𝒕 𝒂𝒏𝒈𝒍𝒆
cos(𝐴̂) =
𝐴𝐵
𝐴𝐶
Les mathématiques au collège
sin(𝐴̂) =
𝐵𝐶
𝐴𝐶
tan(𝐴̂) =
𝐵𝐶
𝐴𝐵
Page 1
2012
Trigonométrie classe de troisième.
Remarque :
𝑐𝑜𝑠 2 (𝐴̂) + 𝑠𝑖𝑛2 (𝐴̂) = (
𝐴𝐵 2
𝐵𝐶 2
) +( )
𝐴𝐶
𝐴𝐶
=
𝐴𝐵2 𝐵𝐶 2
+
𝐴𝐶 2 𝐴𝐶 2
=
𝐴𝐵2 + 𝐵𝐶 2
𝐴𝐶 2
D’après le théorème de Pythagore : 𝐴𝐵2 + 𝐵𝐶 2 = 𝐴𝐶 2 donc
𝐵𝐶
tan(𝐴̂) =
=
𝐴𝐵
2
𝐴𝐶
𝑐𝑜𝑠 2 (𝐴̂) + 𝑠𝑖𝑛2 (𝐴̂) = 𝐴𝐶 2 = 1
𝐵𝐶
𝐴𝐶 = 𝑠𝑖𝑛(𝐴̂)
𝐴𝐵
𝑐𝑜𝑠(𝐴̂)
𝐴𝐶
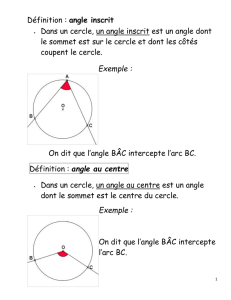
III- Angle inscrit, angle au centre.
Définitions :
On appelle angle inscrit, un angle dont le sommet est sur un cercle, et les deux côtés
coupent le cercle en deux points.
On appelle angle au centre un angle dont le sommet est le centre d’un cercle et les deux
côtés coupent le cercle en deux points.
Propriétés :
1) Angle au centre et angle inscrit, interceptent le même arc.
̂ ) et l’angle au centre (𝐵𝑂𝐶
̂ ) interceptent le même arc 𝐴𝐵
̂ du cercle.
Si l’angle inscrit (𝐵𝐴𝐶
̂ = 𝟐 × (𝑩𝑨𝑪)
̂
(Voir la figure ci-dessus). Alors (𝑩𝑶𝑪)
Les mathématiques au collège
Page 2
Trigonométrie classe de troisième.
2012
2) Deux angles inscrits qui interceptent le même arc.
̂ 𝑒𝑡 𝐵𝐴𝐶
̂ 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡𝑒𝑛𝑡
𝐿𝑒𝑠 𝑎𝑛𝑔𝑙𝑒𝑠 𝐵𝐷𝐶
̂ 𝑑𝑜𝑛𝑐 𝑖𝑙𝑠 𝑠𝑜𝑛𝑡 é𝑔𝑎𝑢𝑥.
𝑙𝑒 𝑚ê𝑚𝑒 𝑎𝑟𝑐 𝐵𝐶
̂ = 𝑩𝑨𝑪
̂
𝑩𝑫𝑪
Les mathématiques au collège
Page 3