Les mesures de dispersion

CHAPITRE 8
Les mesures de dispersion
Les mesures de dispersion améliorent la description des séries sta-
tistiques en quantifiant l’étalement, la variabilité et l’homogénéité des
données. Toutefois, les mesures de dispersion ne se calculent que pour
les variables quantitatives.
1. L’étendue
1.1. Introduction à l’étendue. L’étendue, symbolisée par E, ca-
ractérise l’étalement d’une série par l’écart entre la valeur maximale et
la valeur minimale d’une série
E=Vmax −Vmin
1.2. Étendue pour des variables groupées par valeurs. Afin
de calculer l’étendue pour une variable quantitative discrète, il suffit
de soustraire la plus grande valeur à la plus petite valeur.
Exemple 8.1.Trouvons l’étendue.
Tab. 1. Répartition des répondants, selon le niveau d’aptitude à la lecture.
Niveau Nombre de répondants Cumulatif des répondants
1 17 17
2 23 40
3 55 95
4 155 250
Total 250
E=Vmax −Vmin
= 4 −1
= 3 niveaux
35

36 8. LES MESURES DE DISPERSION
1.3. Étendue pour des variables groupées par classe. Afin
de calculer l’étendue pour une variable quantitative continue, il suffit
de soustraire la borne supérieure de la classe supérieure à la borne
inférieur de la classe inférieur.
Exemple 8.2.Trouvons l’étendue.
Tab. 2. Répartition des monarques d’Angleterre (roi ou
reine) selon la durée de leur règne, 827-1952.
Durée du règne Nombre de monarques Fréquences cumulées
0-10 22 22
10-20 16 38
20-30 11 49
30-40 7 56
40-50 1 57
50-60 3 60
Total 60
Source : R. Porkess, Dictionary of Statistics, Londres, Collins, 1988, p.70.
E=Limsup −Liminf
= 60 −0
= 60 ans
2. L’écart-type et la variance
La description de l’étalement d’une distribution peut être affinée.
Pour ce faire, on utilise la variance et l’écart-type qui tiennent compte
de l’ensemble des données. Plus l’écart-type est faible, plus les données
sont dispersées autour de la moyenne. Inversement, plus l’écart-type
est élévée, plus les données sont dispersées loin de la moyenne.
2.1. Le calcul de l’écart-type pour des variables groupées
par valeurs. L’écart-type d’une population de taille N est symbolisée
par
σ=
N
i=1
(xi−µ)2
N
L’écart-type d’un échantillon de taille nest symbolisée par
s=
k
i=1
(xi−¯x)2fi
n−1

2. L’ÉCART-TYPE ET LA VARIANCE 37
L’écart-type est la racine carrée de la moyenne des écarts entre les
valeurs et la moyenne.
2.2. Le calcul de l’écart-type pour des variables groupées
par classes. L’écart-type d’un échantillon de taille ngroupées en
classe est symbolisée par
s=
k
i=1
(mi−¯x)2fi
n−1
L’écart-type est la racine carrée de la moyenne des écarts entre les
milieux des classes et la moyenne.
Exemple 8.3.Trouvons l’écart-type.
Tab. 3. Répartition des répondants, selon le niveau d’aptitude à la lecture.
Niveau Nombre de répondants Cumulatif des répondants
1 17 17
2 23 40
3 55 95
4 155 250
Total 250
Supposons que nous savons que la moyenne est 3,39 .
s=
k
i=1
(xi−¯x)2fi
n−1
=(1 −3,39)2×17 + (2 −3,39)2×23 + (3 −3,39)2×55 + (4 −3,39)2×155
249
= 0,91 niveau
Exemple 8.4.Trouvons l’étendue.
Supposons que nous savons que la moyenne est 18.
s=
k
i=1
(mi−¯x)2fi
n−1
=(5 −18)2×22 + (15 −18)2×16 + ... + (55 −18)2×3
249
= 13,81 ans

38 8. LES MESURES DE DISPERSION
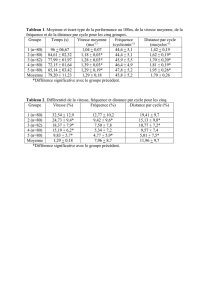
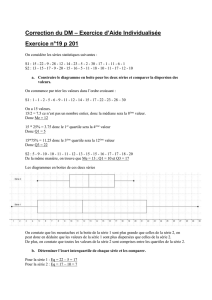
Tab. 4. Répartition des monarques d’Angleterre (roi ou
reine) selon la durée de leur règne, 827-1952.
Durée du règne Nombre de monarques Fréquences cumulées
0-10 22 22
10-20 16 38
20-30 11 49
30-40 7 56
40-50 1 57
50-60 3 60
Total 60
Source : R. Porkess, Dictionary of Statistics, Londres, Collins, 1988, p.70.
Il est souvent très long de faire le calcul de l’écart-type à la main. Il
est préférable d’utiliser sa calculatrice. Vous pouvez consulter le guide
de la calculatrice sur le site Internet.
2.3. La variance. La variance est le carré de l’écart-type. L’in-
convénient de la variance est qu’elle n’est pas exprimée dans l’unité de
la variable.
3. Le coefficient de variation
Le coefficient de variation permet de comparer la variabilité de deux
séries qui ont des moyennes très différentes ou même qui ne sont pas
exprimées dans les mêmes unités puisque le coefficient de variation
exprime l’écart-type en pourcentage de la moyenne.
CV =s
¯x×100%
Le coefficient de variation donne l’homogénéité de la série, si le coeffi-
cient de variation est inférieur à 15%, on considère que les données sont
homogènes et inversement, si le coefficient de variation est supérieur à
15%, on dit que les données sont hétérogènes.