Q - GSEM Committee

Notes de cours d’étudiants
Selon l’intitulé :
« ECONOMIE DE LA CONCURRENCE»
Prof. D. KYLYMNYUK
Notes originales fournies par :
NOM
PRENOM
ANNEE
JEAN-MAIRET
MICHAEL
2011-2012
Dernière mise à jours par :
NOM
PRENOM
ANNEE
Avertissements : Le présent document regroupe des notes d’étudiants relatives au cours nommé ci-
dessus. Il est mis gratuitement à disposition des étudiants par le CHEC ; son contenu ne peut en aucun
cas être vendu.
De plus, ce document n’est pas un polycopié officiel : son contenu n’est pas garanti, il ne dispense donc
pas d’être présent aux cours.
Enfin, quiconque bénéficie du présent support se doit de le mettre à jours en corrigeant les éventuelles
erreurs et en le complétant (merci de renvoyer les documents modifiés à l’adresse [e-mail])

CPP :
Max π(Q) = PQ – C(Q)=
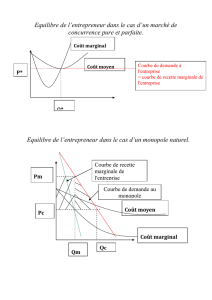
Q* est satisfait quand π'(Q*) = P – C'(Q*) = 0
Le seuil de rentabilité, pour qu'une entreprise entre sur le marché il faut que
sont profit maximum qu'elle peut espérer réaliser soit positif :
π(Q*) = PQ* - C(Q*) = Q*[P –
C(Q*)/Q*] π(Q*) > 0 P > CM(Q*)
Monopole :
Les monopoles possèdes tous un pouvoir de marché ce qui leurs permettent
d'influencer les prix.
Les monopole se crée lorsqu'il y a des barrières à l'entrée :
• Contrôle d'une ressources naturelles essentielle
• Barrière légale (brevets)
• Economies d'échelles (monopole naturel)
Revenu totale : (la quantité influence le prix)
R(Q) = P (Q)⋅Q Pour vendre augmenter le volume des ventes (Q) il faut
diminuer le prix [P(Q)]
Revenu marginal :
Rm(Q) = P (Q)+Q⋅P ' (Q)
Effet direct positif
Effet indirect négatif
Rm,RM,P
D
Recette moyenne :
a/b
Q
= a – bp
RM (Q)= RT (Q)= P (Q)⋅Q =P (Q)
Q
Q
Recette marginal :
-2/b
Rm(Q)=
∂ RT (Q)
=
∂ [ P(Q)⋅Q]
-1/b
RM
∂ Q
∂Q
Rm
a/2
a
Q
Revenu marginal et élasticité :
Rm(Q) = P(Q) + QP'(Q) = P(Q)
[1+P ' (Q)
PQ(Q)
]

Rm(Q) = P(Q)[1 + ƞP] = P(Q) [1+1ƞ ]
• Demande élastique quand ƞ < -1 Rm(Q) > 0, P(Q) croissant.
• Demande élastique unitaire, ƞ = -1 Rm(Q) = 0 R(Q) constant.
• Demande inélastique, ƞ > -1 Rm(Q) < 0 P(Q) décroissant.
Un monopole ne va jamais produire dans la section inélastique de la demande.
Maximisation du profit :
max π(Q) = QP(Q) – C(Q)
π'(Q*) = P(Q*) + Q*P'(Q*) - C'(Q*) =
0 Rm(Q*) = Cm(Q*)
π''(Q) < 0 ∂ Rm(Q)< ∂ Cm(Q)
∂ Q ∂ Q
P(Q) [1+ 1ƞ ]=Cm(Q)
P (Q)= 1 Cm(Q)>Cm(Q)
1+ 1ƞ

Prix-Plafond :
L'état pour augmenté la quantité produite par un monopole peut fixer un prix
plafond, de ce fait si il ne peut plus augmenter ces prix il a intérêt à vendre le
plus possible. Le problème c'est qu'il est difficile de connaître le prix à fixer, si le
prix est trop faible cela pourrait conduire le monopole à quitter le marché.
Imposition et subvention du monopole :
Si des taxes doivent être payé cela augmente les Cm ce qui diminue
encore la quantité. Donc pour augmenter les quantités il faudrait
subventionner le monopole mais qui va payer ces taxes.
Imposition sur la profit :
max(1-T)π(Q) = (1-T)[P(Q)Q – C(Q)]
Monopole naturel :
CF élevée et CV relativement faible, ce qui implique rendement croissant : CM décroissant
Monopole avec des rendements croissants :
P,Rm,
CM,Cm
P*
CM
Cm
P(Q)
Q*
Q
Rm(Q)
Lorsqu'un monopole a un rendement
décroissant il ne va pas produire jusqu'à
l'infini car lorsque la courbe de CM coupe
celle de P(Q) le profit devient négatif.
Taille minimum efficiente (TME)
Cela signifie qu'un monopole va commencer à faire du profit qu'a partir d'une
certaine quantité produite. Sur un marché de petite taille parfois il vaut mieux
quîl y ait une seul entreprise car le demande n'est pas assez élevée pour
que deux entreprises puissent produire assez pour être efficiente.
Réglementation du monopole naturel : (I)
Il faudrait fixer un prix qui est égale au Cm mais dans ce cas le profit
serait négatif car CM>Cm=P. Il faudrait subventionner le monopole pour
qu'il reste sur le marché.
Subvention que doit
verser l'état au monopole.
Qr

Réglementation du monopole naturel : (II)
Si l'état impose la tarification au CM le profit étant nul
il n'y a pas besoin de subvention. Mais par contre la
quantité produite sera plus faible qui si l'état
subventionnait la différence entre le Cm et le CM.
Monopole discriminant :
Un bien qui est homogène est vendu à des prix différent à différentes
classe de la population. On en distingue trois types :
1. Premier degré : chaque acheteur achète le produit à son prix de réserve
donc prix différent pour chaque consommateur.
2. Second degré : La tarification est différentes en fonction des quantités acheté.
3. Troisième degré : Le prix est différent en fonction du groupe de consommateurs.
Discrimination du troisième degré le modèle :
Prenons deux groupes P1(Q1) et P2(Q2) leur fonction de demande est différentes,
mais la fonction de coût pour l'entreprise est identique. Dans ce cas le monopole
choisit les quantités (et par conséquent le prix) chacun des groupes de manières à
maximiser le profit. Ce qui au final revient à égaliser le Rm de chaque groupe.
Max π = P1(Q1)Q1 + P2(Q2)Q2 – C(Q1 + Q2)
Rm(Q1)=P1 (1+ 1 )=Cm(Q1+Q2)
ƞ1
Rm(Q2)=P2 (1+ 1 )=Cm (Q1+Q2)
ƞ2
P1 (1+ ƞ1 )=P2 (1+ ƞ1 )
1
2
1+ 1
P
1
=
ƞ
2
P2
1+ 1
ƞ1
P1>P2 ⇔ ƞ1>ƞ2
Les prix vont varié en fonction de
l'élasticité de la demande de
chaque groupe. Celui qui en valeur
absolu a l'élasticité la plus élevé
payera le prix le moins élevé.