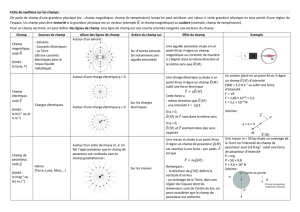
EXEMPLES DE CHAMPS 1 Champ magnétique

1
ère
S Comprendre 9 : Exemples de champs page 1/5
E XEMPLES DE C HAMPS
1 Champ magnétique
1.1 Détection
Une aiguille aimantée permet de mettre en évidence l’existence d’un champ magnétique en
un point de l’espace
Remarque :
On lui donne parfois le nom d’objet-test pour les champs magnétiques.
L’orientation (direction et sens) prise par l’aiguille aimantée dépend du point où elle est située, le champ
magnétique détecté a donc des propriétés vectorielles.
Le champ magnétique est un champ vectoriel
1.2 Le vecteur champ magnétique
Le champ magnétique en un point M quelconque de l’espace est caractérisé par le vecteur
champ magnétique dont les caractéristiques sont les suivantes :
• sa direction est donnée par l'orientation d'une aiguille aimantée placée en M
• son sens va du pôle sud vers le pôle nord de cette aiguille aimantée
• sa valeur (ou intensité) se mesure avec un teslamètre et se note B(M) exprimé en tesla
(T)
Le point origine du vecteur champ magnétique est le point M considéré
1.3 Spectres magnétiques
Une ligne de champ magnétique est une courbe tangente en chacun de ses points au vecteur
champ magnétique . Elle est orientée dans le même sens que le vecteur
Les lignes de champ se referment sur elles-mêmes, elles sortent de l’aimant par le pôle
nord et y entrent par le pôle sud
L’ensemble des lignes de champ d’un aimant forme son spectre magnétique
Remarques :
La ligne de champ est tangente au vecteur , donc le vecteur champ magnétique est tangent, en chaque point, à la
ligne de champ.
Dans l’entrefer d’un aimant en U, les lignes de champ sont parallèles entre elles (et également espacées), le
champ magnétique y est donc uniforme.
1.4 Le champ magnétique terrestre
L’aiguille de la boussole se dirige vers le Nord géographique car elle est sensible au champ magnétique créé par
la Terre. Comme beaucoup de corps célestes (étoile, planète…) la Terre est une source de champ magnétique.
La Terre crée dans son voisinage un champ magnétique appelé champ magnétique terrestre
ou champ géomagnétique.
Remarques :
La direction donnée par l’aiguille aimantée ne correspond pas exactement à la position du nord
géographique. L’écart angulaire entre les deux est appelé déclinaison magnétique.
Selon les latitudes, le champ magnétique terrestre est plus ou moins incliné par rapport à l’horizontale,
on parle d’inclinaison magnétique
La valeur de la composante horizontale du champ magnétique terrestre, notée B
H
, est d’environ 2,0×10
-2
mT ou 2,0×10
-5
T

1
ère
S Comprendre 9 : Exemples de champs page 2/5
2 Le champ électrostatique
2.1 Détection
Un pendule électrostatique chargé permet de mettre en évidence l’existence d’un champ
électrostatique en un point de l’espace.
Remarque :
On lui donne parfois le nom d’objet-test pour les champs électrostatiques.
Le champ électrostatique est un champ vectoriel
2.2 Le vecteur champ électrostatique
Le champ électrostatique en un point M de l’espace et la force électrostatique qui
s’exerce sur un corps portant la charge q et placé en ce point M vérifient :
=
• la direction de est la même que celle de
• et sont de même sens si la charge q est positive (de sens opposé si q est négative)
• la valeur du champ électrique vérifie : E =
q en C F en N E en N.C
-1
Le point origine du vecteur champ électrostatique est le point M considéré
2.3 Spectres électrostatiques
Une ligne de champ électrostatique est une courbe tangente en chacun de ses points au
vecteur champ électrostatique .
Elle est orientée dans le même sens que le vecteur
Remarque :
La ligne de champ est tangente au vecteur , donc le vecteur champ électrostatique est tangent, en chaque point, à
la ligne de champ.
2.4 Cas du condensateur plan
Un condensateur plan est formé de deux plaques métalliques parallèles séparées par un
isolant.
Le champ électrostatique à l’intérieur d’un condensateur plan est uniforme :
• sa direction est perpendiculaire aux plaques
• son sens va de la plaque positive vers la plaque négative
• sa valeur dépend de la tension U entre les plaques et de la distance d entre celles-
ci :
E =
U en V d en m E en V.m
-1
Remarque :
Les unités V.m
-1
et N.C
-1
sont équivalentes mais
pour E on préfère utiliser le V.m
-1
.

1
ère
S Comprendre 9 : Exemples de champs page 3/5
3 Champs de pesanteur
3.1 Détection
Un objet de masse m permet de mettre en évidence le champ de pesanteur
Remarque :
On lui donne parfois le nom d’objet-test pour le champ de pesanteur.
L’orientation prise par l’objet dépend de la latitude, le champ de pesanteur a donc des propriétés vectorielles.
Le champ de pesanteur est un champ vectoriel
3.2 Champ de pesanteur
Au voisinage de la Terre, l’objet est soumis à son poids , ce résultat peut être interprété en termes de champ
Le champ de pesanteur en un point M de l’espace et le poids d’un objet de masse m
placé en ce point M vérifient :
=
• la direction de est la même que celle de (verticale du lieu)
• et sont de même sens (vers le bas)
• la valeur du champ de pesanteur vérifie : g =
m en kg P en N g en N.kg
-1
Le point origine du vecteur champ de pesanteur est le point M considéré.
Remarque :
Dans une zone de l’espace réduite (quelques km) on parle de champ de pesanteur local.
Le champ de pesanteur local est un considéré comme un champ uniforme.
3.3 Champ de gravitation
Tous les corps qui possèdent une masse exercent les uns sur les autres des forces d’interaction gravitationnelles
attractives qui peuvent être interprétées en termes de champ
Le champ de gravitation qui existe autour d’un objet massique est un champ vectoriel.
Il est centripète : toutes les lignes de champ sont orientées vers le centre de l’objet
massique à l’origine du champ
Le champ de gravitation G en un point M de l’espace et la force d’interaction
gravitationnelle s’exerçant sur un objet de masse m placé en ce point M vérifient :
G =
Remarque :
La direction du vecteur champ de gravitation est la droite joignant le point M au centre de l’objet à l’origine du
champ.
Le sens du vecteur champ de gravitation va du point M vers l’objet à l’origine du champ
La valeur du champ de gravitation est G = Comme : F = G×M×m/d², alors G =
3.4 Champs de gravitation et de pesanteur
En raison du mouvement de rotation de la Terre, le poids d’un objet n’est pas rigoureusement identique à
l’interaction gravitationnelle entre la Terre et cet objet, par conséquent les champs de pesanteur et de gravitation ne
sont pas rigoureusement identiques. Cela la différence entre les deux est faible et on pourra admettre qu’ils sont
équivalents.
Au voisinage de la Terre : = G
Terre