Expérience de Rutherford - Physique PCSI1 Lycée Michelet

PCSI1Lycée Michelet
Expérience de Rutherford
On s’intéresse ici à une expérience historique réalisée par H.Geiger et
E.Marsden sous la direction de E.Rutherford. Les résultats de cette expé-
rience, publiés en 1909 1ont permis une avancée décisive dans notre com-
préhension de la structure des atomes. À l’époque les résultats semblent si
surprenants que Rutherford mettra deux ans avant de publier un nouveau
modèle atomique. À ce titre, Ernest Rutherford est considéré comme le
fondateur de la physique nucléaire.
Antérieurement à cette expérience, la matière était conçue sous la forme
d’atomes électriquement neutres, contenant deux parties chargées électri-
quement de façons opposées, la partie chargée négativement pouvant être
arrachée à l’atome (rayons cathodiques).
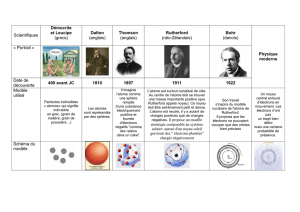
L’atome était représenté comme
un «pudding aux raisins» plum
pudding : une «pâte» positive
avec des inclusions négatives
(modèle de J.J. Thomson).
En 1908, Rutherford a déjà obtenu un prix Nobel pour ses travaux sur
la radioactivité. Il a montré entre autres, que les rayonnements αproduits
lors de désintégrations radioactives correspondaient à des noyaux d’hélium.
Il va utiliser ces particules αpour sonder la matière. Pour cela, il bombarde
des cibles constituées de feuilles de métal (par exemple de l’or) et observe
les particules transmises. La surprise vient du fait qu’une petite partie
des particules αest rétrodiffusée, et repartent en direction de la source.
Ces événements sont incompatibles avec le modèle de l’époque (modèle de
J.J.Thomson).
1. H.Geiger, E. Marsden. On a Diffuse Reflection of the α-Particules. Proceedings of
the Royal Society (1909) : 495-500.
Schéma de l’expérience
Rutherford dira :"C’est l’événement le plus incroyable qui me soit jamais
arrivé. C’est à peu près aussi incroyable que de tirer un obus de 15 pouces
sur une feuille de papier et qu’il rebondisse et vous touche."
1

PCSI1Lycée Michelet
Analyse : mise en équation
Une particule α(correspondant à un noyau d’hélium) de masse met
de charge q= 2e, venant de l’infini avec la vitesse −→ vo, s’approche avec un
paramètre d’impact b=OH d’une cible (noyau d’or) de masse Mm
et de charge Ze (pour l’or Z= 79). On se place dans le référentiel du
laboratoire, dans lequel on supposera le noyau d’or fixe.
1) On note ~σ0, le moment cinétique en O, dans le référentiel du labora-
toire, de la particule α.
1.a ) Justifier que ce moment cinétique est une constante vectorielle
du mouvement.
1.b) Exprimer ~σ0, en fonction de m,b,v0et d’un des vecteurs unitaires
du trièdre direct (~ex, ~ey, ~ez). On calculera pour cela ~σ0en M0correspondant
à la position initiale de la particule α, infiniment éloignée de O.
2) Établir l’expression de ~σ0en fonction de m,r,˙ θet d’un des vecteurs
unitaires du trièdre direct (~ex, ~ey, ~ez).
3) Déduire des deux questions précédentes une relation entre b,v0,ret
˙
θ. Compte-tenu de l’orientation choisie, quel est le signe de ˙ θ?
4) Montrer que −→ v∞−−→ vo=k
m v0b(−→
eθ∞−−→ eθ0), où k=2Ze2
4πε0
et où
l’indice 0concerne les grandeurs au départ et l’indice ∞les grandeurs quand
la particule est de nouveau infiniment éloignée du noyau. (Indication : on
utilisera la relation établie au 3) pour mettre le principe fondamental de la
dynamique sous une forme facilement intégrable).
5) En déduire la déviation Dde la particule. On exprimera tan D
2en
fonction de k,m,bet v0. Pour établir cette relation, il suffit de projeter la
relation du 4) soit sur ~uxsoit sur ~uy.
6) On note rmin la distance minimale de plus courte approche du noyau
(rmin =OS).
6.a) En utilisant la conservation du moment cinétique, établir une re-
lation entre b,rmin =OS,v0et vmin =vSla norme vitesse au point S.
6.b) En exploitant de plus la conservation de l’énergie mécanique, dé-
terminer la distance minimale rmin de plus courte approche du noyau en
fonction de k,Ec0énergie cinétique des particules incidentes (Ec0=1
2mv2
0)
et b, puis en fonction de k,Ec0et D.
6.c) Les particules αutilisées par Rutherford avaient une énergie ci-
nétique de 7,7MeV. Calculer la valeur de rmin associée à une déviation
D= 150◦(on rappelle que 1eV= 1,6.10−19 J). Qu’a-t-on pu conclure à
l’époque sur les dimensions du noyau atomique ?
6.d) Dans quelle direction sont déviées les particules αqui se seront le
plus approchées du noyau. Retrouver directement la valeur de rmin dans ce
cas et faire l’application numérique.
6.e) Justifier, avec les connaissances actuelles, que seule l’interaction
électromagnétique est à considérer pour interpréter cette expérience.
Données :
ε0= 8,85.10−12 F.m−1
e= 1,60.10−19 C
2

PCSI1Lycée Michelet
Conclusion
Rutherford dira : "À moins que l’on ne suppose que les atomes aient
un noyau chargé de petites dimensions, il est impossible d’expliquer les
faits expérimentaux de la diffusion des particules α..." L’idée d’un noyau
atomique était née.
Vers un traitement quantique de l’atome
Un peu plus tard, Niels Bohr, qui sera étudiant de Rutherford, s’inter-
rogera sur la stabilité de ce modèle. Il écrira en 1913 : "Pour expliquer
les résultats des expériences sur la diffusion des rayons αpar la matière,
le Professeur Rutherford a fourni une théorie de la structure des atomes.
D’après cette théorie, les atomes sont constitués d’un noyau chargé
positivement entouré d’un système d’électrons maintenus ensemble par des
forces attractives du noyau : la charge négative totale des électrons est égale
à la charge positive du noyau. De plus on suppose que le noyau est le siège
de la principale partie de la masse de l’atome et qu’il a des dimensions
extrêmement petites en comparaison de celle de la totalité de l’atome [...]
Cependant dans une tentative d’explication de la matière sur
la base de ce modèle d’atome, nous rencontrons de sérieuses
difficultés provenant de l’apparente instabilité du système d’élec-
trons [...] Le résultat de la discussion de ces questions semble
être une reconnaissance générale de l’insuffisance de l’électrody-
namique classique à décrire le comportement d’un système de
dimension atomique. Quelle que puisse être la modification des
lois du mouvement des électrons, il semble qu’il soit nécessaire
d’introduire dans les lois en question une quantité étrangère à
l’électrodynamique : la constante de Planck ou, comme elle a été
souvent appelée, le quantum élémentaire d’action. "
La mécanique quantique, qui verra le jour plus une bonne décennie plus
tard, permettra de résoudre le problème de stabilité de l’atome.
3