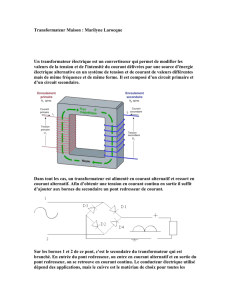
Transformateurs monophasés Correction des exercices III, IV et V

Transformateurs monophasés
Correction des exercices III, IV et V
Exercice III
Les essais suivants ont été réalisés sur un
transformateur monophasé dont le schéma équivalent
est représenté ci-contre.
•Essai à vide : valeurs efficaces des tensions
primaire et secondaire : 230 V et 85 V ; intensité
efficace du courant primaire : 0,7 A et puissance
active au primaire 40 W.
•Essai en court-circuit : valeur efficace du courant primaire : 8 A ; la valeur efficace de la tension primaire
est égale à 25 V et la puissance active au primaire est égale à 67 W.
3. Exploitation de l'essai à vide
c. Calculer le rapport de transformation
m=V20
V1
=85
230 =0,37
d. Calculer la puissance réactive lors de cet essai.
Les puissances apparente
S0
, active
P0
et réactive
Q0
sont reliées par
S0
2=P0 2+Q0 2
avec
S0=V1.I10=230×0,7=161 VA
Ce qui donne
Q0=
√
S0
2– P0 2=
√
1612–402=156 var
e. Calculer Rf et Lm.
La résistance
Rf
« consomme » la puissance active
P0
ce qui permet d'écrire
P10=V1
2
Rf
et donc
Rf=V1
2
P10
=2302
40 =1320 Ω
L'inductance
Lm
« consomme » la puissance réactive
Q0
ce qui permet d'écrire
Q10=V1
2
Lmω
et
donc
Lm=V1
2
Q10 ω=2302 156×2π50 =1,08 H
(remarque :
ω=2pi f
et f = 50 Hz)
4. Exploitation de l'essai en court-circuit
Pour cet essai, le transformateur est supposé parfait pour les intensités (ce qui signifie que les influences de
Rf et Lm sont négligées).
c. Calculer l'intensité efficace du courant secondaire pour cet essai.
On utilise la relation pour les courants du transformateur parfait :
I2cc=1
mI1cc
soit
I2cc=1
0,37 8=21,6 A
d. Calculer la puissance réactive pour cet essai.
Les puissances apparente
Scc
, active
Pcc
et réactive
Qcc
sont reliées par
Scc
2=Pcc 2+Qcc 2
avec
Scc=V1cc .I1cc=25×8=200 VA
Ce qui donne
Qcc=
√
Scc
2– Pcc 2=
√
2002–672=188 var
Transformateurs monophasés Page 1 TS1 ET 2013-2014

e. Calculer Rs et Xs.
La résistance
Rs
« consomme » la puissance active
Pcc
ce qui permet d'écrire
Pcc=RsI2cc
2
et donc
Rs=Pcc
I2cc
2=67
21,62=0,143 Ω
La réactance
Xs
« consomme » la puissance réactive
Qcc
ce qui permet d'écrire
Qcc=XsI2cc
2
et
donc
Xs=Qcc
I2cc
2=188
21,62=0,403 Ω
(Remarque :
Xs=lsω
avec
ω=2πf
)
Exercice IV
On considère un transformateur monophasé dont les essais préliminaires ont donné :
•à vide : V1 = V1n = 220 V, I1 = 0,5 A, V2 = 110 V, puissance absorbée : 50 W
•en court-circuit : V1 = 21 V, I2 = 20 A, puissance absorbée : 150 W
3. Proposer un montage permettant de réaliser
les mesures en court-circuit.
4. Déterminer les éléments du schéma
équivalent ci-contre :
wwwwwwwwwwwwwwwwwwwwwwwwwww
w
X
s
R
s
m
L
R
f
La démarche est identique à celle de l'exercice précédent : on utilise successivement les résultats de l'essai à
vide pour déterminer
m
,
Rf
,
L
puis de l'essai en court circuit pour déterminer
Rs
et
Xs
.
Essai à vide :
m=V20
V1
=110
220 =0,5
Les puissances apparente
S0
, active
P0
et réactive
Q0
sont reliées par
S0
2=P0 2+Q0 2
avec
S0=V1.I10=220×0,5=110 VA
Ce qui donne
Q0=
√
S0
2– P0 2=
√
1102–502=98 var
La résistance
Rf
« consomme » la puissance active
P0
ce qui permet d'écrire
P10=V1
2
Rf
et donc
Rf=V1
2
P10
=2202
50 =968 Ω
L'inductance
L
« consomme » la puissance réactive
Q0
ce qui permet d'écrire
Q10=V1
2
Lω
et donc
L=V1
2
Q10 ω=2202 98×2π50 =1,57 H
(remarque :
ω=2pi f
et f = 50 Hz)
Essai en court circuit (les influences de
Rf
et
L
sont négligées)
Les puissances apparente
Scc
, active
Pcc
et réactive
Qcc
sont reliées par
Scc
2=Pcc 2+Qcc 2
avec
Scc=V1cc .I1cc
. Pour calculer
I1cc
, on utilise la relation pour les courants du transformateur parfait :
I1cc=m I2cc=0,5×20=10 A
Ce qui donne
Scc=21×10=210 VA
et
Qcc=
√
Scc
2– Pcc 2=
√
21002–1502=147 var
c. Calculer Rs et Xs.
La résistance
Rs
« consomme » la puissance active
Pcc
ce qui permet d'écrire
Pcc=RsI2cc
2
et donc
Rs=Pcc
I2cc
2=50
202=0,375 Ω
Transformateurs monophasés Page 2 TS1 ET 2013-2014

La réactance
Xs
« consomme » la puissance réactive
Qcc
ce qui permet d'écrire
Qcc=XsI2cc
2
et
donc
Xs=Qcc
I2cc
2=147
202=0,367 Ω
(Remarque :
Xs=lsω
avec
ω=2πf
)
Pour la suite, le transformateur est supposé parfait pour les courants lorsqu’ils sont proches de leurs valeurs
nominales. On branche au secondaire une résistance Rc = 5 W en série avec une inductance Lc = 11 mH.
5. Représenter le schéma permettant de déterminer l’intensité dans la charge et la tension à ses bornes.
Le schéma « complet » est représenté ci-dessous, seule la partie « secondaire » (à droite du transformateur
parfait) est utile pour cette question.
Xs=lsω
et
rs=Rs
6. Calculer l’intensité efficace du courant secondaire.
La loi des mailles appliquée au circuit secondaire permet d'écrire :
−mV 1– RsI2– j X sI2−RcI2– j LcωI2=0
soit
−mV 1=(Rs+Rc+j(Xs+Lcω)) I2
(Remarque : cette équation peut être obtenue directement en
appliquant les lois d'association des impédances et la loi d'Ohm).
Finalement :
I2=−mV 1
Rs+Rc+j(Xs+Lcω)
et la valeur efficace du courant secondaire est égale au module
du nombre complexe
I2
associé à l'intensité secondaire soit
I2=mV 1
√
(Rs+Rc)2+( Xs+Lcω)2
I2=0,5×220
√
(0,375+5)2+(0,367+11.10−32π50)2=16,7 A
7. Calculer le déphasage entre l’intensité et la tension au secondaire.
Sur un diagramme vectoriel, l'intensité secondaire est choisie comme origine des phases et placée
horizontalement. Le vecteur associé à la tension aux bornes de
Rc
est colinéaire et de même sens que
celui associé à l'intensité alors que le vecteur associé à la tension aux bornes de
Lc
est en avance de 90°
sur celui associé à l'intensité. La tangente du déphasage entre l’intensité et la tension au secondaire est
donnée par
tan ϕ2=Lcω
Rc
=11.10−32π50
5=0,691
soit
ϕ2=34,6 °
Transformateurs monophasés Page 3 TS1 ET 2013-2014

8. Tracer le diagramme de Fresnel permettant de déterminer la valeur efficace de la tension aux bornes de la
charge.
Le diagramme est représenté ci-contre. Tous les « I »
et les « V » devraient être soulignés car il s'agit de
nombres complexes.
Démarche :
•Placer
I2
horizontalement
•Placer
RsI2
et
j XsI2
•Tracer l'arc de cercle partant de l'origine du
diagramme (origines de
RsI2
et
j XsI2
) et
de rayon
V20=mV 1
•Tracer l'horizontale partant de l'extrémité de
RsI2+j XsI2
et la portion de droite partant de
cette même extrémité et faisant un angle de 34,6°
avec l'horizontale.
•Le talon du vecteur
V2
est à la pointe de
RsI2+j XsI2
et sa pointe est sur l'arc de
cercle de rayon
V20
:
sa valeur efficace est égale à 109 V
9. Déterminer graphiquement l’intensité efficace du courant primaire.
L'intensité efficace de
I1t
(voir le schéma) est calculée à partir de
I1t =m I2=0,5×16,7=8,35 A
Les intensités efficaces des courants
I1f
et
I1m
(voir le schéma) sont calculées à partir des valeurs de
Rf
et
L
trouvées à la question 2 :
I1f=V1
Rf
=220
968 =0,23 A
et
I1m=V1
Lω=220 1,57×2π50 =0,45 A
Ces deux valeurs sont très faibles devant
I1t
, on peut donc admettre
I1=I1t
Exercice V
On considère un transformateur monophasé sur lequel les essais suivants ont été effectués :
•en continu au primaire : I1c = 10 A ; U1c = 5 V.
•à vide : U1 = 220 V, 50 Hz (tension primaire nominale) ; U20 = 44 V ; P10 = 80 W ; I10 = 1 A.
•en court-circuit : U1cc = 40 V ; P1cc = 250 W ; I1cc = 20 A (courant nominal primaire).
Le transformateur est considéré comme parfait pour les courants lorsque ceux-ci ont leurs valeurs nominales.
3. Exploitation de l'essai à vide
c. Déterminer le rapport de transformation.
On utilise l'essai à vide :
m=U20
U1 =44 220 =0,2
d. En déduire le nombre de spires au secondaire si l’on compte 520 spires au primaire.
Puisque
m=n2
n1
alors
n2=m×n1=0,2×520=104 spires
e. Vérifier que l’on peut négliger les pertes par effet Joule lors de l’essai à vide.
Les pertes par effet Joule lors de l’essai à vide sont localisées dans la résistance de l'enroulement du primaire.
Transformateurs monophasés Page 4 TS1 ET 2013-2014

On peut déterminer cette résistance à partir de l'essai en continu soit
r1=U1c
I1c
=5
10 =0,5 Ω
.
L'intensité efficace du courant primaire est égale à 1 A ce qui donne des pertes par effet Joule égales à
Pj0=r1I10
2=0,5×12=0,5 W
. Cette valeur est bien négligeable devant 80 W.
4. Exploitation de l'essai en court-circuit
c. En admettant que les pertes dans le fer sont proportionnelles au carré de la tension primaire, montrer
qu’elles sont négligeables par rapport aux autres pertes de l’essai en court-circuit.
D'après l'énoncé
P10=K U1
2
(D'après le cours
P10=1
Rf
U1
2
ce qui donnerait
K=1
Rf
). L'essai à
vide permet de calculer
K=P10
U1
2=80
2202=1,65 .10−3 S
ce qui donne des pertes dans le fer lors de l'essai
en court-circuit :
Pfcc=1,65 .10−3×402=2,6 W
. Cette valeur est négligeable devant 250 W.
d. Représenter le schéma équivalent du transformateur en court-circuit vu du secondaire.
Les influences des impédances placées au primaires (
Rf
et
Lm
du cours) sont négligées et remplacées
par des circuits ouverts.
rs=Rs
et
lsω=Xs
e. En déduire les valeurs de Rs et Xs de l’impédance du modèle de Thévenin.
Calcul de l'intensité du courant secondaire en court-circuit :
I2cc=1
mI1cc=1 0,2 ×20=100 A
La résistance
Rs
« consomme » la puissance active
P1cc
ce qui permet d'écrire
P1cc=RsI2cc
2
et
donc
Rs=P1cc
I2cc
2=250
1002=25 mΩ
La réactance
Xs
« consomme » la puissance réactive
Q1cc
qu'il faut calculer :
Q1cc=
√
S1cc
2– P1cc 2=
√
(40×20)2–2502=760 var
ce qui permet d'écrire
Q1cc=XsI2cc
2
et donc
Xs=Q1cc
I2cc
2=760
1002=76 m Ω
5. Quels que soient les résultats obtenus précédemment, on prendra pour la suite du problème Rs = 25 mW ;
Xs = 75 mW. Le transformateur alimenté au primaire sous sa tension nominale, débite 100 A au secondaire
avec un facteur de puissance égal à 0,9 (charge inductive).
c. Déterminer graphiquement la tension secondaire du transformateur. En déduire la puissance délivrée par
le secondaire. Faire le même calcul avec l’approximation du triangle fondamental de Kapp.
Le déphasage entre la tension et le courant secondaires est déterminé à partir du facteur de puissance :
cosϕ2=0,9
donne
ϕ2=26 °
ou
ϕ2=−26 °
; comme la charge est inductive alors le courant est
Transformateurs monophasés Page 5 TS1 ET 2013-2014