Corrigé 1) En régime continu, il n`y a pas de chute de tension dans

page 1/2
TRANSFO34
Des essais sur un transformateur ont donné :
Essai en CONTINU Essai à VIDE Essai en Court Circuit
Au primaire: U
1V
= 230V I
2CC
= 9,1 A
U = 6,0V et I = 1,0A I
lV
= 0,11 A U
lCC
= 20 V
U
2V
= 25,3 V
P
lV
= 6,9 W P
lCC
= 11 W
Les tensions et intensités indiquées sont des valeurs efficaces.
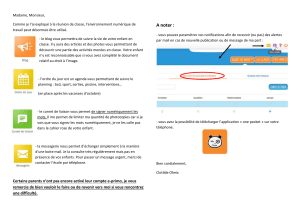
En supposant le circuit magnétique linéaire, le modèle équivalent du transformateur est le suivant.
1) Déterminer numériquement la résistance R
1
et le rapport de transformation m.
2) Donner le modèle équivalent du transformateur vu du secondaire, en faisant apparaître une résistance R
S
et une inductance L
S
.
3) À l'aide des résultats de l'essai à vide, déterminer numériquement :
a) les pertes par effet joule à vide P
JV
;
b) les pertes dans le fer P
FV
;
c) le facteur de puissance à vide cos(ϕ
V
). Commenter.
4) À l'aide des résultats de l'essai en court circuit, déterminer numériquement:
a) la résistance R
2
.
b) L’inductance des enroulements ramenée au secondaire L
S
.
Corrigé
1) En régime continu, il n’y a pas de chute de tension dans des inductance des enroulements
donc on a U = R
1
I. A.N. R
1
6
0
1 0
=
,
, = 6
Ω .
Le transformateur est parfait pour les tensions dans son fonctionnement à vide donc
m
U
U
=
2
1
V
V
. A.N. m=
25
3
230
,
= 0,11.
2) En régime sinusoïdal, on peut écrire les loi d’Ohm au primaire et au secondaire :
U
1
= R
1
I
1
+ jL
1
ωI
1
+ U
1PARF
;
U
2
= R
2
I
2
+ jL
2
ωI
2
+ U
2PARF
;
Comme les courants i
1
et i
2
traversent le
transformateur parfait, on a la relation
I
I m
2
1
1
= − avec les orientations indiquées. De même, on a
U
Um
2
1
PARF
PARF
= avec les orientations indi-
quées.
On reportant, on obtient U
2
= R
2
I
2
+jL
2
ωI
2
+ m[U
1
– (R
1
+jL
1
ω)(–m)I
2
]
= mU
1
+ (R
2
+ m
2
R
1
)I
2
+j(L
2
+ m
2
L
1
)ωI
2
.
En posant R
S
= R
2
+ m
2
R
1
et L
S
= L
2
+ m
2
L
1
, on obtient la relation
U
2
= mU
1
+ R
S
I
2
+jL
S
ωI
2
qui correspond au schéma suivant:
3-a) Dans le fonctionnement à vide, il n’y a pas de courant dans le secondaire donc les per-
tes par effet Joule à vide sont P
J,V
= R
1
.I
1V2
. A.N. : P
J,V
= 6.(0,11)
2
= 73 mW.
b) La puissance absorbée par le primaire est P
1V
= P
J,V
+ P
F,V
d’où P
F,V
= P
1V
- P
J,V
.
Or la question précédente montre que P
J,V
<< P
1V
donc il reste P
F,V
= P
1V
.
A.N. P
F,V
= 6,9 W.
c) La puissance moyenne s’écrit P
1V
= U
1V
.I
1V
cos(ϕ) donc cos( )ϕ
VV
V 1V
=
P
1
1
U I .
m
u
1
u
2
R
2
L
2
R
1
L
1
u
1 u
2
m
u
1
u
2
R
2
L
2
R
1
L
1
u
1PARF
u
2PARF
i
1
i
2
mu
1
R
S
L
S
u
2

page 2/2
A.N. cos( )
,
( )( , )
ϕ
V
=
6
9
230 0 11 = 0,27.
Le facteur de puissance est faible car le transformateur à vide se comporte comme une bo-
bine à noyau de fer et le courant est pratiquement en quadrature avec la tension.
4-a) Dans l’essai en court-circuit, il n’y a pas de charge donc toute la puissance fournie par
la source est absorbée dans la résistance R
S
car l’inductance n’absorbe pas de puissance. On a donc
P
1CC
= R
S
I
2CC2
d’où, numériquement, R
S
=
11
9 1
2
( , ) = 0,133 Ω.
On en déduit alors R
2
= R
S
– m
2
R
1
. A.N. R
2
= 0,133 – (0,11)
2
(6) = 0,06 Ω.
b) Dans l’essai en court-circuit, on a u
2
= 0 donc (R
S
+jL
S
ω)I
2
= –mU
1
d’où
R L
mU
I
S S CC
2CC
221
+ =( )ω en prenant le module. On en déduit LmU
IR
SCC
2CC
S
=
F
H
G
I
K
J
−
1
1
2
2
ω.
A.N. L
S
=
F
H
G
I
K
J
−
1
2 50
0 11 20
9 1 0 133
2
2
π( )
( , )( )
,( , ) = 0,64 mH.