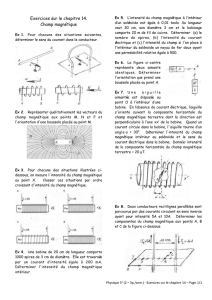
énoncé

Spé ψ 2011-2012 page 1/6 Devoir n°2
Spé ψ 2011-2012 Devoir n°2
ÉLECTROMAGNÉTISME
Partie I
DISTRIBUTIONS ORTHORADIALES DE COURANT ÉLECTRIQUE.
On cherche à déterminer le champ magnétique créé par diverses distri-
butions orthoradiales de courant électrique continu circulant dans un cylindre
de rayon a et de hauteur H.
On suppose que a est très petit devant H (a << H) ; de ce fait :
y On négligera les effets de bords ( ce qui revient à considérer le
cylindre comme illimité dans la direction z).
y Le champ magnétique EXT
B
J
G à l’extérieur du cylindre est nul.
On utilisera les coordonnées cylindriques
(
)
,,rz
θ
et la base
(
)
,,
rz
eee
θ
G
GG.
Dans toute la suite, on considérera que les propriétés électromagnétiques de l’air sont identi-
ques à celles du vide.
Les données sont : a, H et la perméabilité du vide μ0 .
I-1°) Distribution volumique orthoradiale de courants
Le courant électrique circule dans le cylindre ; la densité de courant volumique en un point
M(r, θ, z) intérieur au cylindre est : 1 Jre
θ
=α
JGG
; elle n’est donc pas uniforme. Cette distribution
crée, au point M, le champ magnétique 1
B
J
G .
a) Par des considérations qualitatives précises, déterminer la direction de 1
B
JG puis la
(ou les) coordonnée(s) dont dépend la valeur algébrique B1 de ce champ.
b) Déterminer B1 en fonction de α, r et des données, pour tout r inférieur ou égal au
rayon a .
I-2°) Distribution surfacique orthoradiale.
À présent, le courant électrique ne circule que sur la surface latérale du cylindre, l’intérieur
étant « vide ». Il est caractérisé par le vecteur densité de courant surfacique SS JJe
θ
=
JG G , JS étant uni-
forme et constant. Cette distribution crée, à l’intérieur, le champ 0
B
J
G ( rappelons que EXT
B
JG est nul ).
a) Montrer qu’un champ uniforme 0
B
J
G satisfait aux équations de Maxwell à
l’intérieur du cylindre.
b) Rappeler les relations de passage relatives aux composantes du champ magnétique
à une interface.
c) En déduire l’expression de 0
B
J
G.Partie II
FOUR À INDUCTION.
Un four à induction est constitué d’une bobine cylindrique formée
de N spires régulièrement espacées, de rayon a, réparties sur une couche de
hauteur H noyée dans une matrice réfractaire. Un courant électrique
d’intensité
() ( )
mcosit I t=ω circule dans chaque spire.
On se place dans le cadre d’un régime électromagnétique quasi
stationnaire : les expressions des champs trouvées à la question I restent
valables.
II-1) Champ magnétique à l’intérieur du four « vide »
r
z
e
G
z
H
r
e
G
e
θ
⊗
G
a
z
e
G
a
H
z
z
’
i
i

Spé ψ 2011-2012 page 2/6 Devoir n°2
On assimile cette distribution de courant formée par les N spires à une distribution surfaci-
que orthoradiale de courant, de densité surfacique SS JJe
θ
=
J
GG
, JS étant uniforme. Les données sont :
N, i, H, a, μ0.a) Évaluer JS en fonction de i, N et H.
b) Déterminer le champ magnétique 0
B
J
G à l’intérieur. On met sa valeur algébrique
sous la forme
()
0m
cos
B
KI t=ω ; donner l’expression de K.
II-2) Terme principal du champ électromagnétique du four « chargé ».
L’intérieur de la bobine est complètement rempli du matériau non ferreux à fondre. Dans la
suite, on fera les hypothèses suivantes :
y Ce matériau est conducteur électrique : il obéit localement à la loi d’Ohm avec la
conductivité électrique γ constante et uniforme.
y Les champs électrique et magnétique dans le matériau obéissent aux mêmes équa-
tions de Maxwell que dans le vide sauf la relation de Maxwell-Ampére qui s’écrit :
()
00
rot E BJ
t
⎡⎤
∂
=μ +ε
⎢⎥
∂
⎣⎦
JG
JJG JG JG. On est en régime électromagnétique quasi stationnaire.
On néglige le champ magnétique crée par les courants induits, de sorte que le champ ma-
gnétique dans le matériau vaut 0
B
JG (avec
(
)
0m
cos
B
KI t
=
ω trouvé en II-1°b ) .
Les données sont K, a, H, Im, γ et α.
a) On cherche le champ électrique induit en un point M du matériau à la distance r de
l’axe de la bobine sous la forme
(
)
11,EErte
θ
=
JG G . En exprimant la circulation de 1
E
JG sur un contour
que l’on précisera, trouver
()
1,Ert en fonction de r, t et des données.
b) Rappeler la loi locale d’Ohm. En déduire l’expression de la densité volumique de
courant induit 1
J
JG au point M.
II-3) Puissance transférée.
a) Donner l’expression de la puissance volumique locale pV cédée par le champ
électrique aux porteurs de charge.
b) Évaluer la puissance instantanée totale transférée au matériau conducteur contenu
dans le four. c) En déduire la puissance moyenne P (on donnera l’expression en fonction des don-
nées et du volume V occupé par le matériau ). Montrer que le modèle explique pourquoi dans le
chauffage par induction, on choisit une fréquence de 20 kHz plutôt que le 50 Hz directement acces-
sible.
d ) On évalue les fuites énergétiques par rayonnement à η = 15% de l’énergie requise
pour la fusion. Déterminer littéralement puis calculer numériquement la durée τf de cette fusion ; on
donne : f = 4000 Hz ; Im = 150 A ; K = 10–5 T⋅A–1 ; a = 15 cm ; γ = 1,6×106 S⋅m–1 ; l’enthalpie
massique de fusion du matériau est ΔhFUS = 350 kJ⋅kg ; Au départ, le matériau est solide à la tempé-
rature de fusion ; sa masse est M = 80kg et il occupe un volume V = 0,03 m3 supposé quasi invariant
pendant toute la fusion. Partie III
ALIMENTATION ÉLECTRIQUE DU FOUR À INDUCTION.
III-1) On maintient une tension u = Um cos(ωt) aux bornes d’une bobine inductive de résis-
tance R et d’auto-inductance L. L’intensité du courant électrique est alors i = Im cos(ωt + ϕ).
Les données sont : L, R, Um. Pour les applications numériques, on prendra :
R = 100 Ω ; Lω = 400 Ω lorsque f = 4000 Hz ; Um = 1,50V .
a) Déterminer littéralement :

Spé ψ 2011-2012 page 3/6 Devoir n°2
y l’amplitude Im et la valeur efficace IEFF , en fonction de ω et des données ;
y la puissance électrique moyenne P transférée à la bobine ;
y la valeur maximale PMAX de P, pour R, L et Um fixés ;
b) Déterminer littéralement le taux de transfert de puissance MAX
TP /=PP puis cal-
culer numériquement sa valeur pour la fréquence f = 4000 Hz.
III-2) On ajoute un condensateur de capacité C en série avec la bobine précédente. Cet en-
semble est alimenté par la tension précédente u = Um cos(ωt).
a) Donner l’expression littérale du taux de transfert TP, PMAX étant le même qu’en
III-1-a et P la puissance moyenne fournie par la source d’alimentation.
b) Établir l’expression littérale de la valeur C0 de C permettant un transfert optimal
de puissance électrique à la bobine, à la fréquence imposée f = 4000 Hz. Calculer numériquement
C0 et TP(C0). Conclure.
c) Tracer, après une étude asymptotique, une représentation graphique de TP en
fonction de C.
d) Lorsque C = C0, donner l’expression littérale de Im et ϕ.
III-3) On réalise le circuit ci contre, avec Um = 1,50 V, r = 30 Ω
et f = 4000 Hz. La sensibilité verticale sur les deux voies est de
0,5 V/division.a) La bobine étant « vide », on règle la valeur de la capa-
cité à C = 37,5 nF pour obtenir l’oscillogramme n°1 (rappel : VPP est la
tension crête à crête). Déduire de l’oscillogramme n°1 les valeurs de la
résistance RV de cette bobine et de son inductance « à vide » LV lors-
que la bobine est « vide ».
b) On insère un morceau d’aluminium (substance non ferreuse) dans la bobine ; on
observe alors un décalage des courbes ( oscillogramme n°2 ). Déterminer le déphasage de i par rap-
port à u.
VPP(1) = 1,734 V ;
VPP(2) = 3,000 V ;
f = 4000 Hz ;
base de temps: 50μs/division
Oscillogramme n° 1
i
Y2
u = U
m
cos
(
ω
t
)
Y1
C
r
GBF Bobine
VPP(1) = 0,470 V ;
VPP(2) = 3,000 V ;
f = 4000 Hz ;
base de temps: 50μs/division
Oscillogramme n°2

Spé ψ 2011-2012 page 4/6 Devoir n°2
c) Pour obtenir l’oscillogramme n°3, on doit faire passer la capacité à la valeur
C’ = 43,7 nF. Déterminer les valeurs de sa résistance RC et de son inductance LC lorsque la bobine
contient un morceau d’aluminium.
III-4) La charge mise à fondre dans le four change les paramètres électriques R et L de ce
four. En particulier, l’inductance L baisse en cours de chauffe. On désire que le four travaille cons-
tamment à puissance optimale. Dans la pratique, on choisit C de manière à optimiser le transfert de
puissance « à froid », puis on régule en cours de chauffe en jouant sur un autre paramètre. Préciser
quel est ce paramètre et quel doit être le sens de son évolution en cours de chauffe. Justifier votre
réponse.
Partie IV
ÉTUDE DES COURANTS DE FOUCAULT
Dans cette partie est proposée une autre modélisation qui permettra d’exprimer la puissance
dissipée par les courants de Foucault de la plaque.
IV-A - Modélisation
IV.A.1) On considère une spire de rayon R parcourue par un courant I. On note O son centre
et Oz son axe et on travaille en coordonnées cylindriques d’ axe Oz.
a) Montrer par des considérations de symétrie et d’invariance clairement explicitées
que le champ magnétique en un point
(
)
,,
M
rzθ quelconque de l’espace s’écrit :
(
)
(
)
(
)
rZ
rz
,,
B
M B rzu B rzu=+
JG G G
b) On se limite ici aux points de l’axe . Après avoir précisé la direction du champ
dans ce cas particulier, l’exprimer en fonction de z, R et I.
IV.A.2) On assimile le matériau conducteur à une plaque métallique cylindrique de rayon a,
d’épaisseur e. Cette plaque est posée au-dessus de l’inducteur (voir figure 1).
On supposera pour simplifier que l’inducteur est une bobine plate constituée de N spires de
rayons voisins pris tous égaux à R, chacune parcourue par un courant I. On supposera que l’on s’est
placé dans des conditions telles que le champ magnétique créé par l’inducteur au niveau de la base
inférieure de la plaque avant qu’on ne mette la plaque, peut être considéré comme uniforme, égal à
celui que créeraient les spires en leur centre. Dans toute cette partie, on prendra comme origine de
l’axe des z, le point Ω centre de la base inférieure de la plaque (voir figure 2).
La plaque est constituée d’acier magnétique de conductivité électrique γ. On supposera ici
que cet acier est un milieu magnétique linéaire, homogène et isotrope de perméabilité magnétique
μ, c’est à dire que les équations de Maxwell dans ce milieu s’écrivent :
Oscillogramme n° 3
VPP(1) = 1,078 V ;
VPP(2) = 3,000 V
f
= 4000 Hz
base de temps: 50μs/division

Spé ψ 2011-2012 page 5/6 Devoir n°2
()
[]
()
[]
()
[]
()
[]
0
div 0 .1 rot .2
div 0 .3 rot .4
B
EM E M
t
E
BM BJ M
t
∂
==−
∂
∂
==μ+εμ
∂
J
G
JG J JG JG
JG
JG J J G JG JG
avec E
JG champ électrique,
B
JG champ magnétique dans le milieu, J
J
G vecteur densité volumique de
courant et μ=μ0μr, perméabilité magnétique de l’acier. On supposera en outre que la loi d’Ohm lo-
cale est vérifiée dans l’acier.
Données : N = 10 ; R = 16,0 cm ; a = 4,0 cm ; e = 5,0 mm ; I = 5,0 A ; γ = 5,0×106 Ω–1⋅m–1 ;
μr = 100 ; 09
1
36 10
ε= π F⋅m–1 ; μ0 = 4π×10–7 H⋅m–1.
a) Quelle équation de Maxwell permet d’affirmer qu’il y a continuité de la compo-
sante normale de
B
JG à l’interface entre le vide et les bases inférieures et supérieures de la plaque
étudiée ?
Étant constituée d’acier magnétique, la plaque s’aimante et modifie à son tour le champ ma-
gnétique dans le vide. On supposera dans la suite que ce phénomène et le respect de la continuité
vue en ci-dessus donnent pour valeur de la composante normale de
B
J
G au niveau de la base infé-
rieure de la plaque (en z = 0+), la valeur du champ créé en ce point dans le vide avant introduction
de la plaque multipliée par une constante appelée perméabilité relative μr de la plaque.
b) Écrire
()
,, 0
z
Br z + θ= , composante axiale du champ magnétique au niveau de la
base inférieure de la plaque en fonction de N, R, I, μ0 et μr.
IV.B - Calcul des courants de Foucault dans la plaque
Le courant circulant dans l’inducteur est maintenant sinusoïdal de fréquence f = 20 kHz :
() ( )
cosit I t=ω
avec ω = 2πf.
Comme on se limitera à l’étude du régime sinusoïdal établi, on pourra utiliser les représen-
tations complexes des grandeurs. Ainsi, à tout champ vectoriel
(
)
,,,Ar ztθ
J
G dans la plaque, on as-
sociera it it it
rz
rz
A
Ae e Ae e Ae e
ωωω
θ
θ
=++
JG G G G , où i2 = –1 et
(
)
Re
A
A=
J
GJG
; r A, Aθ, z A sont des fonc-
tions complexes des seules variables r, θ et z.
IV.B.1) Montrer que pour la fréquence utilisée, l’équation de Maxwell-Ampère [M.4] peut
être simplifiée. Donner le nom de l’approximation ainsi faite. Dans toute la suite, on travaillera avec
la forme simplifiée.
IV.B.2) Montrer que J
JG vérifie l’équation différentielle : 0Ji J
Δ
−γωμ =
J
JJG
J
GJGG (5)
IV.B.3) Donner des arguments qui permettent de justifier que l’on cherche les courants in-
duits dans la plaque sous la forme :
(
)
,it JJrzee
ω
θ
=
JGG
.
I
Inducteur (N spires)
a
z
ePlaque Ω
figure 1 figure 2