Inégalités et pauvreté, de Pareto à Galbraith

Colloque « Inégalités et pauvreté dans les pays riches », IUFM Auvergne, Chamalières, 20 janvier 2012
1
Inégalités et pauvreté, de Pareto à Galbraith
Débats et controverses
(Version provisoire)
Arnaud DIEMER
Université Blaise Pascal, TRIANGLE, CERDI
Le début du XIXe siècle a introduit une rupture épistémologique importante. L’économie
politique fait ses premiers pas et très vite, elle s’engage dans une démarche scientifique.
David Ricardo et Robert Malthus insistent notamment sur les lois générales, nécessaires et
universelles du marché. La loi de l’offre et la demande s’applique à toutes les marchandises, y
compris la terre, la monnaie et le travail. Dans ces conditions, les lois de l’économie peuvent
être mobilisées pour analyser et solutionner un grand nombre de questions sociales
(Lallement, 2010). L’une d’entre elles va focaliser l’attention des économistes, c’est la
question de la pauvreté. David Ricardo et Robert Malthus (mais également John Locke en son
temps) vont s’engager dans une véritable croisade contre les lois sur les pauvres (la fameuse
loi de Speenhamland), accusées de favoriser les mariages imprudents, de provoquer une
fécondité élevée et un dysfonctionnement du marché du travail (Diemer, Guillemin, 2010).
L’abrogation de cette loi en 1834 peut être présentée comme une victoire pour ces
économistes libéraux, fervents défenseurs de la loi du marché. Elle marque selon Karl Polanyi
(1944), l’avènement du système capitalisme et la naissance d’un véritable marché du travail.
Si la lutte contre la pauvreté devient une question de théorie économique, elle connaîtra une
certaine inflexion dans la seconde moitié du XIXe Siècle, les travaux d’Auguste et Léon
Walras, puis ceux de Vilfredo Pareto vont progressivement nous faire entrer dans la sphère de
la répartition de la richesse, un domaine longtemps resté au second plan des recherches
économiques et des préoccupations des économistes (Knight, 1956, Busino, 1965) :
« Résoudre la question de l’organisation économique de la société, ce serait, en somme, déterminer les
conditions : 1) de la production la plus abondante possible et 2) de la répartition la plus équitable possible de la
richesse sociale entre les hommes en société » (Walras L., 1896, p. 175).
« L’influence des lois économiques sur la répartition des richesses est un sujet beaucoup moins exploré que
l’influence des mêmes lois sur la circulation. On remplirait des salles entières des innombrables traités sur la
production, sur les banques, sur l’échange. Au contraire, le problème si grave de la distribution des richesses ne
tient en général qu’un place médiocre, secondaire, dans les livres d’économie politique et il n’a guère été l’objet
de longs traités que de la part d’écrivains appartenant à l’école sentimentale ou socialiste » (Pareto, 1881, p.

Colloque « Inégalités et pauvreté dans les pays riches », IUFM Auvergne, Chamalières, 20 janvier 2012
2
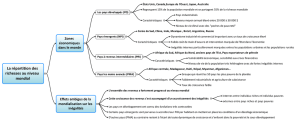
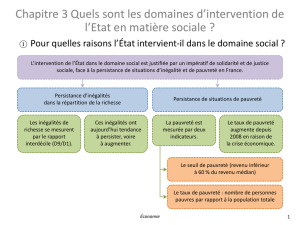
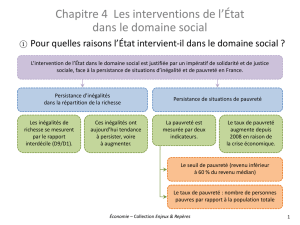
Le papier se propose d’analyser les inégalités et la pauvreté sous l’angle de la répartition
des richesses en prenant comme toile de fond une histoire longue des faits et des idées
économiques. Ce type d’exercice est toujours périlleux, car il amène souvent celui qui s’y
livre, à formuler une énième histoire de la pensée économique, sortie de tout contexte et basée
sur des clés, fort discutables. L’histoire que nous évoquons ici, à un point de départ, les
travaux de Pareto sur la répartition des revenus et de la fortune. Ces travaux vont bénéficier de
la multiplication et du perfectionnement des données statistiques. A la fin du XIXe siècle, un
grand nombre de gouvernements (Allemagne, Angleterre, France, Prusse, Suisse…) se sont
dotés d’un recueil de statistiques qui remet au devant de la scène, l’observation des faits.
L’analyse des inégalités et de la pauvreté rentre ainsi dans l’ère de la mesure. Il s’agit d’une
part, d’observer et de saisir des données, puis d’autre part, de trouver une méthode
d’interpolation permettant d’homogénéiser ces données. Une loi empirique peut être ainsi
déduite de ce travail, c’est la fameuse loi de Pareto. Cette histoire a également un point de
rupture, c’est la crise de 1929, la Grande Crise, qui met sur le devant de la scène, un
phénomène nouveau, le chômage de masse. La question des inégalités et de la pauvreté est
dès lors rattachée au problème du sous-emploi et sa formulation pose le problème des
solutions qu’il convient d’apporter à des faits cumulatifs (perte d’emploi, perte de revenus,
perte de la protection sociale, perte du logement…). Keynes (1936) proposera dans sa théorie
générale, une solution visant à recréer les conditions du plein emploi et à réduire certaines
inégalités. En effet, les inégalités ne sont pas toutes bonnes à réduire. Pour certaines, elles
renvoient à la nature humaine et doivent donc être traitées en tant que telles. De son côté,
Maurice Allais (1946) cherchera à introduire une troisième voie, la planification
concurrentielle, entre le laisser faire manchestérien et la planification autoritaire. Cette voie
pose le principe de la concurrence organisée et donne à l’Etat, un rôle important, celui
d’encadrer le marché. Le problème de la répartition de la richesse est au cœur de la
discussion. Cependant, tout en proposant d’atténuer les inégalités, Maurice Allais note
qu’elles font partie de notre organisation économique et sociale, elles sont la conséquence de
sa théorie des élites (un principe de sa justice sociale). Enfin, Galbraith (1961, 1980) suggère
d’aborder la question de la pauvreté de masse sous l’angle de l’équilibre circulaire et de
l’accommodation. En comparant l’analyse de la pauvreté dans les pays riches et les pays
pauvres, Galbraith nous propose une approche sociologique susceptible d’expliquer des
phénomènes tels que les trappes à pauvreté, les migrations des élites, le chômage de masse.
I. Vilfredo Pareto, l’ère de l’observation et de la mesure
Lorsque l’on aborde la question des inégalités dans l’approche parétienne, on a coutume de
faire référence à l’Optimum de Pareto, c'est-à-dire à un état dans lequel il n’est pas possible
d’améliorer la satisfaction d’un agent sans détériorer celle d’un autre agent. Notons
rapidement que le fait d’atteindre l’optimum de Pareto ne préjuge cependant pas d’une
distribution « égale » des revenus. En effet, il existe une infinie d’optima de Pareto qui
peuvent correspondre à des répartitions très différentes des ressources (revenus) entre les
agents économiques (tout dépend de leurs dotations initiales, une hypothèse évacuée dans le
modèle de Debreu, 1959). Ainsi l’optimum de Pareto peut être compatible avec un degré plus
ou moins élevé d’inégalité. Ce qui a permis à certains économistes (Clark, 1899) de préciser
qu’une telle situation était juste dans la mesure où chaque facteur de production était
rémunéré à sa productivité marginale. Cette histoire, qui est généralement rappelée dans tous
les manuels et ouvrages abordant ce que l’on a coutume d’appeler la théorie du bien être,
réduit la portée des travaux de Pareto et notamment son analyse de la pauvreté et des
inégalités. Elle minimise d’une part, la méthodologie employée et d’autre part, l’ambition de

Colloque « Inégalités et pauvreté dans les pays riches », IUFM Auvergne, Chamalières, 20 janvier 2012
3
Vilfredo Pareto. Dans ce qui suit, nous chercherons à mettre en valeur les apports de Vilfredo
à l’analyse des inégalités et de la pauvreté.
Succédant à Léon Walras à la chaire d’économie politique de Lausanne, Vilfredo Pareto
s’est proposé de « rechercher les uniformités que présentent les phénomènes [économiques et
sociaux], c'est-à-dire leurs lois » (1909, [1966, p. 2]). Quiconque étudie une science sociale
doit admettre implicitement l’existence de ces uniformités. Toutefois, rappelle Pareto,
l’imperfection de notre esprit ne nous permet pas de considérer les phénomènes dans leur
ensemble. Nous sommes donc obligés de les étudier séparément, « de considérer un nombre
infini d’uniformités partielles, qui se croisent, se superposent et s’opposent de mille
manières » (1909, [1966, p. 8]). Ainsi, si l’analyse des inégalités et de la pauvreté renvoie à la
théorie de l’hétérogénéité sociale, la répartition des revenus n’en constitue qu’un cas
particulier. L’expérience et l’observation révèlent que la répartition des revenus varie peu
dans l’espace et dans le temps pour les peuples civilisés. Par déduction, deux théorèmes sont
présentés : (1) la répartition des richesses n’est pas le fruit du hasard ; (2) pour relever le
niveau du revenu minimum et réduire l’inégalité des revenus, il faut que la richesse croisse
plus vite que la population. Ainsi l’amélioration des conditions des classes pauvres est avant
tout un problème de production, et non de répartition de la richesse. Les apports de la
sociologie et de l’anthropologie nécessitent cependant de dépasser le cadre des lois
économiques pour introduire la mutuelle dépendance des phénomènes économiques et des
phénomènes sociaux. L’hétérogénéité sociale conduit à rechercher l’équilibre social du côté
de la théorie de la circulation des élites.
A. La courbe de répartition des revenus
La première mention de la distribution des revenus apparaît en janvier 1895, dans un article
intitulé « la legge della demanda » et paru dans le Giornale degli Economisti (p. 59 – 68). Par
la suite, elle fera l’objet d’une réimpression dans les « Ecrits sur la courbe de la répartition de
richesse » publié dans les Recueils de la Faculté de Droit de Lausanne (1896, p. 371 - 387),
pour finalement constituer le premier chapitre du livre III « La répartition et la
consommation » du Cours d’économie politique (1897, p. 299 – 345).
Ce premier chapitre, consacré à la courbe des revenus, commence par quelques précisions
sur la notion de richesse sociale. Aux yeux de Pareto, « cette notion est un terme très vague,
qu’il est indispensable de préciser » (1897, p. 299) si l’on souhaite l’évaluer. Car ce qui
préoccupe avant tout notre ingénieur économiste
1
, c’est la possibilité d’évaluer en numéraire
la totalité des capitaux (mobiliers et fonciers) d’un pays. Or les outils statistiques de l’époque
n’offrent que peu de secours, une méthode pour estimer la richesse sociale a été proposée par
Alfred de Foville
2
, co-fondateur de l’Institut international de statistique (1885) et auteur d’un
ouvrage sur la Richesse en France et à l’Etranger (1893). Dans cet ouvrage, Alfred de Foville
recommande d’évaluer le montant total des fortunes privées en multipliant « l’importance
moyenne des successions et donations annuelles par l’intervalle moyen des mutations de ce
genre » (1893, p. 12). Cette méthode repose sur une hypothèse importante : l’intervalle moyen
ne change que lentement (en d’autres termes, la loi pour évaluer les successions et les
donations n’est pas remise en cause), de sorte que l’on peut calculer la variation de la richesse
d’un pays, à différentes époques, en comparant la moyenne des successions et des donations.
Dans le cas de la France (1879 – 1889), Alfred de Foville évalue l’intervalle moyen d’une
génération à une autre à 36 ans. Le chiffre moyen des donations et des successions étant de 6
1
Vilfredo Pareto est diplômé en ingénierie de l’Ecole Polytechnique de Turin (1870).
2
Alfred de Foville (1842 – 1913) fût surtout le chef du Bureau de statistique et de législation comparée du
ministère des Finances de 1873 à 1893.

Colloque « Inégalités et pauvreté dans les pays riches », IUFM Auvergne, Chamalières, 20 janvier 2012
4
¼ milliards, la somme fortunes privées serait de l’ordre de 225 milliards (36 x 6 ¼ si la durée
d’une génération est bien de 36 ans), soit 5570 fr par habitant. La méthode de Foville fût
appliquée en Italie par Maffeo Pantaleoni (intervalle moyen de 36 ans, fortunes privées
évaluées à 54 milliards, soit 1764 fr par habitant en 1888- 1889), dans les pays scandinaves
par Fahlbeck et Falbehausen…
A la fin du XIXe siècle, les économistes pourront compter sur les avancées en matière de
finances publiques (exemple du Cadastre en France et en Angleterre) pour évaluer la richesse
d’un pays. L’impôt sur le revenu constitue un moyen de se faire une idée des revenus des
différents capitaux (même s’il existe toujours une incertitude sur le taux de capitation). En
1885, Robert Giffen évalue la fortune de l’Angleterre à 251 milliards de francs. Sur période
longue (1855 – 1890), le calcul de l’income tax a permis de mettre en lumière les différentes
sources de revenus des anglais (diminution du revenu des terres, augmentation des revenus de
l’industrie) et de souligner que la richesse par habitant s’était considérablement accrue en un
siècle (ce cas est généralisable à l’ensemble des pays civilisés : Allemagne, France,
Belgique…). Malgré les nombreuses incertitudes associées aux déclarations des
contribuables, Pareto considère que l’impôt sur le revenu est la base la plus sûre pour
appréhender la répartition de la richesse.
La répartition de la richesse dépendrait « de la nature des hommes dont se compose la
société, de l’organisation de celle-ci, et aussi du hasard (les conjonctures de Lassalle) »
(1897, p. 304). Si l’étude des causes de la répartition de la richesse repose sur l’observation,
Pareto considère qu’il est possible de connaître cette répartition en ayant recours aux
mathématiques. Observations et lois mathématiques constitueront les deux étapes de l’analyse
d’un fait économique, en l’occurrence la répartition de la richesse. Faute d’une méthode plus
adéquate
3
, l’économiste doit se familiariser avec l’outil mathématique. Ainsi, pour un certain
revenu x, et pour le nombre de contribuables N ayant un revenu supérieur à x, il est possible
dans le cas de l’Angleterre et de l’Irlande de proposer dans le groupe Commerce et
Professions (schedule D), une classification étendue des contribuables suivant l’importance
des revenus.
Schedule D – Année 1893 – 1894
X N
En £ Angleterre Irlande
150
200
300
400
500
600
700
800
900
1000
2000
400 648
234 485
121 996
74 041
54 419
42 072
34 269
29 311
25 033
22 896
9 880
17 717
9 365
4 592
2 684
1 898
1 428
1 104
940
771
684
271
3
« Plusieurs personnes qui manquent des connaissances scientifiques nécessaires pour bien comprendre les
nouvelles théories, affirment que l’usage de mathématiques n’ajoute rien à nos connaissances en économie
politique, et elles croient le prouver en citant Cairnes. La seule preuve vraiment efficace serait de faire valoir
que l’on peut sans recourir aux mathématiques, démontrer le théorème dont nous venons de parler et bien
d’autres encore. A peine nos savants critiques auront dédaigné donner de telles démonstrations, nous ne
manquerons pas de les substituer aux nôtres. En attendant, ils voudront bien nous permettre de donner ces
démonstrations de la seule manière actuellement connue » (1897, § 962).

Colloque « Inégalités et pauvreté dans les pays riches », IUFM Auvergne, Chamalières, 20 janvier 2012
5
3000
4000
5000
10000
6 096
4 161
3 081
1 014
142
88
68
22
En portant sur l’axe des abscisses (AB), les logarithmes de x et sur l’axe des ordonnées (AC),
les logarithmes de N, Pareto note que (i) les points ainsi déterminés ont une tendance très
marquée à se disposer en ligne droite, (ii) les courbes de la répartition des revenus en
Angleterre et en Irlande présentent un parallélisme à peu près complet, (iii) les inclinaisons
des lignes mn et pq obtenues pour différents pays sont peu différentes. De ce fait, il y aurait
bien une cause qui serait à l’origine de la tendance des revenus à se disposer suivant une
certaine courbe (ici une loi). La forme de cette courbe ne dépendrait que faiblement des
conditions économiques des pays considérés (ici l’Angleterre, l’Irlande, l’Allemagne, le
Pérou…).
La surface (m n s x) représente le nombre total des revenus. La courbe (n t s) correspond à la
répartition des revenus. Il existerait ainsi un nombre de personnes représentées par la surface
(aa’bb’) ayant un revenu compris entre Oa et Oa’. Selon Pareto, on aurait coutume de parler
C
A
B
p
q
n
m
a’
a
m
b’
b
y
x s
t
n
0
c
d
0
b
a