SérieME2_TP4_Ressorts et Energétique_Enoncé

TSI1 Série 2 ME – TP4 : Ressorts et Energie Mécanique
HECKEL - 1/2
Objectif
ObjectifObjectif
Objectifs
ss
s :
::
: → Utiliser les notions d’énergies (potentielle, cinétique, mécanique)
→ Prévoir l’évolution d’un système masse + ressort
I.
I. I.
I. Le système
Le systèmeLe système
Le système :
::
: un
unun
une bille de
e bille dee bille de
e bille de f
f f
flipper
lipperlipper
lipper
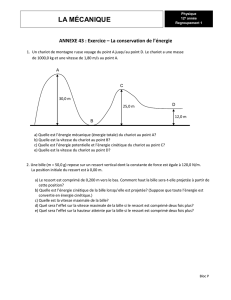
On étudie un système masse m + ressort (k, l 0 ) sur un plan incliné d’un
angle α, qui ressemble au système utilisé dans les flippers pour communiquer à
la bille son mouvement initial. On souhaite vérifier à l’aide de ce système la
conservation de l’énergie mécanique de la bille au cours du mouvement, dans le
cas où les frottements sont négligés.
Commençons par définir les 3 longueurs caractéristiques qui vont être utilisés
dans tout le problème :
- l 0 , longueur à vide : longueur du ressort lorsqu’il est tout seul, n’est
soumis à aucunes contraintes extérieures.
- l R , longueur au repos : longueur que prend le ressort lorsque la bille est
posée dessus. Elle sera légèrement inférieure à l 0 , selon la masse…
- l C , longueur comprimée : c’est la longueur prise par le ressort lorsque le
joueur tire sur la tige avant de lancer la bille.
I
II
II.
I. I.
I. Position d
Position dPosition d
Position d’
’’
’équilibre
équilibreéquilibre
équilibre –
––
– étude
étude étude
étude énergétique
énergétiqueénergétique
énergétique
La position d’équilibre peut être calculée soit avec un PFD (méthode classique
déjà réalisée), ou de manière énergétique.
I
II
II
II
I.
..
.1
11
1 Bilan des Forces
Bilan des ForcesBilan des Forces
Bilan des Forces
La bille est soumise à 3 forces :
I
II
II
II
I.
..
.2
22
2 Recherche de la position d
Recherche de la position dRecherche de la position d
Recherche de la position d’
’’
’équilibre
équilibreéquilibre
équilibre stable
stable stable
stable
On cherche le fond de la cuvette de potentiel, mais attention, il faut
additionner les deux potentiels en présence :
Questions
QuestionsQuestions
Questions :
::
:
 Tracer l’allure de l’évolution de l’énergie potentielle totale
 Calculer la position d’équilibre x eq , et en déduire la longueur l R au repos
 Vérifier votre valeur à l’aide d’un PFD.
Série 2 ME
Série 2 ME Série 2 ME
Série 2 ME –
––
– TP
TP TP
TP4
44
4 :
: :
: Ressort
RessortRessort
Ressorts
ss
s et
et et
et E
EE
Energ
nergnerg
nergie
ieie
ie M
MM
Mécanique
écaniqueécanique
écanique
x
α
l
C
l
R
g
O
Longueur au repos l
R
Longueur à vide l
0
Longueur comprimé l
C
Joueur
Pesanteur
l
0
Réaction du support
Réaction du supportRéaction du support
Réaction du support
= +
N T
R R R
NON conservative
 PAS d’E P
Poids
PoidsPoids
Poids
=
P m g
CONSERVATIF
= +
PES
P
E mgz C
Tension
Tension Tension
Tension du
du du
du ressort
ressortressort
ressort
(
)
= − −
0
x
T k l l e
CONSERVATIF
( )
= − +
2
0
1
'
2
ELAST
P
E k l l C
( )
⇒= + − +
2
0
1
''
2
TOTALE
P
E mgz k l l C
(
)
α
=sin
PES
P
E mg x
x
=
2
1
2
ELAST
P
E k x
x
On impose l’origine x = 0 pour l = l 0
x
TOTALE
P
E

TSI1 Série 2 ME – TP4 : Ressorts et Energie Mécanique
HECKEL - 2/2
I
II
II
II
II
II
I.
. .
. Etude dynamique
Etude dynamiqueEtude dynamique
Etude dynamique –
––
– Energie mécanique
Energie mécaniqueEnergie mécanique
Energie mécanique
I
II
II
II
II
II
I.
..
.1
11
1 Bilan d
Bilan dBilan d
Bilan d’
’’
’éner
éneréner
énergie
giegie
gie
Au cours du mouvement, on repère trois positions caractéristiques :
- A : Bille immobile, ressort comprimé avant lâché
- B : Bille animé de sa vitesse v 0 maximale au moment où elle quitte le ressort
- C : Bille au sommet de sa trajectoire, la vitesse s’annule
On souhaite exprimer l’énergie mécanique de la bille en chacun de ces points.
Si on suppose qu’il n’y a pas de frottements, alors E m (A) = E m (B) = E m (C)
Questions
QuestionsQuestions
Questions théoriques
théoriques théoriques
théoriques :
::
:
 Simplifier les expressions de E m (A) = E m (B) = E m (C)
 En déduire l’expression de la longueur L parcourue par la bille en
fonction de l’élongation δl que le joueur impose sur le ressort, de k,
de m, de g et de l’angle α.
 En déduire également l’expression de v 0 en fonction de H, puis de L. Quel
résultat classique retrouve-t-on ?
I
II
II
II
II
II
I.
..
.2
22
2 Mesures
MesuresMesures
Mesures
Paramètre
ParamètreParamètre
Paramètre s
ss
s :
::
:
 Mesurer l’angle α (on mesurera l’angle opposé et l’hypoténuse…)
 Mesurer la masse de la bille
 Beaucoup d’approximations sont faites ici pour simplifier les calculs. En
effet, on néglige les frottements solides (sur le plan, du ressort, …), les
frottements fluides (rondelle, ressort, bille) ainsi que la masse du ressort et
de la barre. Pour compenser un peu toutes ces approximations, on doit
prendre une valeur de la raideur du ressort réajustée. Prenons k ≈ 40 N/m
Manipulation
ManipulationManipulation
Manipulations
ss
s :
::
:
 Remplir le tableau suivant des longueurs L en fonction de δl
δl 2 cm 2,5 cm 3 cm 3,5 cm 4 cm
L
 Mesurer pour certaines élongations la valeur de la vitesse initiale v 0 . On
utilisera pour cela la webcam et le logiciel Generis déjà étudié. (la
mesure étant assez longue, on ne la fera que pour un ou deux cas…)
Comparaison
Comparaison Comparaison
Comparaison avec la
avec laavec la
avec la théorie
théorie théorie
théorie :
::
:
 Relation entre L et la vitesse initiale v 0 :
- A l’aide de la partie III.1, déduire de chacune de vos valeurs de L la
vitesse v 0 que l’on s’attend à trouver.
- Comparer avec les mesures et commenter.
- La fameuse relation
=
2
v gh
est-elle vérifiée ?
 Relation entre δl et L :
- Toujours à l’aide de la partie III.1, calculer pour chacun des cas
mesurés la longueur L à laquelle on devait s’attendre en fonction
de la quantité tirée par le joueur δl.
- Comparer avec les mesures et commenter.
x
α
l
C
l
0
≈
l
R
g
O
A
B
C
0
v
L
H