DM8 + correction

3A Devoir maison n°8
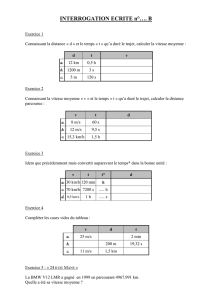
Sur une plage, un maître nageur sauveteur M aperçoit une personne B qui semble en difficulté en mer.
Il envisage immédiatement deux trajets possibles pour aller la secourir.
: Trajet 1 (ligne droite) : Trajet 2
Quel est le trajet qui lui permet d’arriver le plus rapidement auprès du baigneur ? Justifie ta réponse.
Informations :
 MC = 20 m ; CD = 15 m et CF = 44 m.
 D  [MB] et C  [MF].
 Sur la plage le maître nageur court à une vitesse de 5 m/s.
 Avec ses palmes, il nage à la vitesse de 2,5 m/s.
 Il lui faut 5 secondes pour mettre ses palmes.
3A Devoir maison n°8
Sur une plage, un maître nageur sauveteur M aperçoit une personne B qui semble en difficulté en mer.
Il envisage immédiatement deux trajets possibles pour aller la secourir.
: Trajet 1 (ligne droite) : Trajet 2
Quel est le trajet qui lui permet d’arriver le plus rapidement auprès du baigneur ? Justifie ta réponse.
Informations :
 MC = 20 m ; CD = 15 m et CF = 44 m.
 D  [MB] et C  [MF].
 Sur la plage le maître nageur court à une vitesse de 5 m/s.
 Avec ses palmes, il nage à la vitesse de 2,5 m/s.
 Il lui faut 5 secondes pour mettre ses palmes.

Corrigé.
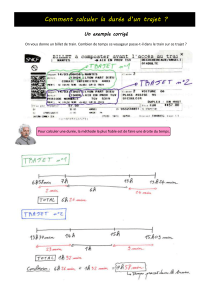
Trajet 1 :
Le triangle MDC est rectangle en C. D’après le théorème de Pythagore, on a :
MD2 = MC2 + CD2
MD2 = 202 + 152
MD2 = 400 + 225
MD2 = 625
MD = 
MD = 25 m
Il court sur une distance de 25 mètres à la vitesse de 5 m/s, soit pendant 
 = 5 secondes.
D’une part les points M, D, B et d’autre part les points M, C, F sont alignés.
Les droites (DC) et (BF) sont perpendiculaires à la droite (CF), donc elles sont parallèles entre elles.
D’après le théorème de Thalès, on a :
 avec MF = MC + CF = 20 + 44 = 64 m
Soit 
 donc MB =    80 m et DB = MB – MD = 80 – 25 = 55 m
Il nage 55 mètres à la vitesse de 2,5 m/s, soit pendant 
  12 secondes.
Durée totale pour le trajet 1 :
5 + 5 + 22 = 32 secondes
Trajet 2 :
 donc BF =    48 m
Le quadrilatère CFBG a trois angles droits, c’est donc un rectangle ainsi CG = BF = 48 m
Et GB = CF = 44 m.
Il nage 44 mètres à la vitesse de 2,5 m/s, c’est-à-dire pendant 
  17,6 secondes.
Le triangle MCG est rectangle en C. D’après le théorème de Pythagore, on a :
MG2 = MC2 + CG2
MG2 = 202 + 482
MG2 = 400 + 2304
MG2 = 2704
MG = 
MG = 52 m
Il court sur une distance de 52 mètres à la vitesse de 5 m/s, soit pendant 
 = 10,4 secondes.
Durée totale pour le trajet 2 :
17,6 + 5 + 10,4 = 33 secondes