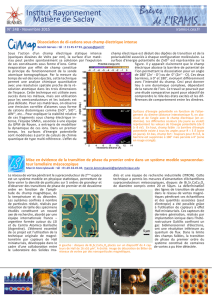
Transitions de phase dans l`état mixte des supraconducteurs de type II

La propriété la plus spectacu-
laire des matériaux supracon-
ducteurs est probablement le
fait qu'ils présentent une résistance
électrique parfaitement nulle en des-
sous d’une température critique Tc.
Mais ces matériaux ont également la
remarquable capacité de pouvoir
expulser un champ magnétique exté-
rieur H(effet Meissner). Cette
expulsion s’explique par l’apparition
de courants supraconducteurs de
densité jM~H/λ circulant à la péri-
phérie de l’échantillon sur une pro-
fondeur λde l’ordre de quelques
milliers d’Angström. Ces courants
créent une aimantation M=−Hqui
permet d’annuler l’induction magné-
tique Bà l’intérieur du supraconduc-
teur (B=µ0(H+M)=0).jMne
peut toutefois pas dépasser une
valeur maximale j0et, dans les
supraconducteurs dits de type I, la
supraconductivité est alors brutale-
ment détruite au-dessus du champ
Hcpour lequel jM=j0(appelé
champ critique thermodynamique).
En revanche, dans les supraconduc-
teurs dits de type II, il devient éner-
giquement favorable de « laisser
pénétrer » partiellement B au-dessus
d’un seuil Hc1. Le champ pénètre
alors sous la forme de tubes de flux
appelés vortex portant chacun un
quantum de flux 0=h/2e(créé
par un « tourbillon » de courant de
densité jV). Afin de permettre le pas-
sage du champ magnétique, la supra-
conductivité est détruite dans le
cœur du vortex sur une distance ξde
l’ordre de 10 à 50 Å et jVs’éteint
progressivement sur une distance λ
(figure 1). On a alors coexistence des
phases supraconductrice et normale
(i.e. non supraconductrice) dans
l’échantillon ; cet état intermédiaire
a donc été appelé état mixte. Le flux
porté par chaque ligne étant quanti-
fié, l’augmentation de l’induction
magnétique dans l’échantillon
lorsque le champ extérieur croît ne
peut se faire qu’en augmentant la
densité de vortex. La phase supra-
conductrice est finalement détruite
au-dessus du champ critique supé-
rieur Hc2pour lequel les cœurs des
vortex se recouvrent et occupent tout
l’échantillon.
La présence de vortex dans l’état
mixte a des conséquences essen-
tielles sur les propriétés physiques du
matériau. Par exemple, la réponse
électrodynamique du supraconduc-
teur est presque entièrement détermi-
née par leur comportement. En effet,
lorsque l’on applique un courant de
densité j, les vortex sont soumis à
une force de Lorentz FL=j×Bqui
peut les mettre en mouvement à une
vitesse vproduisant ainsi un champ
électrique E=v×B. Le déplace-
ment des électrons « normaux » pré-
sents dans les cœurs de vortex est
alors à l’origine d’une résistivité
ρf=vB/jet le supraconducteur
n’est donc plus en mesure de condui-
re un courant électrique sans perte :
sa principale propriété est perdue.
Toutefois, tous les échantillons
contiennent des défauts topologiques
(interstices, lacunes, dislocations),
chimiques ou « géométriques »
(rayures, cassures) qui constituent
d’excellents centres de piégeage des
vortex. Ceux-ci restent alors ancrés
sur ces défauts et le champ électrique
E=v×Breste nul pour des densi-
tés de courant jinférieures à une
valeur « critique » jc.
Pour décrire la répartition des
vortex dans le supraconducteur,
71
Transitions de phase
Transitions de phase dans l’état
mixte des supraconducteurs
de type II
Dans les supraconducteurs dits de type II, le champ magnétique peut pénétrer sous la forme de
tubes de flux quantifiés appelés vortex. Dans les oxydes supraconducteurs, mais également dans
certains composés intermétalliques ou organiques, l’organisation spatiale de ces vortex peut
adopter, selon le champ magnétique ou la température, des structures très variées : réseau ordon-
né, verres, phase liquide... La diffraction de neutrons et la magnéto-optique sont alors des outils
performants qui permettent d’étudier les transitions de phase entre ces différentes structures.
– Laboratoire d’études des propriétés élec-
troniques des solides (LEPES) UPR 11
CNRS, 25 av. des martyrs, BP 166, 38042
Grenoble cedex 9.
– Laboratoire des solides irradiés (SESI),
UMR 7642 CNRS, CEA, École polytech-
nique, route de Saclay, 92128 Palaiseau
cedex.
ns(x)
B(x
)
j
V
(x)
ξλ
x
j
V
B
Figure 1 - A gauche, représentation schématique
d’un vortex. A droite, profils de la densité de
paires de Cooper nSde l’induction B, et du cou-
rant non dissipatif jV(x est la coordonnée
radiale).

défauts présents dans l’échantillon
altèrent cette distribution « idéale »,
puisque chaque vortex cherche alors
une position qui lui permet de mini-
miser la somme des énergies d’an-
crage et d’interaction entre vortex.
Cependant, l’observation de dizaines
de milliers de vortex parfaitement
ordonnés (sans aucune dislocation)
dans des supraconducteurs comme
Bi2Sr2CaCu2O8a montré que le soli-
de de vortex pouvait conserver un
ordre hexagonal à longue distance
quasi parfait. Le solide de vortex pré-
sente toujours des pics de Bragg en
diffraction mais, comme dans un
verre, sa fonction de corrélation posi-
tion – position tend vers zéro à (très)
grande distance. T. Giamarchi et P. Le
Doussal l’ont donc baptisé « verre de
Bragg ».
Toutefois, le verre de Bragg
n’existe que dans des conditions
72
ceux-ci sont assimilés à des lignes
de flux élastiques qui obéissent à
une électrodynamique classique
(modèle de London). Comme
chaque vortex est entouré d’un tour-
billon de courant (jV)de même
signe, les tubes se repoussent et, en
l’absence de désordre statique (i.e.
de défauts) ou thermique, ils se
répartiraient dans l’échantillon sous
la forme d’un réseau hexagonal
appelé réseau d’Abrikosov. Les
Encadré 1
DIAGRAMME DE PHASES H-T
DES SUPRACONDUCTEURS DE TYPE II
Le diagramme de phases champ magnétique – température
des supraconducteurs de type II déduit de la théorie de
Ginzburg et Landau (en ignorant les fluctuations thermiques
et l’ancrage des vortex par les défauts) est présenté schémati-
quement en figure (a) (l’insert illustre l’ordre hexagonal du
réseau d’Abrikosov). Toutefois, comme les échantillons réels
contiennent tous des défauts, on s’attend à ce que le réseau
d’Abrikosov soit remplacé par une nouvelle structure appelée
« verre de Bragg », qui conserve néanmoins un ordre à longue
distance « quasi parfait ». De plus, dans les supraconducteurs
à haute Tc, de fortes fluctuations thermiques peuvent condui-
re à la fusion du solide de vortex vers une phase liquide et le
diagramme de phases serait alors celui de la figure (b).
Notons que, dans la phase liquide, les lignes de flux peuvent
aisément « se couper » et se reconnecter. L’ancrage de ces
lignes devient alors impossible et la phase liquide présente
une forte résistivité : cette ligne de fusion correspond donc à
une frontière importante au-delà de laquelle le principal
attrait de la supraconductivité est perdu. Pour un taux de
défauts plus important, l’ordre orientationnel et translationnel
est également détruit dans la phase solide. Il a alors été sug-
géré qu’une transition entre le verre de Bragg et un verre de
vortex totalement désordonné pourrait être induite à basse
température par le champ magnétique [figure (c)].
Finalement, on s’attend à ce que le verre de Bragg disparais-
se pour un taux de désordre très important [figure (d)].
L’existence d’une transition entre le verre de Bragg et un
liquide de vortex à haute température a été mise en évidence
dans les oxydes supraconducteurs dès 1992, car elle se traduit
par exemple par un saut brutal de la résistance électrique à
zéro. En revanche, le verre de vortex et le liquide sont tous
deux totalement désordonnés et la différence entre ces deux
phases n’est plus topologique mais dynamique. Le passage
entre le verre de vortex et le liquide est donc beaucoup plus
continu (il n’y a pas de saut de résistance) et l’existence d’une
véritable transition thermodynamique entre ces deux struc-
tures reste encore très controversée. L’étude expérimentale de
la transition basse température entre le verre de Bragg et une
phase désordonnée [liquide : figure (b) ou verre de vortex :
figure (c)] est beaucoup plus délicate. Nous avons montré que
la diffraction de neutrons et l’imagerie magnéto-optique sont
des outils très performants pour cette étude (voir le texte prin-
cipal). Notons que les échantillons de très bonne qualité
comme Bi2Sr2CaCuO8+δappartiennent sans doute au cas
(b), alors que le diagramme de phases des systèmes plus
désordonnés comme (K,Ba)BiO3est plus proche du cas (c).

réduites de champ et de température
(encadré 1) et l’on s’attend à observer
une transition de phase dans l’état
mixte entre cette phase ordonnée à
bas champ et basse température et
une phase totalement désordonnée
constituée de lignes de flux enchevê-
trées au-dessus d’une ligne He(T). A
haute température (T>Tc/2), cette
transition est tout à fait similaire à la
fusion des réseaux cristallins. Les
vortex sont libres de se déplacer dans
la phase liquide qui présente alors
une forte résistance électrique ; c’est
l’observation d’un saut de résistance
qui a suggéré, dès 1992, l’existence
de cette fusion, et des mesures de
chaleur spécifique et d’aimantation
ont confirmé en 1996 qu’il s’agit bien
d’une transition de phase thermody-
namique du premier ordre.
A plus basse température, la situa-
tion se complique car l’ancrage
devient si fort qu’il est alors impos-
sible d’obtenir la distribution des vor-
tex à l’équilibre, et donc de mesurer
des quantités thermodynamiques.
Bien que l’existence d’une transition
de phase ait été suggérée par simula-
tion numérique et à partir de mesures
magnétiques, des preuves définitives
de son existence restaient délicates à
obtenir. Un ancrage important donne
lieu à une résistance électrique nulle
(ou inférieure aux limites de résolu-
tion expérimentales) dans les deux
phases, et les mesures de transport
électrique ne sont, par exemple, plus
une sonde adaptée. Nous verrons dans
la suite de cet article que la transition
ordre - désordre peut alors être étudiée
à partir i) de mesures de diffraction de
neutrons et ii) de mesures magnéto-
optiques.
Il est remarquable de noter que
des supraconducteurs très différents
montrent tous le même diagramme de
phases phénoménologique (lorsqu’ils
sont synthétisés sous forme suffisam-
ment pure). Les échelles de champ et
de température sont néanmoins très
différentes. Par exemple, le champ
Hepeut être supérieur aux valeurs
expérimentalement accessibles dans
des monocristaux d’YBa2Cu3O7−δet
n’est que de quelques centièmes de
Tesla dans Bi2Sr2CaCu2O8+δ(la très
forte anisotropie électronique de ce
composé réduit considérablement la
rigidité des lignes de flux). Le cas de
Bi2Sr2CaCu2O8+δest si extrême
qu’il avait initialement été suggéré
que la disparition du réseau de vor-
tex observée par diffraction de neu-
trons était particulière à ce seul com-
posé, et était liée au découplage des
plans supraconducteurs. Pour pou-
voir confirmer l’existence et la géné-
ralité d’une transition ordre – désor-
dre induite à basse température par
le champ magnétique, il était donc
nécessaire d’étudier un système iso-
trope, pour lequel les effets dimen-
sionnels ne rentreraient pas en ligne
de compte. Pour cela, nous nous
sommes intéressés au système
(K,Ba)BiO3(Tc≈30 K), qui présen-
te une structure cristallographique
cubique de type Perovskite parfaite-
ment tridimensionnelle (les trois
axes cristallographiques principaux
sont équivalents) et pour lequel nos
mesures de diffraction de neutrons
ont permis de confirmer l’existence
de cette transition
Il restait alors à comprendre com-
ment le solide de vortex « passe »
d’une phase à l’autre lorsque l’on
augmente le champ magnétique
extérieur. Pour cela, l’imagerie
magnéto-optique se révèle être un
outil très performant. En effet, cette
technique permet d’effectuer une
cartographie du champ magnéti-
que dans l’échantillon et de « visua-
liser » ainsi la distribution spatiale
des différentes structures (phases !)
de vortex. Pour ces mesures, nous
avons utilisé des monocristaux de
Bi2Sr2CaCu2O8+δ, composé pour
lequel le champ de transition est suf-
fisamment faible (la résolution de
cette technique est limitée à
quelques centaines de Gauss) ; nous
verrons ainsi que les deux phases
peuvent coexister dans l’échantillon
sous certaines conditions de champ
et de température. Elles sont alors
séparées par une interface abrupte
qui se déplace progressivement jus-
qu’à destruction totale d’une des
deux phases (la phase ordonnée dis-
paraît au-dessus de Heet, inverse-
ment, la phase désordonnée n’existe
que de façon métastable au-dessous
de He).
TRANSITION ORDRE – DÉSORDRE :
DIFFRACTION DE NEUTRONS
La structure du réseau de vortex,
tout comme leur comportement
dynamique, sont étroitement liés à la
nature du désordre présent dans le
matériau : densité, taille et type de
défauts. Dans le cas d’une réparti-
tion aléatoire de défauts ponctuels
(de taille inférieure à la taille du
cœur du vortex ξ), les vortex sont
amenés à « errer » dans le potentiel
aléatoire créé par ces défauts à la
recherche des endroits où le gain en
énergie de piégeage est maximal.
Cette recherche nécessite toutefois
des déformations élastiques, soit de
l’ensemble du réseau de vortex, soit
de chacune des lignes de flux indivi-
duellement lorsque leur densité est
faible. Ces déformations ont un coût
énergétique et la structure du solide
de vortex résulte alors d’un compro-
mis subtil entre le gain en énergie de
piégeage par les défauts (Ep)et le
coût énergétique associé aux défor-
mations élastiques (Eél).
Les progrès en cristallogenèse
des supraconducteurs à haute tem-
pérature critique ont permis d’éla-
borer des échantillons d’une qualité
telle, qu’à faible champ, le gain en
énergie Epassocié à des déforma-
tions importantes (i.e. de l’ordre du
pas du réseau a0) soit très large-
ment inférieur à Eél: le verre de
Bragg est alors la structure d’équi-
libre du solide de vortex. On peut
montrer que Epet Eéldécroissent
tous deux avec le champ extérieur.
Toutefois, cette décroissance est
plus rapide pour Eélet des déplace-
ments de l’ordre de a0entre vortex
voisins peuvent devenir énergique-
ment favorables au-dessus d’un
champ seuil He(T)pour lequel Ep
devient supérieur à Eél. Des dislo-
cations prolifèrent alors dans le
réseau de vortex, détruisant ainsi
l’ordre à longue distance, pour lais-
73
Transitions de phase

pérature nous a permis de montrer
que ce solide est bien le verre de
Bragg proposé par T. Giamarchi et
P. Le Doussal.
Dans le modèle de London, l’in-
tensité totale (I) intégrée dans le plan
du détecteur et sur l’ensemble des
angles θest proportionnelle à
2π/q.F2(q)où F(q)est un facteur
de forme lié à la distribution du
champ magnétique dans l’échan-
tillon. Pour qλ>>1(condition
généralement vérifiée), F(q)α1/λ2
et l’on s’attend donc à ce que le pro-
duit I.q soit indépendant du champ
magnétique (en tenant compte de la
taille finie des cœurs des vortex, on
peut montrer que I.q tend en fait pro-
gressivement vers zéro pour
H=Hc2). Toutefois, comme le
montre la figure 2, dans (K,Ba)BiO3
tout comme dans Bi2Sr2CaCu2O8+δ
ce produit chute rapidement avec le
champ magnétique et s’annule au-
dessus d’un champ Hetrès inférieur à
Hc2 :∼1 à 2 T dans (K,Ba)BiO3
(Bc2(0)∼30T)et de quelques cen-
tièmes de Tesla dans Bi2Sr2CaCu2
O8+δ(Bc2(0)∼80T). Dans Bi2Sr2
CaCu2O8+δ, le premier composé
dans lequel cette « disparition anor-
male » de l’intensité avait été obser-
vée, elle avait été attribuée par
R. Cubitt et ses collaborateurs à un
découplage des plans supraconduc-
teurs. Cette hypothèse est incompa-
tible avec la structure cubique de
(K,Ba)BiO3dont l’étude présente
ici tout son intérêt. La disparition de
toute intensité diffractée au-dessus
de Heest donc probablement liée à
l’apparition de dislocations dans la
phase désordonnée et ces mesures
ont ainsi permis de valider l’hypo-
thèse d’une transition ordre –
désordre induite à basse température
par le champ magnétique aussi bien
dans (K,Ba)BiO3que dans
Bi2Sr2CaCu2O8+δ.
DISTRIBUTION SPATIALE DES DIFFÉRENTES
STRUCTURES DE VORTEX
On peut s’attendre à ce que la pro-
lifération de dislocations lors de la
transition ordre – désordre s’accom-
pagne d’une forte augmentation du
piégeage et donc d’un accroissement
de la densité de courant « critique »
pouvant être induite dans le maté-
riau. Les densités de courants en jeu
sont trop fortes pour être mesurées à
partir de mesures de transport clas-
siques, mais peuvent l’être à partir
de mesures magnétiques. En effet, le
piégeage des vortex donne lieu à une
hystérésis dans la relation M-H qui
fut décrite pour la première fois par
C. Bean dans les années 60 (enca-
dré 2). L’ouverture du cycle d’hysté-
résis est directement proportionnelle
au courant jinduit par la variation
de champ. On sait depuis fort
longtemps que, dans de nombreux
supraconducteurs (Nb, NbZr,
74
ser place à un ensemble de lignes
enchevêtrées dans la phase désor-
donnée (encadré 1).
Porteurs d’un moment magné-
tique, les neutrons sont sensibles au
champ magnétique présent dans le
cœur du vortex et sondent donc la
structure magnétique créée par le
solide de vortex. Tout comme pour
la diffraction de rayons X par un
réseau cristallin, un faisceau de neu-
trons (de longueur d’onde λN~ 10 à
20 Å) est diffracté par un système
ordonné de vortex lorsque la condi-
tion de Bragg : qλN=2πsin(θ) est
satisfaite (qest le vecteur du réseau
réciproque associé au réseau de vor-
tex et θl’angle entre le champ
magnétique et le faisceau). En fai-
sant « pivoter » le champ (i.e. le soli-
de de vortex) autour du faisceau de
neutrons, on obtient alors une figure
de diffraction analogue à un cliché
de diffraction de rayons X par un
cristal atomique qui reflète la symé-
trie du (quasi-)réseau de vortex. Un
cliché de diffraction obtenu à 2.5 K
dans un monocristal (K,Ba)BiO3
(pour un champ extérieur de 0.1 T)
est présenté dans l’insert de la figure
2 ; il montre que le solide est parfai-
tement ordonné à bas champ et basse
température. Une analyse détaillée
de l’évolution de la dépendance
angulaire de l’intensité diffractée
avec le champ magnétique et la tem-
0
0.2
0.4
0.6
0.8
1
1.2
0 0.2 0.4 0.6 0.8 1
I.q(H)/I.q(0)
H/H
e
Figure 2 - Évolution de l’intensité intégrée sous
le pic de diffraction (1,0) du réseau de vortex
(verre de Bragg) en fonction du champ magné-
tique appliqué T=2.5K)dans (Ba,K)BiO3
(triangles) et Bi2Sr2CaCuO8(carrés). Insert :
cliché de diffraction d’un faisceau de neutrons
par le réseau de vortex dans (Ba,K)BiO3(H =
1000G, T = 2.5 K.
-1
0
1
01 234 56
M (a.u.)
µ0H (T)
4K
phase
désordonnée
verre
de Bragg
He
(a)
Hp
-200
-100
0
100
200
-0.2 -0.1 0 0.1 0.2
Bz/µ0-Ha (Oe)
µ0H (T)
Hp
(b)
Figure 3 - (a) Demi-cycle d’aimantation (H > 0) mesuré dans un échantillon de (K,Ba)BiO3par un
magnétomètre supraconducteur (SQUID). Le champ Hede transition ordre – désordre déduit des mesures
de diffraction de neutrons (figure 2) est très proche du second pic Hp. (b) Cycle d’hystérésis magnétique
mesuré à l’aide d’une sonde de Hall microscopique disposée sur la surface d’un monocristal de
Bi2Sr2CaCu2O8+δ(T = 24.2 K). On voit clairement l’accroissement de l’amplitude du cycle (i.e. du
courant) au-dessus de µ0Ha~ 0.04T.

α−Nb3Ge,…), ce courant présente
un « effet de pic » à l’approche du
champ critique supérieur Hc2. De
même, presque tous les oxydes à
haute Tcprésentent une dépendance
non monotone du courant en fonc-
tion du champ extérieur (figure 3).
Toutefois, la particularité des oxydes
est que le champ Hpcorrespondant
au maximum de courant (second
pic) est très nettement inférieur à
Hc2. De nombreuses hypothèses ont
été proposées pour expliquer cet
effet (défauts de stœchiométrie en
oxygène, transition 2D-3D du réseau
de vortex...). Nous avons montré
que, dans nos échantillons de
(K,Ba)BiO3,Hpest très proche du
champ Hedéterminé par diffraction
de neutrons, ce qui suggère que l’ac-
croissement du courant est effective-
ment lié à la transition ordre –
désordre (figure 3a). Cette interpré-
tation est corroborée par le fait que
l’introduction d’un grand nombre de
défauts ponctuels dans l’échantillon
conduit à une diminution de Hp(la
75
Transitions de phase
Encadré 2
ÉCRANTAGE DU FLUX
DANS LES SUPRACONDUCTEURS DE TYPE II
Dans les supraconducteurs de type II, l’écrantage du champ
magnétique extérieur H n’est total (i.e. B = 0) que pour
H<Hc1. Au-delà de cette valeur, H pénètre dans l’échan-
tillon sous la forme de tubes de flux quantifiés appelés vortex.
En l’absence d’ancrage, ces vortex adopteraient une réparti-
tion spatiale quasi homogène et l’évolution du moment
magnétique B–µ0H(moyenné sur un grand nombre de vor-
tex) en fonction du champ extérieur H serait décrite par la
courbe grisée en figure a.
Les vortex sont créés sur les bords de l’échantillon puis se
déplacent vers le centre. La présence de défauts entrave ce
déplacement et conduit à une distribution très inhomogène des
lignes de flux qui restent piégées près des bords : leur concen-
tration (donc l’induction B) est plus forte à la périphérie de
l’échantillon qu’elle ne l’est au centre. Cette distribution
inhomogène du flux donne lieu à une densité de courant j(x)
reliée au gradient local du champ et, pour prédire les distri-
butions de B(x) et j(x), il faut résoudre les équations de
Maxwell en y injectant la relation E(j) qui caractérise la
« force du piégeage ».
B étant inhomogène, une mesure locale (obtenue en plaçant
une micro-sonde à effet Hall sur la surface de l’échantillon)
dépendra de la position x. La courbe M(H) obtenue au centre
de l’échantillon est présentée en figure a (cycle noir). Les
flèches indiquent le sens dans lequel le cycle est parcouru et
les profils de champ correspondants aux points 1 à 4 sont pré-
sentés en figure b (l’échantillon est compris entre x=– l/2 et
x = +l/2). Lorsque le champ extérieur décroît, j change de
signe et les vortex sortent de l’échantillon : B diminue
d’abord près des bords (point 3) puis progressivement à l’inté-
rieur de l’échantillon. Les profils de B (et donc la valeur de
M) obtenus pour la même valeur du champ extérieur en
champ croissant puis décroissant – points 2 et 3 par exemple –
sont donc très différents ; le cycle M(H) est fortement irréver-
sible. La largeur du cycle d’hystérésis est alors directement
proportionnelle au courant j induit dans l’échantillon lors de
la rampe en champ. La particularité des supraconducteurs à
haute Tcest que j présente un maximum pour une valeur du
champ extérieur H très inférieure à Hc2(figure 3 du texte
principal). Notons que sur la branche descendante du cycle
B(x) est supérieur au champ extérieur µ0Het qu’un flux
rémanent restera piégé dans l’échantillon pour Ha=0
(point 4).
H
µ0M = B-µ
0
H
1
2
3
4
j - l
H
c2
Figure a
-l/2 0 l/2
µ0H1
x x
µ0H2
-l/2 0 l/2
µ0H3
=
µ0H2
x
-l/2 0 l/2
µ0Hc1
x
µ0H4=0
-l/2 0 l/2
B
BB
B
Figure b