CONVERSION DE PUISSANCE

Spé ψ 2001-2002 page 1/6 Devoir n°6
Spé ψ 2001-2002 Devoir n°6
CONVERSION DE PUISSANCE
Les trois parties sont indépendantes.
PARTIE I
DETERMINATION DES CARACTERISTIQUES D’UN MOTEUR
On considère un moteur à courant continu, bipolaire, à excitation indépendante, par-
faitement compensé. Ce moteur pouvant être relié ou non à un dispositif type frein poudre.
La plaque signalétique du moteur indique :
puissance nominale : 0,80 kW ; vitesse nominale : 1500 tr/min
tension nominale d'alimentation : 220 V ; intensité nominale d'induit : 4,6 A
intensité nominale dans l'inducteur : 0,35 A
I-1) L'induit du moteur en rotation peut être modélisé par le di-
pôle ci-contre, E est la force contre-électromotrice (f.c.é.m.). Justifier
rapidement la relation E = Φ0Ω où Ω est la vitesse de rotation en rad/s,
que représente Φ0 ?
I-2) Détermination des résistances des circuits inducteurs RE et induit RI.
a) Une mesure rapide, avec un ohmmètre, de la résistance de l'inducteur donne une
valeur affichée de 512 Ω avec une précision de 0,5% (de la valeur lue) ± 1 digit. Donner l'in-
tervalle où se situe la valeur RE.
b) On veut maintenant mesurer la résistance RI du circuit induit. Pour les conditions
expérimentales, répondre aux questions ou choisir, en justifiant ce choix, parmi les proposi-
tions suivantes :
La mesure s'effectue rotor bloqué ou tournant à vitesse réduite ?
Pourquoi laisse-t-on tourner le moteur à sa vitesse nominale avant la mesure ?
Peut-on utiliser un ohmmètre ?
La mesure a été effectuée par la méthode voltampèremétrique, on a relevé les valeurs suivan-
tes pour lesquelles U est la tension mesurée par un voltmètre numérique d'impédance d'entrée
élevée (10 MΩ) et II l'intensité du courant dans l'induit :
U (en V) 2,31 4,61 6,90 9,20 11,5 13,8
II (en A) 0,50 1,0 1,5 2,0 2,5 3,0
Déterminer la valeur de la résistance RI. Représenter le schéma du montage expéri-
mental pour ces mesures en justifiant les positions du voltmètre et de l'ampèremètre.
I-3) On prendra pour RI la valeur 4,6 Ω. On mesure grâce à une génératrice tachymé-
trique placée en bout d'arbre, la fréquence de rotation n du moteur en tour/minute.
a) On détermine pour deux valeurs du courant d'excitation IE dans l'inducteur les va-
leurs de E et n.
IE = 0,35 A
E (en V) 240 220 200 150 120 75 20 0
n (en tr/min) 1670 1510 1380 1035 820 510 110 0
E
R
I
U
I
I

Spé ψ 2001-2002 page 2/6 Devoir n°6
IE = 0,20 A
E (en V) 186 150 120 90 60 30 0
n (en tr/min) 1800 1450 1150 850 560 260 0
al) Indiquer un mode opératoire permettant de déterminer E.
a2) Tracer sur le même graphe E en fonction de n pour les deux valeurs de IE :
échelle 1 cm ↔ 200 tr/min et 1 cm ↔ 20 V.
a3) Justifier brièvement l'allure des courbes obtenues.
a4) Montrer que le flux Φ0 n'est pas proportionnel à l'intensité IE du courant
dans l’inducteur.
b) On relève les valeurs de E et de l'intensité IE du courant dans l'inducteur pour une
fréquence de rotation maintenue constante, n = 1500 tr/min :
E (en V) 219 210 204 198 194 188 179 168 158
IE (A) 0,39 0,35 0,33 0,31 0,30 0,28 0,26 0,24 0,22
E (en V) 147 137 130 107 100 87 78 65 56
IE (A) 0,20 0,18 0,17 0,14 0,13 0,11 0,10 0,08 0,07
La courbe E(IE) est donnée ci-dessous :
Justifier, en quelques lignes, l'allure de
cette courbe.
I-4) On note :
Ÿ PA : la puissance électrique absorbée
totale (induit et inducteur),
Ÿ PTR : la puissance électrique transmise
au rotor,
Ÿ PU : la puissance mécanique disponible
sur l'arbre,
Ÿ PJE, PJI : les pertes par effet Joule res-
pectivement dans l'inducteur et dans l'induit,
Ÿ PC : les pertes autres que par effet Joule.
a) Avec les notations ci-dessus, représen-
ter le bilan de puissance du moteur à courant
continu à excitation indépendante.
b) Le terme PC regroupe les pertes méca-
niques PM et les pertes fer PF : expliciter briève-
ment ces termes, de quels paramètres dépendent-
ils ? c) Un modèle équivalent de l'induit a été
donné au 1), proposer un modèle de l'inducteur quand le moteur est en régime établi et en
déduire les expressions de PA, PJE, PJI.
I-5) Essai à vide à vitesse constante n = 1500 tr/min.

Spé ψ 2001-2002 page 3/6 Devoir n°6
a) Pour les conditions expérimentales, répondre aux questions suivantes, en justifiant
votre réponse :
On met sous tension l'inducteur avant l'induit ou l'inverse ?
On commence avec U = 0 et on augmente progressivement ou bien on démarre sous U
nominale ?
Lors de l'essai, comment obtient-on une vitesse constante égale à la vitesse nominale
alors que U varie et reste inférieure à U nominale ?
b) Montrer que l'on peut obtenir, pour chaque valeur de IE dans l'inducteur, grâce au
bilan de puissance, la valeur de PC en mesurant la tension U aux bornes de l'induit et l'inten-
sité II du courant dans l'induit.
c) On relève les valeurs suivantes :
U (en V) 222 213 198 176 151 120 85
II (en A) 0,43 0,44 0,45 0,48 0,56 0,66 0,92
IE (en A) 0,40 0,35 0,30 0,25 0,20 0,15 0,10
Tracer PC en fonction de IE : échelle 1 cm ↔ 0,1 A et 1 cm ↔ 10 W.
d) Déduire de la courbe précédente la valeur des pertes mécaniques PM à 1500 tr/min.
I-6) Le moteur est maintenant utilisé pour entraîner un frein à poudre qui exerce sur
l'arbre un couple résistant dont le moment MR est réglable.
a) Le point de fonctionnement est :
Ÿ n0 = 1500 tr/min,
Ÿ tension aux bornes de l'induit U0 = 212 V,
Ÿ intensité du courant dans l'induit II0 = 3,0 A.
al) Calculer la f.c.é.m. E dans l'induit et en déduire la valeur de IE0 intensité du
courant dans l'inducteur.
a2) Calculer la puissance disponible sur l'arbre (puissance utile) PU.
a3) Calculer la valeur du couple résistant MR.
b) On maintient IE constant et égal à 0,31 A. On modifie la valeur de la tension U aux
bornes de l'induit et on ajuste MR pour que l'intensité du courant dans l'induit reste constante
et égale à II0.
bl) Montrer que le moment ME du couple électromagnétique est constant. Cal-
culer sa valeur.
b2) Exprimer la fréquence de rotation n en tr/min en fonction de U sous la
forme n = aU + b. Donner les expressions de a et b.
b3) On relève les valeurs suivantes :
U (en V) 200 100 40
n (en tr/min) 1416 666 200
Tracer n en fonction de U : échelle 1 cm ↔ 20 V et 1 cm ↔ 200 tr/min.
Pour quelle valeur de U a-t-on n = 0 ? Comparer à la valeur prévue par la relation du
I–6-b2).

Spé ψ 2001-2002 page 4/6 Devoir n°6
PARTIE II
ALIMENTATION DU MOTEUR
On alimente l'induit du moteur à excitation séparée
en le plaçant entre les points A et B dans le montage ci-
contre. Pour que le courant soit ininterrompu dans le mo-
teur, on ajoute en série une inductance. On appelle L l'in-
ductance totale du modèle électrique entre A et B et R la
résistance.
Ÿ Va : tension d'alimentation supposée cons-
tante, Va > 0, Ÿ ia : intensité instantanée du courant fourni
par l'alimentation,
Ÿ D : diode idéale : tension aux bornes nulle quand elle est passante et intensité
du courant nulle quand elle est bloquée,
K1 : interrupteur unidirectionnel idéal commandé.
La commande de K1 est périodique de période T, on choisit l'origine des temps t = 0
telle que, pour la première période étudiée :
t ∈ ]0, αT[ : K1 est fermé
t ∈ ]αT, T[ : K1 est ouvert
α : rapport cyclique est compris entre 0 et 1.
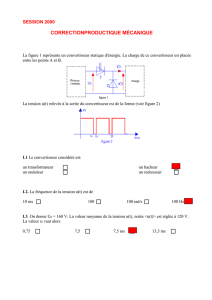
II-1) Étude de u(t)
a) En justifiant brièvement le fonctionnement, préciser les séquences de conduction de
la diode.
b) Tracer u(t) sur l'intervalle [0, T], puis exprimer U, valeur moyenne de u(t), en fonc-
tion de Va et α.
II-2) Étude de i(t).
a) Écrire l'équation différentielle liant u(t) et i(t) en supposant que la f.c.é.m. E est
constante.
b) On donne Va = 230 V ; n = 1500 tr/min ; R = 5,0 Ω ; intensité du courant d'excita-
tion de 0,3 A, soit E = 194 V.
bl) Exprimer I, valeur moyenne de i(t), en fonction de α, Va, E et R.
b2) Calculer α pour I = 0,45 A.
c) Étude de l'ondulation i’(t) = i(t) – I.
cl) Écrire l'équation différentielle liant u(t) et i’(t).
c2) Exprimer i’(t) sur les intervalles [0, αT] et
[αT, T], on posera τ =
L
R
.
c3) Montrer que si
T
τ
<<1, l'allure de i’(t) est la
suivante :
(Les positions de I’MAX et I’MIN sont arbitraires sur ce
schéma.)
t
T
α
T
i’
(
t
)
I
’
MAX
I
’
MIN
K
1
L
R
E
↑
Va
D
A
B
ia

Spé ψ 2001-2002 page 5/6 Devoir n°6
c4) Exprimer la valeur moyenne de i’(t) en fonction de I’MAX et I’MIN, en dé-
duire que I’MAX = – I’MIN et exprimer I’MAX en fonction de Va, R, α et
T
τ
.
c5) Calculer l'ondulation ∆I’ = I’MAX – I’MIN en fonction de α, Va, T et L. Pour
quelle valeur de α, ∆I’ est-elle maximale ?
c6) On donne: Va = 230 V; R = 5,0 Ω; T = 3,0 ms et I = 0,45 A.
Exprimer LMIN, valeur minimale de L, en fonction de Va, T et I pour que la conduction
soit effectivement ininterrompue en régime établi. Calculer LMIN.
En déduire la constante de temps τMIN et vérifier l'approximation faite au 2-c3).
Partie III
TRANSFORMATEUR A IMPULSION
Le transformateur étudié sert à déclencher la conduction de l’interrupteur K1 dans le
montage d'électronique de puissance, en générant le pic d’intensité nécessaire.
Le primaire et le secondaire ont chacun le même nombre de spires N. Les caractéristi-
ques de chaque enroulement, inductance propre et résistance, sont L = 2mH et r = 1,2 mΩ.
Le noyau du transformateur est en ferrite dont
on idéalisera la caractéristique d'aimantation par la
courbe donnée sur la figure 2.
φ(t) représente le flux magnétique à travers une
section droite du circuit magnétique.
Les inductances propres L ne sont définies qu'en
dehors de la zone de saturation.
On se limite ici à une étude à vide (iS = 0)
III-1) Les notations sont définies sur la figure 3.
V est une tension positive fixe et l'interrupteur k est réalisé par un transistor bipolaire.
a) A l'instant t = 0, on ferme l'interrupteur k.
Exprimer la tension uP(t) et le courant iP(t), en déduire
le flux φ(t) et la tension secondaire uS(t) en fonction de
V et des caractéristiques du transformateur. On négli-
gera pour cette étude la résistance de l'enroulement et
on considérera qu'à t = 0, iP = 0 (conditions initiales).
b) Le flux croît alors jusqu'à saturation du cir-
cuit magnétique.
Exprimer le produit (V.t
MAX) en fonction de φSAT. Le fabricant donne
V.tMAX = 400 V.µs. En déduire la valeur de tMAX pour V = 10 V et calculer la valeur de iPMAX
qui correspond à tMAX.
c) On veut prévoir ce qui se passerait si l'interrupteur k restait fermé au-delà de tMAX.
Quelle serait alors la valeur de uS ? Montrer qu'il est nécessaire de tenir compte de r pour cal-
culer iP ; quelle est la valeur de iP ? Conclusion ?
III-2) A l'instant t1 = tMAX, on ouvre l'interrupteur k. La diode D a une tension de seuil
VS = 0,8V et une résistance interne négligeable (figure 4).