TP4: La lumière... onde ou particules

TP4: La lumière... onde ou particules ?
1. Les sources de lumière:
• Les lampes à incandescence sont constituées par un filament métallique porté à haute température par le
passage d’un courant électrique. Ces lampes consomment beaucoup d’énergie car elles chauffent (émission
d’infrarouge) plus qu’elles n’éclairent.
Elles émettent toutes les couleurs de l’arc en ciel, et leur
spectre d’émission est un spectre continu.
Toutefois la lumière violette est de moins en moins émise
lorsque la température diminue.
• Les lampes spectrales de type « néon » contenant un gaz à travers lequel jaillit une décharge électrique.
Ces lampes sont économes en énergie car elles chauffent beaucoup moins que les lampes à incandescence.
Elles émettent quelques couleurs seulement et leur spectre d’émission est un spectre discontinu constitué
par quelques raies colorées sur un fond noir.
Les longueurs d’onde des couleurs émises sont caractéristiques
du gaz présent dans le tube, et permettent d’identifier ce gaz.
La synthèse additive de ces couleurs réalisée par notre cerveau conduit à une impression de blanc.
• Le laser émet un faisceau très étroit, constitué de rayons lumineux parallèles entre eux, contrairement aux
autres lampes qui éclairent dans toutes les directions.
Son spectre n’est constitué que d’une seule couleur : c’est une source de lumière monochromatique.,
contrairement aux autres lampes qui sont polychromatiques (émission de plusieurs couleurs).
• Les DEL (diode électroluminescente) peuvent être mono ou polychromatiques, et ne chauffent
pratiquement pas. Ce sont des sources de lumière très économes, mais leur puissance est encore limitée.
• Une étoile est une énorme boule de gaz très chaud. La lumière qui nous parvient est issue de la surface de
l’étoile appelée photosphère : c’est la partie visible de l’étoile.
La photosphère est comparable au filament d’une lampe à incandescence : elle émet un spectre continu.
La quantité de lumière émise par l’étoile pour chaque couleur dépend uniquement de sa température.
Autour de la photosphère se trouve une couche de gaz sous faible pression, appelée chromosphère.
Ces gaz absorbent certaines couleurs, et le spectre de la lumière stellaire est donc un spectre d’absorption.
En déterminant les longueurs d’onde des couleurs absorbées par la
chromosphère, on peut déduire la nature des gaz qui y sont présents.
2. La loi de Wien:
Un corps chaud émet un rayonnement électromagnétique que
l'on appelle rayonnement thermique dont le spectre est continu
mais l'intensité lumineuse associée à chaque longueur d'onde
dépend de la température.
• Comment évolue le spectre de la lumière émise par un corps
chaud lorsque sa température augmente ?
Ceci est-il en accord avec les spectres de la lampe à incandescence
donnés ci-dessus ?
1

intensité
lumineuse
La loi de Wien relie la température T du corps chaud et la longueur d'onde λ
max
de son maximum d'émission.
T
x
λ
max
= 2,9.10
–3
en K.m
avec
T(K) = θ(°C) + 273
Ainsi notre soleil émet un maximum de lumière dans le jaune-vert,
correspondant à une longueur d’onde λ
max
= 0,50µm.
Déduis-en la température de sa photosphère en °C.
Les étoiles plus chaudes que le soleil émettent de la lumière
surtout dans le ..............
Les étoiles plus froides que le soleil émettent de la lumière
surtout dans le ..............
3. La "catastrophe ultraviolette":
Les courbes ci-dessus représentant les variations de l'intensité lumineuse en fonction de la longueur d'onde de la
lumière émise par un corps chaud sont tracées à partir de mesures expérimentales.
Mais elles sont en contradiction avec ce que prévoit la théorie si on
considère la lumière comme une onde !
Quelles sont ces contradictions ?
Quel domaine spectral (visible, IR , UV) est le plus concerné ?
Pour essayer de faire correspondre le modèle et l'expérience, le physicien allemand Max Planck suggère en l'an
1900 que les échanges d'énergie entre le corps chaud et le rayonnement qu'il émet se font, non pas de façon
continue, mais de façon discontinue, par "paquets d'énergie" appelés photons.
L'énergie E véhiculée par les photons est proportionnelle à la fréquence
ν
de l'onde associée:
E = h
x
ν
La relation entre la fréquence
ν
de l'onde (en Hz), sa longueur d'onde
λ
(en m)
et la célérité
c
de la lumière
dans le milieu de propagation étudié est :
ν
=
c / λ
avec
c
=
3,0.10
8
m.s
–1
dans le vide ou dans l'air.
La constante de Planck h a pour valeur : h = 6,62.10
–34
J.s et l'énergie E du photon s'exprime en Joule (J).
• Calcule l'énergie d'un photon associé à une radiation lumineuse rouge de longueur d'onde
λ
= 750nm.
• Même question pour un photon associé à une radiation lumineuse violette de longueur d'onde
λ
= 450nm.
4. L'effet photoélectrique:
En 1905, Albert Einstein reprend l'idée de Max Planck pour interpréter un autre phénomène que le modèle
ondulatoire de la lumière ne permettait pas d'expliquer : l'effet photoélectrique.
L'hypothèse de l'existence du photon semble alors s'imposer... essayons de comprendre pourquoi.
λ en µm

Description de l'expérience:
Une plaque métallique, appelée cathode, peut être éclairé par un faisceau
On peut modifier l'intensité I de ce faisceau lumineux.
Une autre plaque conductrice (anode) est présente en face de la cathode.
La cathode et l'anode sont fixées dans une ampoule en verre vidée d'air.
• Un courant électrique peut-il à priori circuler dans ce circuit ? pourquoi ?
• Qu'observe-t-on si on éclaire la cathode avec de la lumière bleue ?
• Comment se modifie cette observation si on diminue l'intensité du faisceau bleu qui éclaire la cathode ?
• Dans quel sens circule le courant électrique dans ce circuit ? et les électrons ?
Dans la cathode, les électrons sont liés par des forces électriques aux noyaux des atomes auxquels ils
appartiennent. Pour les arracher à la matière, il faut leur fournir une énergie minimale E
0
qui dépend de la
nature du métal utilisé.
Si les électrons reçoivent une énergie supérieure à E
0
, ils quittent la cathode avec une certaine énergie
cinétique qui peut leur permettre d'atteindre l'anode située à proximité.
• D'où provient l'énergie qui permet aux électrons de quitter la cathode et d'atteindre l'anode ?
• Pourquoi un courant électrique circule-t-il dans l'ampèremètre (les électrons pourraient rester sur l'anode) ?
• Nos observations peuvent-elles s'expliquer si on considère la lumière comme une onde, que l'on assimilera à
une vague à la surface de l'eau, d'amplitude variable ?
• On éclaire maintenant la cathode avec de la lumière rouge... les observations sont-elles les mêmes qu'avec la
lumière bleue ?
• Le modèle ondulatoire de la lumière permet-il d'expliquer ces observations ?
• Essayez d'interpréter l'ensemble des observations en utilisant le modèle corpusculaire de la lumière.
lumineux monochromatique de fréquence
ν
ajustable.
2

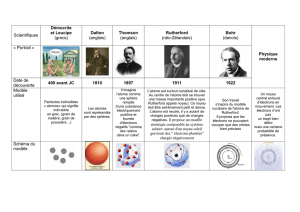
5. Quantification des niveaux d'énergie d'un atome:
Rappels du cours de seconde:
L’essentiel de la masse d’un atome est concentrée en son centre, appelé noyau.
Autour du noyau, des électrons se déplacent d’un mouvement incessant et désordonné,
dans un espace vide appelé nuage électronique.
Les limites de l’atome correspondent à un espace sphérique dans lequel on a 95% de
chances de trouver les électrons.
Ordre de grandeur de la taille du noyau : 10
–15
m de l’atome : 10
–10
m soit 100.000 fois plus grand.
Tous les électrons qui constituent le nuage électronique d’un atome ne sont pas, en moyenne, à la même
distance du noyau.
On peut ainsi classer les électrons en plusieurs groupes, chaque groupe se trouvant sur une couche plus ou
moins éloignée du noyau.
La couche la plus proche du noyau est notée « couche K », la suivante « couche L », etc…
Règles de remplissage des couches électroniques :
* les électrons se mettent en priorité sur les couches les plus proches du noyau, mais…
* le nombre de places disponibles sur une couche est limité : K 2 places L 8 places M 18 places
Remarque: les couches portent aussi le nom de "niveaux d'énergie" car plus les électrons sont proches du
noyau plus il faut leur fournir de l'énergie pour les arracher à l'atome, c'est à dire pour vaincre les forces
électriques qui les retiennent liés au noyau.
On dit que les niveaux d'énergie des électrons d'un atome sont quantifiés, c'est à dire que l'énergie d'un
électron ne peut pas varier de façon continue, mais qu'elle ne peut prendre que quelques valeurs particulières
associées aux couches électroniques K, L, M, ...
Exemple de l'atome d'hydrogène:
Les niveaux d’énergie de l’atome d’hydrogène vérifient la relation E
n
= −
−−
−13,6/n
2
avec E
n
en eV (1 eV= 1,60.10
–19
J) et n ∈
∈∈
∈ N*
n est appelé nombre quantique principal ( n=1 → niveau K, n=2 → niveau L, …)
Grâce à un apport d’énergie extérieur, sous forme de lumière ou par collision avec
une particule matérielle (électron,…), l’atome peut passer de son état fondamental
à un niveau d’énergie plus élevé, et se trouver ainsi dans un état excité.
Les états excités sont instables: l’atome se désexcite spontanément vers un des états
associés à un niveau d’énergie inférieur, en cédant de l’énergie.
En une ou plusieurs étapes appelées transitions, il retourne vers son état fondamental.
Lors d’une transition atomique d’un niveau d’énergie E
i
vers un niveau d’énergie E
j
l’atome absorbe ou émet un photon unique d’énergie E = I E
i
− E
j
I = hν
νν
ν
qui correspond à une onde électromagnétique de fréquence ν
νν
ν = I E
i
− E
j
I
/
h .
Application numérique :
Lors d’une transition électronique de n = 3 vers n = 2, l’énergie libérée est E = –1,5 – (–3,4) = 1,9eV
soit en Joule : E = 1,9
x
1,60.10
–19
= 3,04.10
–19
J
La fréquence de l’onde émise est :
ν
νν
ν
= E / h = 3,04.10
–19
/ 6,62.10
–34
= 4,59.10
14
Hz
Et sa longueur d’onde : λ
λλ
λ =
c
/
ν
νν
ν
= 3,00.10
8
/ 4,59.10
14
= 6,53.10
–7
m soit 653 pm (lumière visible rouge)
–
13,6
–
3,4
–
1,5
–
0,9
–
0,5
Etat fondamental
Etats excités
0
E en eV
absorption
d’énergie
émission
d’énergie
n=1
n=2
n=3
Longueur d’onde
λ
λλ
λ
Infrarouge
Ondes radio
ultraviolet
Rayons X
Rayons
γ
visible
400nm 800nm
3

D
θ
en rad
Les spectres d’émission et d’absorption d’un atome sont donc complémentaires : un atome est capable
d’absorber des ondes lumineuses de mêmes fréquences que celles qu’il est susceptible d’émettre.
Pour observer le spectre d’une source de lumière, il faut positionner devant elle une « fente » (écran noir
percé d’un trou rectangulaire vertical et étroit), puis une lentille convergente qui forme l’image de cette fente
sur un écran de projection, et entre la lentille et l’écran un prisme en verre ou un réseau :
Spectre d’émission : Si on excite du gaz dihydrogène en faisant passer une décharge électrique dans ce gaz, on
constate qu’il émet de la lumière pour certaines couleurs
(longueurs d’onde) particulières : c’est un spectre de raies
Une lampe à incandescence émet toutes les couleurs présentes
dans l’arc en ciel : son spectre d’émission est continu
Spectre d’absorption: En
intercalant
sur
le
trajet
de
la
lumière
une
ampoule
en
verre
contenant
du
dihydrogène,
on constate que certaines couleurs sont absorbées par les
atomes qui constituent ce gaz : elles apparaissent en noir
sur le fond continu correspondant à la lampe à incandescence.
6. Le modèle ondulatoire de la lumière doit-il être abandonné ?
Le modèle ondulatoire ne permet pas d'expliquer les échanges d'énergie entre la matière et la lumière.
Mais le modèle corpusculaire ne permet pas d'expliquer certains comportements de la lumière comme par
exemple le phénomène d'interférence ou de diffraction qui est spécifique aux ondes!
Phénomène de diffraction:
Lorsqu’une onde progressive plane de longueur d’onde λ
λλ
λ rencontre une ouverture étroite
(ou un obstacle étroit), de largeur a comparable à λ
λλ
λ , le faisceau devient divergent,
d’autant plus que la dimension a de l’ouverture est petite.
Le phénomène de diffraction est spécifique aux ondes.
La lumière, qui est diffractée par un fil ou une fente, est donc une onde.
• Qu'observe-t-on sur l'écran lorsqu'un faisceau laser rencontre
une fente ou un fil ?
• Que devrait-on observer si le faisceau était constitué de photons assimilables à des boules de petites
dimensions comparativement à la largeur de la fente ?
Comment concilier ces deux aspects de la lumière: onde et corpuscule ?
• Qu'observe-t-on sur l'écran lorsque l'intensité lumineuse du laser diminue, au point que les photons sont émis
les uns après les autres ?
4
θ
=
λ
λλ
λ
a
θ
en radian
λ
et a en m
 6
6
1
/
6
100%