Resumé cours atome

1
Première partie : Structure de l’atome
Introduction
L’écriture d’une formule aussi bien admise actuellement que H2O cache des notions très lointaines de
l’observation immédiate et de l’intuition, et des concepts complexes qui ont eu du mal à trouver l’adhésion
générale de la communauté. Les modèles de l’atome et de la molécule, associés à la distinction entre
élément chimique et corps simple, ont mis longtemps pour émerger.
I. A partir de l’antiquité, deux avancées cruciales vers un modèle où l’atome possède une structure :
découvertes de l’électron puis du noyau.
1. Les philosophes grecs avaient conçu deux systèmes théoriques pour expliquer la matière et ses
transformations : théories des éléments et théories atomiques. (< constat de l’existence d’invariants)
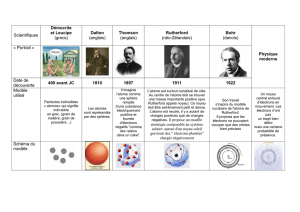
2. John Dalton (1766-1844) propose une nouvelle hypothèse atomique (1804) : les combinaisons chimiques
se font par unités discrètes, atome par atome, et les atomes d’un même élément sont identiques, et une loi
des proportions multiples : deux éléments peuvent se combiner de diverses façons ; si le poids de l’un est
pris comme référence, les poids de l’autre dans les combinaisons possibles sont entre eux dans des
proportions simples. Les atomes et leurs combinaisons sont représentés à l’aide de symboles. (< lois de
proportions)
3. Amedeo Avogadro (1778-1856) propose en 1811 une loi sur les volumes, énoncée indépendamment par
André-Marie Ampère (1775-1836) en 1814 : « Dans les mêmes conditions de température et de pression,
des volumes égaux de gaz différents contiennent le même nombre de molécules. ». Il associe plusieurs
hypothèses qui jettent les bases de la théorie atomique moderne : (i) les particules les plus petites des gaz
ne sont pas obligatoirement des atomes, (ii) il doit y avoir division des molécules lors d’une réaction
chimique.
4. Joseph John Thomson (1856-1940) découvre l’électron (1897) puis effectue la mesure de la charge
électronique (1898-1899). Il propose un modèle globulaire de l’atome : une boule d’électricité positive à
l’intérieur de laquelle gravitent les électrons (1903). Il reçoit le prix Nobel de physique en 1906.
5. Ernest Rutherford (1871-1937) découvre les rayonnements α et β émis par l’uranium (1899) et reçoit le
prix Nobel de chimie « pour ses recherches sur la désintégration des éléments et la chimie des substances
radioactives » (1908).
Les particules α sont identifiées comme des atomes d’hélium portant une double charge positive (1908).
Rutherford pressent que ces particules chargées et hautement énergétiques devraient pouvoir servir de
sonde pour l’étude de la structure de l’atome, supposé le siège de forces électriques très intenses. Il réalise
une série d’expériences avec Hans Geiger et Ernest Marsden consistant à étudier l’interaction entre un
faisceau de particules α et une feuille métallique de faible épaisseur. Les résultats sont inattendus :
l’essentiel du faisceau passe directement à travers la feuille, très légèrement dévié, et un certain nombre de
particules rebondissent sur la feuille à un angle de 90° et plus. Leur interprétation conclut au caractère
lacunaire de l’atome et à l’invention du noyau : les particules α sont des noyaux d’hélium (1909) et l’atome
peut être décrit comme analogue au système solaire, un noyau central unique chargé positivement et
entouré d’électrons gravitant sur des trajectoires circulaires (1911).

2
échantillon de radium,
source de
particules α
faisceau non dévié
écran fluorescent
en sulfure de zinc
feuille d'or
d'épaisseur 0,6 μm
faisceau dévié
noyau atome d'or
particule non déviée
particule déviée
II. Etape suivante dans l’évolution du modèle de l’atome : introduction de la quantification ;
spectroscopie et modèle de Bohr
Introduction de la quantification : les grandeurs associées aux particules de l’infiniment petit ne varient pas
de manière continue ; matière et rayonnement ne doivent pas être traités séparément.
1. Max Planck (1858-1947) développe la théorie des quanta (1900) et définit une nouvelle constante, le
quantum d’action h (constante de Planck) pour interpréter les échanges d’énergie entre la matière et le
rayonnement : les absorptions ou émissions d’énergie se font par quantités discrètes, multiples d’une
quantité h.ν pour une lumière monochromatique de fréquence ν ; plus la fréquence de la radiation est
grande, plus le quantum correspondant contient de l’énergie. Prix Nobel de physique en 1918.
h : référence pour savoir si un objet peut être étudié avec la physique classique ou bien s’il doit être étudié
avec la physique quantique ; comparer une grandeur relative à l’objet dans les conditions de l’étude et ayant
les dimensions de h. valeur numérique : connaître l’ordre de grandeur (6,62.10-34 J.s)
2. Albert Einstein (1879-1955) extrapole l’hypothèse des quanta de Planck et fournit une interprétation de
l’effet photoélectrique (1905).
L’effet photoélectrique découvert par Heinrich Hertz (1857-1894) en 1887 consiste en l’émission d’électrons
(détectés par le courant qu’ils transportent) par un métal lorsque de la lumière d’une fréquence supérieure à
une fréquence seuil frappe la surface de l’échantillon. Le fait que le courant (proportionnel au nombre
d’électrons arrachés à chaque seconde) soit proportionnel à l’intensité du rayonnement incident traduisait la
conservation de l’énergie ; par contre l’effet de « tout ou rien » restait inexpliqué.
courant photoélectrique
0
énergie des photons h.ν
0
énergie cinétique des photoélectrons Ec
h.ν0
W = h.ν0
h.ν = W + Ec
énergie des photons h.ν
h.ν0
L’interprétation repose sur l’idée que l’énergie de la lumière est transportée par fractions discrètes : un
rayonnement monochromatique de fréquence ν est constitué de grains d’énergie, les photons, particules de
masse nulle se déplaçant dans le vide à la vitesse de la lumière c, et possédant une énergie ε = h.ν et une
quantité de mouvement p = h.ν/c ; l’énergie arrive en « grains d’énergie » et l’émission d’un électron ne peut
se produire que par suite de l’interaction avec un grain d’énergie au moins égale au travail d’extraction W.

3
Les électrons éjectés par interaction avec des photons d’énergie supérieure à ce seuil, sont émis avec une
énergie cinétique.
Le prix Nobel de physique est attribué à Einstein en 1921, pour la loi photoélectrique et ses travaux dans le
domaine de la physique théorique.
3. Heinrich Geissler (1815-1879) est l’inventeur de tubes dits « de Geissler » permettant la caractérisation
des gaz et contribue ainsi à l’essor de la « spectroscopie » (1856) ; il met au point la première pompe à vide
à mercure permettant d’obtenir une pression de l’ordre du centième de millimètre de mercure (1857).
Un tube de Geissler possède à ses extrémités des électrodes entre lesquelles est appliquée une différence
de potentiel (ddp) croissante. A l’intérieur d’un tel tube, un gaz sous faible pression (1,5 mbar) conduit à un
mélange d’électrons, ions positifs, molécules et atomes ; ces atomes sont excités lors de collisions et se
désexcitent avec émission de radiations électromagnétiques. Pour une certaine valeur de la ddp, on observe
le passage d’un courant électrique et le tube devient luminescent. On appelle « spectre atomique
d’émission » le résultat de l’analyse de la lumière produite, exprimé par la succession des valeurs des
énergies, fréquences, nombres d’onde ou longueurs d’onde qui composent cette lumière. Chacune de ces
valeurs caractérise une « raie spectrale ». Relations entre les grandeurs caractérisant une raie (important) :
ΔE = h.v = h.c.(1/λ) = h.c.σ
fréquence ν
nombre d'onde σ
longueur d'onde λE = h.ν = h.c.σ = (h.c)/λ
énergie E
4. Johann Jakob Balmer (1825-1898) a établi empiriquement (1885) une formule de récurrence reliant les
longueurs d’onde des quatre raies alors connues du spectre atomique d’émission de l’hydrogène, 656 nm,
486 nm, 434 nm, 410 nm (dans le domaine du visible). Cette « série » de raies est nommée série de Balmer.
=
1
λConstante. m2m entier, m > 2
m2 - 4
La formule de Balmer a servi de modèle pour l’expression des lois donnant les raies spectrales des autres
séries du spectre (domaines situés de part et d’autre du visible, l’infrarouge et l’ultraviolet).
=
1
λR22
1
m2
1
()
Balmer, visible, m > 2
=
1
λR32
1
m2
1
()
Paschen, infrarouge, m > 3
=
1
λR12
1
m2
1
()
Lyman, ultraviolet, m > 1
La symétrie algébrique de ces formules a confirmé une intuition de Walter Ritz, exprimée dans un principe
de combinaison (principe de Ritz) : les deux termes de la formule de Balmer ont des existences propres.
=n2
1
λn,m
R1
m2
1
-
(
n et m entiers, m > n
)
Johannes Robert Rydberg (1854-1919), en étudiant les spectres de divers éléments chimiques, a mis en
évidence l’importance de la constante R qui intervient dans cette loi et dont la valeur peut être obtenue avec
une grande précision par la position des raies spectrales. Cette constante est appelée constante de Rydberg
et sa valeur pour l’hydrogène est : RH = 10979708,014 ± 0,013 m-1.
Spectroscopie d’émission atomique. Le spectre d’émission atomique d’un élément est toujours constitué des
mêmes raies : il est caractéristique de cet élément.

4
Principe de combinaison de Ritz (Walter Ritz) : les deux termes de la formule de Balmer ont des existences
propres.
=n2
1
λn,m
R1
m2
1
-
(
n et m entiers, m > n
)
Constante de Rydberg pour l’hydrogène est : RH = 10979708,014 ± 0,013 m-1.
5. Niels Bohr (1885-1962) établit une synthèse entre l’existence d’un quantum d’action (issue de la théorie
du rayonnement thermique de Planck et de l’interprétation de l’effet photoélectrique par Einstein) et le noyau
atomique de Rutherford. Il produit un modèle quantifié de l’atome d’hydrogène (1913) vu comme un système
de deux particules : un électron de charge (-e) et de masse m décrivant une trajectoire circulaire plane de
rayon r autour d’un noyau fixe de charge (+e), qui résout certaines contradictions du modèle de Rutherford
et permet l’interprétation des données spectroscopiques expérimentales.
Postulats de base : (1) les orbites stationnaires (où l’émission de rayonnement est interdite) sont définies par
un équilibre dynamique entre la force d’attraction électrostatique entre noyau et électron donnée par la loi de
Coulomb et l’effet centrifuge du mouvement orbitalaire ; (2) dans un état stationnaire, le rapport de l’énergie
totale de l’électron à sa fréquence orbitalaire est un multiple entier de h/2 ; cette condition est équivalente à
une condition portant sur le moment cinétique orbital de l’électron qui doit être un multiple entier de h/2π :
r.m.v = nh/2π (les vecteurs position r et vitesse v sont orthogonaux), avec n entier ; (3) il y a émission
d’énergie seulement lorsqu’un électron subit une transition électronique entre deux orbites stationnaires, et
non pas de manière continue ; (4) la fréquence de la radiation émise lors d’une transition entre deux orbites
dont les énergies diffèrent de ΔE est ΔE/h.
Ça vaut la peine d'introduire déjà la notation de hbar,
= h/2
.
L’application du principe fondamental de la dynamique conduit à une expression de l’énergie totale En de
l’électron dans l’état caractérisé par le nombre n.
transition vers
un état plus lié:
stabilisation
absorption émission
E
E
transition vers
un état moins lié:
excitation
E
état
non lié
Em
En
Em
En
états
excités
état
fondamental
Em
En
E1
0
En = - me.e4
8ε02.h2.n2=n2
E1
ΔEm vers n =E1n2
1
m2
1
-
(
)
Les énergies sont comptées négativement.
La valeur n = 1 définit l’état le plus stable de l’atome, état fondamental. Les valeurs obtenues pour n = 1
sont : E1 = -13,60 eV et a0 = 0,529.10-10 m.
Une valeur de n > 1 définit un état où l’électron est moins fortement lié au noyau, appelé état excité. Lorsque
n tend vers l’infini, l’électron n’est plus lié au noyau: l‘atome est dans l’état ionisé. L’énergie (ou le potentiel)
d’ionisation, énergie minimale nécessaire à ce processus, est donc égale à -E1.
Une série de raies du spectre de l’atome d’hydrogène traduit ainsi un ensemble de transitions électroniques
vers un niveau final donné.

5
Les raies sont de plus en plus rapprochées et de moins en moins intenses vers les grandes énergies (faibles
longueurs d’onde), puisque les niveaux deviennent alors eux-mêmes de plus en plus rapprochés et les états
correspondants (de moins en moins liés) deviennent de moins en moins peuplés.
Les valeurs ainsi calculées pour les fréquences caractérisant les raies du spectre sont en excellent accord
avec les données expérimentales.
Modèle de Bohr : transitions Données expérimentales : séries du spectre
états initiaux état final nom de la série domaine de radiations
m ≥ 2 n = 1 Lyman ultraviolet lointain
m ≥ 3 n = 2 Balmer visible et ultraviolet
m ≥ 4 n = 3 Paschen infrarouge proche
m ≥ 5 n = 4 Brackett infrarouge
m ≥ 6 n = 5 Pfund infrarouge
Le modèle de Bohr est applicable également aux systèmes « hydrogénoïdes » (ressemblent à H), issus
d’atomes de numéro atomique Z par perte de (Z-1) électrons, qui sont donc des ions positifs constitués par
un noyau de charge Ze et un unique électron, telles les espèces He+ (Z = 2), Li2+ (Z = 3), Be3+ (Z = 4), B4+
(Z = 5) et U91+ (Z = 92). Les expressions obtenues pour l’énergie et le rayon d’une orbite traduisent une
stabilisation de l’unique électron du système par rapport à l’hydrogène (pour une même valeur de n,
l’énergie En et le rayon rn ont des valeurs inférieures à celles obtenues pour l’hydrogène).
Bohr reçoit le prix Nobel de physique en 1922.
III. Mesure de la masse des atomes et découverte de la structure du noyau ; isotopie
1. Francis William Aston (1877-1945) met au point le premier « spectrographe de masse » (1919) : les
atomes sont transformés en ions, à leur tour accélérés et soumis à l’action d’un champ électrique et d’un
champ magnétique, induisant une déviation de leur point d’impact sur une plaque photographique qui varie
comme le rapport masse/charge. Il établit l’existence de deux isotopes du néon, de masses atomiques 20 et
22 et dans des proportions 90% et 10%, faisant concorder les résultats de Thomson (proposant deux
masses pour le néon, 20 ou 22) et de Ramsay (observant une masse moyenne de 20,2). Le terme
« isotopes » avait été proposé par Soddy (1914) pour désigner les éléments radioactifs de même numéro
atomique et de masses différentes et qui avait posé la question de l’existence d’isotopes d’éléments non
radioactifs. James Chadwick (1891-1974), découvrant le neutron (1932), permet de préciser la structure du
noyau et d’interpréter l’existence d’isotopes.
Prix Nobel de chimie en 1904 : sir William Ramsay (1852-1916), « pour la découverte des gaz rares dans
l’air, leur détermination et leur placement dans la classification périodique des éléments » (découverte et
baptême successifs de l’argon, de l’hélium, du krypton, du néon et du xénon, constituant une nouvelle
famille du tableau périodique). Prix Nobel de chimie en 1921 : Frederick Soddy (1877-1956), « pour ses
contributions à la chimie des substances radioactives et ses recherches sur les origines et la nature des
isotopes ». Prix Nobel de chimie en 1922 : Francis William Aston (1877-1945), « pour sa découverte, grâce
au spectrographe de masse, d’un grand nombre d’isotopes élémentaires non radioactifs ainsi que pour
l’énoncé de la règle des entiers pour les masses atomiques ». Prix Nobel de physique en 1935 : James
Chadwick (1891-1974).
2. Stade de description pour cette année : les particules constitutives de l’atome sont le noyau, lui-même
constitué de nucléons, protons et neutrons, et les électrons. Un élément est caractérisé par son « numéro