INTRODUCTION AU TRAITEMENT NUMÉRIQUE DU SIGNAL

13
INTRODUCTION AU TRAITEMENT
NUMÉRIQUE DU SIGNAL
APERÇU DU CHAPITRE
13–1 Concepts de base du traitement numérique
du signal
13–2 Conversion de signaux analogiques sous forme
numérique
13–3 Méthodes de conversion analogique-numérique
13–4 Processeur de signal numérique (DSP)
13–5 Méthodes de conversion numérique-analogique
OBJECTIFS DU CHAPITRE
■Nommer les éléments essentiels d’un système de traitement
numérique du signal.
■Expliquer comment convertir des signaux analogiques sous
forme numérique.
■Discuter du rôle du filtrage.
■Décrire un processus d’échantillonnage.
■Expliquer l’utilité d’une conversion analogique-numérique.
■Décrire le fonctionnement d’un convertisseur analogique-
numérique (CAN).
13
INTRODUCTION AU TRAITEMENT
NUMÉRIQUE DU SIGNAL

■Convertisseur
analogique-numérique
(CAN)
■Processeur de signal
numérique (DSP)
■Convertisseur
numérique-analogique
(CNA)
■Échantillonnage
■Fréquence de Nyquist
■Distorsion de repliement
(aliasing)
■Quantification
■Cœur de DSP
■MIP/s
■Mégaflops
■MMAC/s
■Traitement pipeline
■Extraction
■Décodage
■Exécution
■Discuter de concepts de base d’un processeur de signal
numérique (DSP).
■Décrire l’architecture d’un processeur de signal numérique.
■Nommer différentes fonctions effectuées par un processeur de
signal numérique.
■Décrire l’utilité d’une conversion numérique-analogique.
■Décrire le fonctionnement d’un convertisseur numérique-
analogique (CNA).
743
INTRODUCTION
Le traitement numérique du signal est une technologie de
pointe utilisée à vaste échelle dans nombre d’applications
comme dans les automobiles, les appareils domestiques,
industriels, médicaux ou militaires, la reproduction d’images,
les télécommunications, l’instrumentation et bien d’autres.
Le traitement numérique du signal fait appel aux
mathématiques, à la programmation logicielle et à du
matériel informatique de traitement pour manipuler des
signaux analogiques. Il peut servir à améliorer la qualité
d’images, à compresser des données pour un stockage ou
des transmissions plus efficaces, dans la synthèse de la parole,
pour la reconnaissance vocale et ainsi de suite.
Ce chapitre présente un aperçu des nombreuses
possibilités du traitement numérique du signal. Une étude
approfondie de ce sujet nécessiterait beaucoup plus qu’un
simple chapitre; c’est pourquoi nous vous proposons une
liste d’ouvrages dédiés au traitement numérique du signal à
la fin de ce chapitre. Vous pouvez également obtenir les
données et fiches techniques des composants de la famille
TMS320 sur le site Web de Texas Instruments à www.ti.com,
de même que sur des processeurs de signaux numériques à
www.motorola.com et www.analogdevices.com.
CIRCUITS LOGIQUES À FONCTION FIXE
ADC0804
PROCESSEURS DE SIGNAUX NUMÉRIQUES
TMS320C62xx TMS320C64xx TMS320C67xx
TERMES CLÉS

744 ■INTRODUCTION AU TRAITEMENT NUMÉRIQUE DU SIGNAL
13–1CONCEPTS DE BASE DU TRAITEMENT NUMÉRIQUE DU SIGNAL
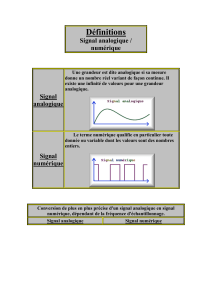
Le traitement numérique du signal permet de convertir des signaux captés sous leur
forme analogique naturelle (sons, vidéo et informations de détecteurs) en données
numériques et incorpore des techniques de correction et de modification des données
de signaux analogiques pour différentes applications.
Après l’étude de cette section, vous pourrez
■Définir un convertisseur analogique-numérique (CAN) ■Définir un processeur
de signal numérique (DSP) ■Définir un convertisseur numérique-analogique (CNA)
■Dessiner le schéma de principe d’un système de traitement numérique du signal
Un système de traitement numérique du signal convertit d’abord des données analo-
giques en une suite de niveaux distincts. La forme graphique d’une telle séquence de
niveaux représentant les variations du signal analogique ressemble à un escalier, comme le
montre la figure 13–1. Le processus de modification du signal analogique en une approxi-
mation « en escalier » est accompli par un circuit échantillonneur bloqueur.
L’approximation en forme d’escalier est ensuite quantifiée en une suite de codes
binaires, où chacun de ces codes définit une marche particulière de l’escalier, grâce à un
processus appelé conversion analogique-numérique. Le circuit responsable de cette
transformation est le convertisseur analogique-numérique (CAN).
Une fois converti sous forme numérique, le signal analogique est dirigé vers un
processeur de signal numérique (DSP). Un DSP peut effectuer différents traitements sur les
données entrantes : élimination d’interférences parasites, augmentation ou réduction en
amplitude de certaines fréquences du signal, codage de données pour des transmissions plus
sûres, détection et correction d’erreurs dans les codes transmis et ainsi de suite. Un DSP
peut servir, entre autres, à corriger des enregistrements sonores, à éliminer l’effet d’écho
sur des lignes de communication, à augmenter la précision d’images de tomodensito-
grammes pour des diagnostics médicaux plus précis ou à brouiller les conversations au
téléphone cellulaire pour le droit au domaine privé.
Une fois traités par le DSP, les signaux peuvent être reconvertis en une version améliorée
du signal analogique d’origine par un convertisseur numérique-analogique (CNA). La
figure 13–2 montre le schéma de principe d’un système de traitement numérique du signal.
En réalité, les DSP sont des microprocesseurs spécialisés, sensiblement différents des
microprocesseurs d’usage général. Contrairement à ces derniers qui fonctionnent avec des
Chaque niveau maintenu est
converti en un code binaire
par le CAN.
Maintien
Échantillon
FIGURE 13–1
Signal analogique original
(onde sinusoïdale) et son
approximation « en escalier ».
Signal
analogique CAN DSP CNA Filtre de reconstruction
Circuit
échantillonneur
bloqueur
Filtre anti-
repliement
Signal
analogique
corrigé
10110
01101
00011
11100
10110
01101
00011
11100
FIGURE 13–2
Schéma de principe d’un système de
traitement numérique du signal.

CONVERSION DE SIGNAUX ANALOGIQUES SOUS FORME NUMÉRIQUE ■745
logiciels complexes afin d’accomplir un grand nombre de tâches génériques, les
processeurs de signaux numériques servent dans des applications spécialisées. Les DSP
peuvent ainsi dévorer d’imposantes quantités de nombres beaucoup plus rapidement et
travailler en temps réel, en traitant les informations à mesure qu’elles se produisent grâce à
des algorithmes spéciaux. D’une part, le convertisseur analogique-numérique (CAN) d’un
système doit être en mesure d’échantillonner les données entrantes à une vitesse suffisante
pour calquer toutes les variations importantes de l’amplitude du signal. D’autre part, le DSP
doit être capable de suivre la vitesse d’échantillonnage du CAN et accomplir ses calculs à
une vitesse égale ou supérieure au flux de données échantillonnées qu’il reçoit. Une fois
traitées par le DSP, les données numériques sont dirigées vers un convertisseur numérique-
analogique (CNA) pour être reconverties sous forme analogique.
13–2CONVERSION DE SIGNAUX ANALOGIQUES SOUS FORME NUMÉRIQUE
Avant de traiter des signaux à l’aide de techniques numériques, il faut d’abord convertir
le signal analogique sous une forme numérique.
Après l’étude de cette section, vous pourrez
■Expliquer le processus de base de conversion d’un signal analogique sous forme
numérique ■Décrire l’utilité d’un circuit échantillonneur bloqueur ■Définir la fréquence
de Nyquist ■Expliquer les causes de la distorsion de repliement (aliasing) et comment
l’éliminer ■Décrire le rôle d’un convertisseur analogique-numérique (CAN)
Filtrage et échantillonnage
Les deux premiers blocs du schéma de principe de la figure 13–2 correspondent à un filtre
anti-repliement et à un circuit échantillonneur bloqueur. Ce dernier circuit joue deux rôles,
le premier étant l’échantillonnage. L’échantillonnage désigne le processus de capture d’un
nombre suffisant de valeurs discrètes en différents points d’une forme d’onde, afin de la
représenter numériquement. Plus le nombre d’échantillons est élevé, plus la forme d’onde
sera reproduite avec précision. L’échantillonnage convertit ainsi un signal analogique en
une suite d’impulsions, où chacune d’elles représente l’amplitude du signal à un moment
précis. La figure 13–3 illustre le principe de l’échantillonnage.
Avant d’échantillonner un signal analogique, il faut respecter certains critères afin d’obtenir
une représentation fidèle du signal d’origine. À l’exception des ondes sinusoïdales pures, tout
signal analogique se compose d’un spectre de fréquences composites appelées harmoniques.
Les harmoniques d’un signal analogique sont en fait des ondes sinusoïdales, chacune d’une
fréquence et d’une amplitude distincte. C’est ainsi qu’en combinant les harmoniques d’une
forme d’onde périodique donnée, on peut obtenir le signal original. Cependant, tout signal à
échantillonner doit d’abord traverser un filtre passe-bas anti-repliement pour éliminer les
harmoniques de fréquences supérieures à une certaine valeur nommée fréquence de Nyquist.
Théorème de l’échantillonnage Notez la présence de deux formes d’ondes d’entrée à la
figure 13–3, l’une représentant le signal analogique et l’autre la forme d’onde des
impulsions d’échantillonnage. L’une des règles de l’échantillonnage stipule que pour
reproduire adéquatement un signal analogique, la vitesse d’échantillonnage doit être
1. Qu’est-ce qu’un DSP?
2. Que signifie l’abréviation CAN?
3. Que désigne l’abréviation CNA?
4. Quel type de circuit peut transformer un signal analogique sous forme binaire?
5. Quel type de circuit peut transformer un signal numérique sous forme analogique?
SECTION 13–1
RÉVISION
Les réponses se retrouvent
à la fin du chapitre.

746 ■INTRODUCTION AU TRAITEMENT NUMÉRIQUE DU SIGNAL
supérieure au double de la composante de fréquence la plus élevée contenue dans le signal
analogique, fa(max). En d’autres termes, la fréquence analogique la plus élevée ne doit pas
dépasser la moitié du taux d’échantillonnage. L’équation 13–1 donne le calcul pour la
fréquence fa(max), connue sous le nom de fréquence de Nyquist.
féchantillonnage ≥2fa(max)
Pour mieux comprendre le théorème de l’échantillonnage, nous pouvons faire appel à la
simple analogie d’une balle qui rebondit. Même si cette comparaison n’offre pas une
représentation très précise de l’échantillonnage de signaux électriques, elle permet
d’illustrer le principe de base. Si vous prenez une seule photo (échantillon) d’une balle alors
qu’elle rebondit, comme le montre la figure 13–4 a), vous pouvez voir qu’elle est suspendue
au-dessus du sol, mais vous ne pouvez rien déduire de son parcours. Il vous est impossible
de déterminer si la balle monte ou descend, ni deviner la courbe de son bond. Maintenant,
si vous photographiez cette balle à deux intervalles égaux pendant qu’elle rebondit comme
à la partie b), vous obtenez un minimum d’informations sur son mouvement, mais aucune
indication sur la courbe de son bond. Ici, vous pourriez déduire que la balle demeure à une
certaine hauteur d’une photo à l’autre et que sa hauteur maximale est sans doute supérieure
à ce que vous apercevez sur chaque photographie. Enfin, si vous photographiez cette balle
quatre fois comme à la partie c), vous pouvez commencer à voir plus clairement la véritable
trajectoire de la balle alors qu’elle rebondit. En conséquence, plus vous prenez de photos
(échantillons), plus il vous est facile de déterminer le parcours de la balle lors de son bond.
Équation 13–1
Circuit
d’échantillonnage
Version
échantillonnée du
signal d’entrée
Signal
d’entrée
analogique
Impulsions
d’échantillonnage
FIGURE 13–3
Principe de l’échantillonnage.
a) Échantillon unique du saut d’une balle. b) Deux échantillons d’une balle pendant son
saut donne un minimum d’informations
sur son déplacement, sans toutefois décrire
clairement son parcours.
c) Quatre échantillons d’une balle alors
qu’elle rebondit crée une image plus
précise de sa véritable trajectoire.
FIGURE 13–4
Analogie simple de la théorie de
l’échantillonnage.