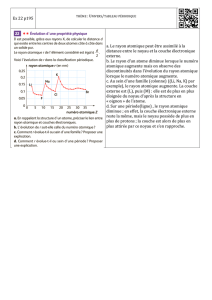
Classification periodique des elements

- 1 -
TD N°4 & 5
CLASSIFICATION PERIODIQUE DES ELEMENTS
EXERCICE 1
CALCUL DE COEFFICIENTS D’ECRAN
A Structure électronique
12
3
21][ ssLi =
22
4
21][ ssBe =
122
5
221][ pssB =
222
6
221][ pssC =
322
7
221][ pssN =
422
8
221][ pssO =
522
9
221][ pssF =
622
10
221][ pssNe =
B Coefficients d’écran et numéros atomiques effectifs
Pour les atomes polyélectroniques, l’existence de forces de répulsion inter-électroniques
ne permet pas d’utiliser le modèle de Bohr.
La méthode de Slater consiste à considérer que l’ensemble des interactions électrostatiques
s’exerçant sur un électron donné (attraction du noyau et répulsion des autres électrons) peut se
ramener à une seule interaction attractive avec le noyau « écranté » par les électrons situés
entre le noyau et l’électron. La charge Z du noyau devient alors une charge effective Z*
relative à l’électron :
∑
−= σ ZZ
eff
*
∑
σ : constante d’écran de tous les autres électrons
• Lithium :
12
3
21][ ssLi =
 Groupe 1s
Coefficient d’écran : 31,0
1
= σ
Numéro atomique effectif : 69,231,03
*
1,
=−=
eff
Z
 Groupe 2s2p
Coefficient d’écran : 7,1285,0
2
=×= σ
Numéro atomique effectif : 3,17,13
*
2,
=−=
eff
Z

- 2 -
La charge effective pour un électron externe est inférieure à la charge effective pour un
électron de cœur, car l’écrantage du noyau est plus important.
• Beryllium :
22
4
21][ ssBe =
 Groupe 1s
Coefficient d’écran : 31,0
1
= σ
Numéro atomique effectif : 69,331,04
*
1,
=−=
eff
Z
 Groupe 2s2p
Coefficient d’écran : 05,235,0285,0
2
=+×= σ
Numéro atomique effectif : 95,105,24
*
2,
=−=
eff
Z
• Bore :
122
5
221][ pssB =
 Groupe 1s
Coefficient d’écran : 31,0
1
= σ
Numéro atomique effectif : 69,431,05
*
1,
=−=
eff
Z
 Groupe 2s2p
Coefficient d’écran : 4,2235,0285,0
2
=×+×= σ
Numéro atomique effectif : 6,24,25
*
2,
=−=
eff
Z
• Carbone :
222
6
221][ pssC =
 Groupe 1s
Coefficient d’écran : 31,0
1
= σ
Numéro atomique effectif : 69,531,06
*
1,
=−=
eff
Z
 Groupe 2s2p
Coefficient d’écran : 75,2335,0285,0
2
=×+×= σ
Numéro atomique effectif : 25,375,26
*
2,
=−=
eff
Z
• Azote :
322
7
221][ pssN =
 Groupe 1s
Coefficient d’écran : 31,0
1
= σ
Numéro atomique effectif : 69,631,07
*
1,
=−=
eff
Z

- 3 -
 Groupe 2s2p
Coefficient d’écran : 1,3435,0285,0
2
=×+×= σ
Numéro atomique effectif : 9,31,37
*
2,
=−=
eff
Z
• Oxygène :
422
8
221][ pssO =
 Groupe 1s
Coefficient d’écran : 31,0
1
= σ
Numéro atomique effectif : 69,731,08
*
1,
=−=
eff
Z
 Groupe 2s2p
Coefficient d’écran : 45,3535,0285,0
2
=×+×= σ
Numéro atomique effectif : 55,445,38
*
2,
=−=
eff
Z
• Fluor :
522
9
221][ pssF =
 Groupe 1s
Coefficient d’écran : 31,0
1
= σ
Numéro atomique effectif : 69,831,09
*
1,
=−=
eff
Z
 Groupe 2s2p
Coefficient d’écran : 8,3635,0285,0
2
=×+×= σ
Numéro atomique effectif : 2,58,39
*
2,
=−=
eff
Z
• Néon :
622
10
221][ pssNe =
 Groupe 1s
Coefficient d’écran : 31,0
1
= σ
Numéro atomique effectif : 69,931,010
*
1,
=−=
eff
Z
 Groupe 2s2p
Coefficient d’écran : 15,4735,0285,0
2
=×+×= σ
Numéro atomique effectif : 85,515,410
*
2,
=−=
eff
Z

- 4 -
C Rayon atomique
Dans le modèle de Slater, le rayon atomique est donné par :
0
*
2*
)( a
Z
n
r
eff
=
n* : nombre quantique apparent des électrons de valence
Z* : numéro atomique effectif des électrons de valence
pma 53
0
= : rayon de la première orbite de Bohr
Jusqu’à n = 3, n* = n
Ici, les électrons de valence sont situés sur la couche 2s2p donc :
)(
212
53
2
*
2,
*
2,
2
pm
ZZ
r
effeff
=×=
Application numérique :
pmLir 163
30,1
212
)( ==
pmBer 109
95,1
212
)( ==
pmBr 82
60,2
212
)( ==
pmCr 65
25,3
212
)( ==
pmNr 54
90,3
212
)( ==
pmOr 47
55,4
212
)( ==
pmFr 41
20,5
212
)( ==
pmNer 36
85,5
212
)( ==
Tableau récapitulatif
Atome Z Structure électronique Groupe 1s Groupe 2s2p Rayon (pm)
1
σ
*
1, eff
Z
2
σ
*
2, eff
Z
Li 3
12
3
21][ ssLi = 0,31 2,69 1,70 1,30 163
Be 4
22
4
21][ ssBe = 0,31 3,69 2,05 1,95 109
B 5
122
5
221][ pssB = 0,31 4,69 2,40 2,60 82
C 6
222
6
221][ pssC = 0,31 5,69 2,75 3,25 65
N 7
322
7
221][ pssN = 0,31 6,69 3,10 3,90 54
O 8
422
8
221][ pssO = 0,31 7,69 3,45 4,55 47
F 9
522
9
221][ pssF = 0,31 8,69 3,8 5,20 41
Ne 10
622
10
221][ pssNe = 0,31 9,69 4,15 5,85 36

- 5 -
D Evolution du rayon atomique avec Z
On remarque que le rayon atomique diminue quand Z augmente sur une période (ici 2
ème
période n = 2), car n* est le même mais Z* augmente.
Evolution du rayon atomique avec Z
0
50
100
150
200
2 3 4 5 6 7 8 9 10 11
Numéro atomique Z
Rayon atomique r (pm)
Li
Be
B
CNOFNe