04/10/00 1ère S - cours

TS Déc2014
Devoir de physique-chimie n°3 (1H)
LES EXERCICES SONT INDEPENDANTS – CALCULATRICE AUTORISEE
PHYSIQUE : LES CARACTERISTIQUES ET PROPRIETES DES ONDES /20
Exercice A : La houle /13
La houle est un train de vagues régulier généré par un vent soufflant sur une grande étendue de mer sans obstacle
(étendue appelée le fetch). En arrivant près du rivage, sous certaines conditions, la houle déferle au grand bonheur des
surfeurs !
Les documents utiles à la résolution sont rassemblés en ANNEXE.
Donnée : intensité de la pesanteur : g = 9,8 m.s–2.
A.1. La houle, onde mécanique progressive
A.1.1. Pourquoi peut-on dire que la houle est une onde mécanique progressive ?
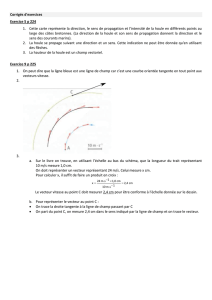
A.1.2. Il est possible de simuler la houle au laboratoire de physique avec une cuve à ondes en utilisant une lame
vibrante qui crée à la surface de l’eau une onde progressive sinusoïdale de fréquence f = 23 Hz. On réalise une
photographie du phénomène observé (cf. document 1 en ANNEXE).
Déterminer, en expliquant la méthode utilisée, la vitesse de propagation vlabo de l’onde sinusoïdale générée
par le vibreur.
A.1.3. Au large de la pointe bretonne, à une profondeur de 3000 m, la houle s’est formée avec une longueur d’onde de 60 m.
En utilisant le document 2 en ANNEXE, calculer la vitesse de propagation v1 de cette houle. En déduire sa
période T.
A.1.4. Arrivée de la houle dans une baie.
A.1.4.1. Sur la photographie aérienne du document 3 en ANNEXE, quel phénomène peut-on observer ? Quelle est la
condition nécessaire à son apparition ?
A.1.4.2. Citer un autre type d’onde pour laquelle on peut observer le même phénomène.
A.2. Projets d'aménagements
Dans la baie photographiée en document 3, un promoteur désire installer un port de plaisance quasi fermé dont l'endroit
est noté sur le schéma. Il serait souhaitable que l'entrée de ce port soit le moins possible soumis à la houle. Deux projets
d'aménagements sont envisagés.
Projet n°1 : on garde un seul chenal (cf. document 4 en ANNEXE)
Projet n° 2 : on refait les digues et 2 chenaux sont créés (cf. document 5 en ANNEXE)
A.2.1 Projet n°1 : Pour que l'entrée du futur port soit peu soumise à la houle, faudrait-il élargir le chenal ou au contraire
le rétrécir ? Justifier soigneusement en vous aidant d’un schéma si nécessaire.
A.2.2. Projet n°2 :
A.2.2.1. Dans le cas du projet n°2, quel nouveau phénomène va faire son apparition dans la baie ? Le décrire en
quelques mots.
A.2.2.2. Si la houle a une longueur d'onde de 34 m, l'entrée du futur port est–elle soumise à une forte houle ou à une
mer calme ?
Même question si la longueur d'onde de la houle est de 80 m ?
A.3. Surfer sur la vague …
Pour la pratique du surf, la configuration optimale est :
- à marée montante c'est-à-dire entre le moment de basse mer (marée basse) et celui de pleine mer (masse haute) ;
- avec une direction du vent venant du Sud-Ouest.
Un surfeur consulte au préalable un site internet qui lui donne toutes les prévisions concernant le vent, la houle et les
horaires des marées (cf. document 6 en ANNEXE).
Proposer en justifiant, un créneau favorable à la pratique du surf entre le jeudi 21 et le samedi 23 juin 2012.
Nom:.......………..................………………….…

figure 1
figure 2
Exercice B : Les fentes d'Young /7
On réalise une expérience (cf. figure 1) à l'aide d'un laser émettant une lumière monochromatique de longueur d'onde .
À quelques centimètres du laser, on place deux fentes distantes d'une distance b. On désigne par a la largeur d'une fente.
Une figure (cf. figure 2) est observée sur un écran blanc situé à une distance D = 3,00 0,03 m des fentes.
Données : a = 100 5 µm ; b = 0,40 0,01 mm
Si on a la formule x = f.g
h alors l'incertitude U(x) = x. 
U(f)
f 2+ 
U(g)
g 2+ 
U(h)
h 2
B.1. Les ondes lumineuses issues de F1 et F2 sont-elles cohérentes ? Justifier.
B.2. Quelle est la relation reliant la distance entre 2 zones d'ombres consécutives (l'interfrange) i et d'autres paramètres
donnés dans l'énoncé ?
B.3. La largeur sur l’écran entre le centre d'une première frange lumineuse et le centre de la septième frange lumineuse
consécutive est de 25 mm (cf. fig. 2 non à l'échelle)
Calculer l'interfrange i.
On admet pour la suite que l'incertitude relative de i est de 1,0 %.
B.4. Pourquoi mesurer plusieurs interfranges au lieu d'une seule ?
B.5. Calculer la longueur d'onde en nm du laser utilisée d'après la mesure effectuée.
B.6. Calculer l'incertitude sur la mesure de la longueur d'onde et écrire la valeur de la longueur d'onde en tenant compte
de l'incertitude.
b

Entrée du
futur port
digue
digue
chenal 1
chenal 2
d1= 1,200 km
m
d2 = 1,880 km
digue
chenal
digue
digue
chenal
Entrée du
futur port
digue
digue
ANNEXE Exercice 1
Document 1 : Simulation de la houle au laboratoire avec une cuve à ondes.
Document 2 : Vitesse de propagation des ondes à la surface de l’eau. D’après http://ifremer.fr/
cas des ondes dites "courtes" (en eau profonde) :
longueur d’onde λ faible devant la profondeur h
de l’océan (λ < h
2 ) v = g.
2
cas des ondes dites "longues" (eau peu profonde) :
longueur d’onde λ très grande devant la profondeur
h de l’océan (λ > 10.h) v = g.h
Document 3 : Photographie aérienne de l’arrivée de
la houle dans une baie.
Document 4 : Projet n°1
Document 5 : Projet n°2
Document 6 : Prévisions maritimes. D’après http://www.windguru.cz/fr/
Tableau des marées – Juin 2012
Jour
Pleine mer
(h :min)
Basse mer
(h :min)
Jeudi 21 juin
06 :54 19 :08
00 :58 13 :10
Vendredi 22 juin
07 :31 19 :44
01 :34 13 :46
Samedi 23 juin
08 :08 20 :22
02 :10 14 :24
Dimanche 24 juin
08 :47 21 :02
02 :49 15 :04

9
chenal
Entrée du
futur port
digue
digue
Correction Devoir de physique-chimie n°3
Exercice A : La houle /1,5+2+1,5+1,5+0,5+1,5+1,5+1,5+1,5 = 13
A.1.1. Une onde mécanique progressive est la propagation d'une perturbation locale de matière sans transport global de matière mais
avec un transport d'énergie. La houle correspond parfaitement à cette définition : la perturbation est la montée et la descente de
la surface de l'eau mais il n'y a pas de transport global d'eau avec la propagation de la houle.
A.1.2. Sur le schéma 14 cm correspond à 6,4 cm et 9 correspond à 5,9 cm.
Ainsi 9 = 14 x 5,9
6,4 donc  = 14 x 5,9 9 x 6,4 = 1,4 cm
vlabo = 
T = .f = 1,4.10–2 x 23 = 0,32 m.s–1
A.1.3.  = 60 m et h = 3000 m donc  << h. D'après le doc 2, v1 = g.
2 = 9,8 x 60 2 = 9,7 m.s–1 Or v1 = 
T donc T =  v1
= 60
9,7 = 6,2 s
A.1.4.1. On observe sur la photographie le phénomène de diffraction. Ce
phénomène apparait de façon très claire si l'ouverture (ici la largeur du
chenal) a une dimension proche de la longueur d'onde de la houle.
A.1.4.2. On peut observer de la diffraction avec des ondes lumineuses (ou
électromagnétiques) (expérience avec un laser et des fils calibrés pour
déterminer l'épaisseur d'un cheveu) ou avec des ondes sonores
(diffraction à la sortie des hauts–parleurs).
A.2.1. Pour que l'entrée du port soit peu soumise à la houle, il faudrait diminuer
l'angle de diffraction  = 
a (avec a largeur du chenal). Pour que  diminue,
il faudrait donc que "a" soit plus grand. Il faut donc élargir le chenal.
A.2.2.1. Avec 2 chenaux, le nouveau phénomène qui va apparaitre est un phénomène d'interférences. Il correspond à une addition de 2
ondes qui se sont diffractées par les 2 ouvertures qui sont les chenaux. Il apparaitra alors, suivant les endroits, des
interférences constructives (des ondes en phase s'additionnent) formant des ondes d'amplitude plus importante et des
interférences destructives (des ondes en opposition de phase s'additionnent) formant des zones d'amplitudes nulles. La
distance, constante, entre les différentes zones d'amplitude nulle est appelée "interfrange".
A.2.2.2. On cherche si la différence de marche  = d2 – d1 est égale à k. avec k  (interférences constructives) ou égale à (k + 1
2).
(interférences destructives) ou ni l'un ni l'autre. On calcule alors 
 = d2 – d1  dans les 2 cas.
Cas où  = 34 m : 
 = 1,880.103 – 1,200.103
34 = 20 = k ainsi les interférences sont constructives : l'entrée du port sera soumis à
une houle d'amplitude forte.
Cas où  = 80 m : 
 = 1,880.103 – 1,200.103
80 = 8,5 = k + 1 2 ainsi les interférences sont destructives : l'entrée du port sera soumis
à une houle d'amplitude quasi nulle.
A.3. Les conditions sont :
 Direction SO du vent
(cf ci–contre : )
 Le jeudi 21, les plages de marée montante sont [00:58 – 06:54] et [13:10 – 19:08] mais la 1ère plage est située en pleine nuit.
Le samedi 23, les plages de marée montante sont [02:10 – 08:08] et [14:24 – 20:22] mais la 1ère plage est en partie la nuit.
Les meilleurs périodes sont donc le jeudi 21 de 14h à 17 h environ (mais le vent, assez fort, est plutôt Ouest–Sud–Ouest) et le
samedi 23 de 15h à 20 h (mais le vent est plus faible)  la meilleure période est le samedi 23 de 15h à 20 h.
Exercice B : Les fentes d'Young /0,5+1,5+1+0,5+1,5+2=7
B.1. Les ondes issues de F1 et de F2 sont issues du même laser (donc de la même onde) qui vient frapper les fentes F1 et F2 en même
temps. Les ondes issues de F1 et de F2 sont donc cohérentes : elles ont les mêmes caractéristiques (f,  et amplitude) et émises
en même temps (en phase).
B.2. i = .D
b ATTENTION : ne pas confondre ici a (largeur des fentes) et b (écartement entre les fentes)
B.3. La distance reliant le centre de 1ère frange au centre de la 7ème frange correspond à 6i. Ainsi 6i = 25 mm donc i = 25
6 = 4,2 mm.
B.4. Il est nécessaire de mesurer plusieurs interfranges pour diminuer l'incertitude de mesure (les erreurs de mesures).
B.5. i = .D
b donc  = i.b D = 4,2.10–3 x 0,40.10–3 3,0 = 5,6.10–7 m = 5,6.102 nm
B.6. U() = .
U(i)
i
2
+ 
U(b)
b
2
+ 
U(D)
D
2
= 5,6.102 x 0,012 + 
0,01
0,40
2
+ 
0,03
3,00
2 car incertitude relative de i : U(i)
i =1 % = 0,01
U() = 2.101 nm = 0,2.102 nm donc  = (5,6  0,2).102 nm