Dossier Samare Olympiade

XVII
èmes
Olympiades de Physique France
Étude de la chute de la graine ailée
d’érable.
Thomas BASILIEN, Antoine CRIBELLIER, Aventin DUPONT
Lycée POTHIER -

2
Sommaire
1. À la recherche d'un échantillon caractéristique pour des expériences
reproductibles 3
1.1. Une présélection visuelle
1.2. Étude du rapport masse graine/masse aile
1.3. Etude du rapport masse de la samare/aire aile
2.Ça tourne autour de quoi? 5
2.1 . Observation
2.2 . Que dit le physicien de la statique? Le centre de gravité
2.3. Que dit le physicien de la dynamique? Le centre d'inertie
2.4 . Que dit le mathématicien ? le barycentre des masses
2.5 . Conclusion.
3.Ça tombe comment verticalement ? 7
3.1. L'expérience
3.2. Bilan des forces
3.3. Etude de la chute verticale
4. Pourquoi ça tourne ? 9
4.1. Les conditions de mise en rotation d’un solide
4.2. La portance de l’aile de la samare
4.3. La vitesse de rotation de la samare lors de sa chute
5. Qu’est-ce qui influe sur les vitesses ? 12
5.1. Cinq Prototypes de samare
5.2. Etude de la vitesse limite acquisse par les différents prototypes
5.3. Etude des vitesses angulaires
5.4. Etudes des inclinaisons des ailes lors de la chute avec rotation.
Conclusion 14

3
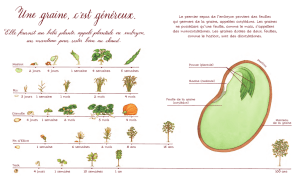
La samare double d'érable est un ensemble de deux akènes munis d'une aile
membraneuse dissymétrique et qui a pour fonction l'anémochorie.
L'observation de la chute d’une samare double montre que les graines tombent en
tourbillonnant à la manière des pales du rotor d’un hélicoptère.
Notre étude porte sur la chute d'une demi samare double, faite à partir de vidéos
réalisées de profil et de dessus. Les questions que nous nous sommes posées sont :
1. ça tourne autour de quoi ?
2. ça tombe comment ? Et pourquoi ?
3. Quels sont les facteurs qui agissent sur les vitesses ?
1. À la recherche d'un échantillon caractéristique pour des expériences
reproductibles
Si on observe bien une similitude entre les mouvements de chute de différentes
samares, il n’en demeure pas moins qu’il existe quelques différences apparentes dues
notamment à la morphologie de la samare (taille de l’aile, planéité de l’aile, état de la
graine…). Il fallait donc travailler sur un échantillon de samares à propriétés physiques
semblables pour pouvoir tirer des lois générales du mouvement de chute.
1.1. Une présélection visuelle
Nous avons présélectionné de grandes samares (envergure ≥ 5 cm), planes et avec
une graine ronde.
Ainsi, pour l’échantillon de 30 samares sélectionnées, on relève les caractéristiques
suivantes :
Masse
moyenne de la
samare (g)
Masse
moyenne de la
graine (g)
Masse
moyenne de
l’aile (g)
Aire moyenne
de l’aile (cm
2
) Aire moyenne de la graine
(cm
2
)
0,22 ± 0,03 0,17 ± 0,03 0,06 ± 0,01 8,06 ± 0,36 0,79 ± 0,05

4
1.2. Étude du rapport masse graine/masse aile
On constate que, pour notre échantillon,
• la masse de l’aile est sensiblement
constante, seule la masse de la
graine varie.
• la masse de l’aile ne représente, le
plus souvent que ¼ environ de la
masse de la samare.
0
0,05
0,1
0,15
0,2
0,25
0 5 10 15 20 25 30
Masse graine (g) Masse aile (g)
1.3. Etude du rapport masse de la samare/aire aile
Hypothèse : Pour disséminer les graines en douceur loin de l’arbre, nous avons pensé que
la nature se « débrouille » pour que la portance liée à l’aire de l’aile soit d’autant plus
grande que la masse est plus importante. Autrement dit, le rapport masse/aire devrait être
à peu près le même pour toutes les « supers samares » sélectionnées.
Rapport masse de la samare sur aire de l'aile
moyenne : 0,028 g.cm
-2
0,000
0,005
0,010
0,015
0,020
0,025
0,030
0,035
0,040
0 5 10 15 20 25 30 35
Pour l’échantillon choisi, 50% seulement des samares à un rapport masse/aire constant et
égal à 0.028g.cm
-2
à 5% près.
Notre hypothèse n’est pas validée. Finalement, la nature diversifie ses chances de
réussite !
G

5
2.Ça tourne autour de quoi?
2.1. Observation
On remarque, lors de la chute vue du dessus de la samare que l'aile et la graine
pivotent autour d'un axe, qui en absence de courant d’air, semble vertical.
2.2. Que dit le physicien de la statique ? Le centre de gravité.
On pose la samare en équilibre horizontal sur une
aiguille. Le point d’équilibre est le centre de gravité.
Deux forces s’exercent : le poids et la réaction de la
pointe.
1
ère
loi de newton
ste
G
CVF =⇔=
∑
0
r
r
Limite de la méthode : la pointe a une épaisseur
déterminant une zone d’équilibre et non un point.
2.3. Que dit le physicien de la dynamique ? Le centre d'inertie.
On fait une vidéo de la chute de la samare vue du dessus. A l’aide d’un logiciel de
pointage et d’exploitation (Regavi + Regressi), on constate qu’un point à un mouvement
plus simple que les autres. C’est le centre d’inertie.
Le centre d’inertie est proche de la jonction de la graine et de l’aile
La détermination précise du centre d’inertie est difficile pour plusieurs raisons :
• la rotation de la samare n’est pas systématiquement dans l'axe de l'objectif,
• le nombre d'images par seconde est insuffisant avec l’appareil photo utilisé.
• le pointage est imprécis sous regavi (images plus ou moins floues).
samare
P
r
R
r
G