TP 1 : Fractales en Python. Complexes / réels, Itératif

T.P. 1 : Fractales en Python.
Complexes / r´eels,
It´eratif / R´ecursif.
Introduction
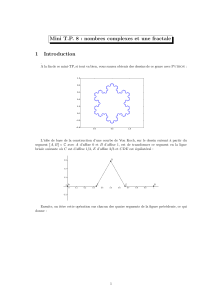
A la fin de ce T.P., si tout va bien, vous saurez obtenir des dessins de ce genre avec Python :
Mais qu’importe le tr´esor, flocon ou chou, l’essentiel est la quˆete. Les vrais buts de ce T.P. sont en
fait les suivants :
●Rafraˆıchir vos connaissance sur la gestion des tableaux numpy qui peuvent ensuite ˆetre
affich´es via matplotlib.pyplot. Pour ceux et celles qui ont fait du SciLab, le gros module
pylab est un module python qui simplifie beaucoup l’utilisation de Python `a la mani`ere
de SciLab en incluant directement aussi bien les fonctions de numpy que de matplotlib.
●Comparer les points de vue : utilisation des transformations complexes ou des matrices 2×2
pour la gestion d’op´erations g´eom´etriques dans le plan.
●Comparer les points de vue : algorithme it´eratif (boucles vues en premi`eres ann´ees) et
algorithme r´ecursif : notion qui n’´etait pas au programme d’I.P.T. en premi`ere ann´ee, et
que nous reprendrons en cours.
1 La courbe de Von Koch, en coordonn´ees complexes, et en
it´eratif
1.1 Construction math´ematique de la courbe de Von Koch
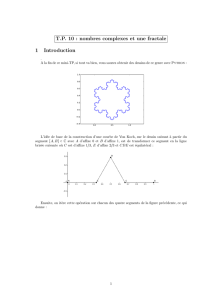
L’id´ee de base de la construction d’une courbe de Von Koch, sur le dessin suivant `a partir du
segment [A, B]⊂Cavec Ad’affixe 0 et Bd’affixe 1, est de transformer ce segment en la ligne
bris´ee suivante o`u Cest d’affixe 1/3, Ed’affixe 2/3 et CDE est ´equilat´eral :
1

Ensuite, on it`ere cette op´eration sur chacun des quatre segments de la figure pr´ec´edente, ce qui
donne :
On peut alors recommencer autant de fois qu’on veut, par exemple apr`es cinq it´erations :
1.2 Rappels de Python avec pylab
Dans toute la suite, nous consid´erons que nous avons rentr´e la commande :
2

import pylab as pl
Le gros module pylab contient numpy, matplotlib (mais pas scipy).
N´eanmoins, `a cause de l’importance de numpy en lui-mˆeme et pour respecter les habitudes,
on importera aussi numpy via import numpy as np pour invoquer les fonctions numpy avec
le pr´efixe np.
1.2.1 Comment manipuler des nombres complexes en Python ?
Il y a au moins deux fa¸cons de rentrer un nombre complexe en Python :
>>>z=1+2j
>>>z=complex(1,2)
En pratique l’entr´ee sous forme a+bj n’est pas tr`es commode (syntaxe p´enible : coller la partie
imaginaire `a j ...), et on recommande plutˆot la commande complex.
Pour un nombre complexe z, avec z.real et z.imag on aura ce que vous pensez.
Remarque : Le help(complex) ne vous renseignera que si vous savez d´ej`a des choses sur les
classes en Python... nous en reparlerons.
1.2.2 Comment afficher des points reli´es par des segments ? plot, exemple :
Pour tracer des points reli´es par des segments, on va utiliser la commande pl.plot, `a laquelle
on doit donner `a manger deux tableaux : l’un sera la liste des abscisses des points successifs, l’autre
celle des ordonn´ees des points successifs. Voici un :
Exemple tr`es simple : trac´e du segment [A, B]o`u A=(1,2)et B=(3,4).
X=[1,3]
Y=[2,4]
pl.plot(X,Y,color="blue") # color est un argument optionnel...
pl.show() # provoque l’affichage si vous ^etes chanceux
pl.savefig(’Desktop/segment.pdf’) # enregistre dans un pdf. : marche mieux
Quelques fonctions graphiques utiles :
pl.axis(’equal’) # pour travailler en rep`ere orthonorm´e
pl.clf() # pour effacer la figure courante.
1.2.3 Les tableaux qu’on peut donner `a manger `a plot
Outre les listes du Python de base, plot g`ere les array de numpy. Ces array sont g´er´es par
l’importation de pylab donc on peut taper :
X=pl.array([1,3])
Y=pl.array([2,4])
pl.plot(X,Y)
On peut aussi, si on a l’habitude d’importer numpy faire import numpy as np et d´eclarer des
np.array.
L’avantage des tableaux numpy,pl.array ou np.array comme on veut, vient des op´erations
qu’on peut faire sur ces tableaux : on peut appliquer des fonctions math´ematiques (fonctions
numpy) `a un tableau numpy.
Un np.array peut ˆetre r´eduit `a une ligne comme A=np.array([1,2]) Il peut ˆetre form´e de plu-
sieurs lignes comme M=np.array([[1,2],[3,4]]) On obtient un joli affichage avec print(A) et
print(M).
3

1.2.4 Trac´e `a partir d’un tableau de nombres complexes
On reprend l’exemple du 1.2.2 o`u cette fois on a stock´e Aet Bdans un tableau contenant deux
complexes.
A=complex(1,2)
B=complex(3,4)
L=np.array([A,B])
Cette fois pour faire le mˆeme trac´e, nous devons d’abord fabriquer des tableaux d’abscisses et
d’ordonn´ees et l`a, on voit la puissance de numpy.
X=np.real(L)
Y=np.imag(L)
pl.clf() # clf pour clearfigure
pl.plot(X,Y)
pl.savefig(’Desktop/segment2.pdf’)
1.3 A vous de jouer !
1.3.1 Fonction transformant un segment
Ecrire une fonction TSC (pour Transformation Segment Complexe), qui prend en argument
deux complexes A et B, et renvoie la liste form´ee des complexes A,C,D,E de la construction de la
courbe de Von Koch donn´ee au §1.1.
Indications :
●Les coordonn´ees complexes de C, D, E sont relatives `a celles de Aet B.
●Une m´ethode simple, qui fait l’int´erˆet des nombres complexes, est de consid´erer que le segment
[C,D] s’obtient par rotation d’angle π/3 (utiliser np.pi), qui se code bien en complexes.
●On pourra v´erifier le r´esultat en le plottant comme indiqu´e dans les paragraphes pr´ec´edents.
1.3.2 Fonction donnant une transformation globale
Ecrire une fonction TGC (pour Transformation Globale Complexe) qui prend en argument une
liste Lde nombres complexes et qui retourne une liste qu’on appellera LT dans la fonction, qui
est la liste obtenue `a partir de Len intercalant entre deux nombres successifs A,B de la liste, les
nombres C,D,E de la construction de Von Koch.
1.3.3 Fonction d’affichage avec choix du nombre d’it´erations
Ecrire une fonction VonKochIC (pour Von Koch par It´eration en coordonn´ees Complexes) qui
prend comme argument obligatoire un entier net comme argument facultatif une liste Lde nombres
complexes, avec la valeur par d´efaut L=[0,1] et qui affiche la courbe de Von Koch obtenue en n
it´erations `a partir du segment Lgrˆace `a la fonction TGC pr´ec´edente.
1.4 Passage de la courbe de Von Koch au triangle de Von Koch
En appliquant la fonction VonKochIC pr´ec´edente aux trois cˆot´es d’un triangle ´equilat´eral, obtenir
le flocon de neige de l’introduction.
2 Le mˆeme travail avec des coordonn´ees r´eelles
2.1 M´emo : La multiplication matricielle avec numpy
En numpy, pour coder la matrice Rde la rotation vectorielle d’angle α, on donne :
R=np.array([[np.cos(alpha),-np.sin(alpha)],[np.sin(alpha),np.cos(alpha)]])
4

Une fa¸con de faire la multiplication matricielle M.N, si Met Nsont des np.array de taille
compatible :
np.dot(M,N)
Attention : Ne pas faire M∗N.
Cette fois, les points Aet Bde d´epart seront cod´es par des matrices colonnes 2 ×1 autrement
dit, par exemple :
A=np.array([[0],[0]])
2.2 A vous de jouer :
2.2.1 Mˆeme d´epart
Ecrire une fonction TSR (pour Transformation Segment R´eelle) faisant la mˆeme chose que TSC
mais en coordonn´ees r´eelles et de mˆeme une fonction TGR analogue `a TGC.
2.2.2 Une petite gymnastique suppl´ementaire n´ecessaire pour l’affichage
Ecrire une fonction Affichage qui prend en argument une liste L=[A1,...,An] dont les
´el´ements Ai sont chacun des np.array repr´esentant des vecteurs colonnes 2×1 et affiche (´eventuellement
dans un fichier pdf) la ligne bris´ee [A1, A2]∪ ⋅ ⋅ ⋅ ∪ [An−1, An].
2.2.3 Mˆeme fin
Ecrire alors une fonction VonKochIR avec les mˆemes sp´ecifications que VonKochIC sauf que la
liste par d´efaut est une liste de points de R2.
3 Le point de vue r´ecursif sur Von Koch r´eel :
def KochRec(n,A=np.array([[0],[0]]),B=np.array([[1],[0]])):
alpha=np.pi/3
R=np.array([[np.cos(alpha),-np.sin(alpha)],
[np.sin(alpha),np.cos(alpha)]])
if n==0:
pl.plot([A[0],B[0]],[A[1],B[1]])
pl.axis(’equal’)
pl.savefig(’Desktop/essai-VonKoch.pdf’)
else :
Ecart=(B-A)/3
C=A+Ecart
E=B-Ecart
D=C+np.dot(R,Ecart)
KochRec(n-1,A,C)
KochRec(n-1,C,D)
KochRec(n-1,D,E)
KochRec(n-1,E,B)
Que fait ce code ? ex´ecutez-le et appelez cette fonction avec de petites valeurs de n.
Que pensez vous du r´esultat ?
5