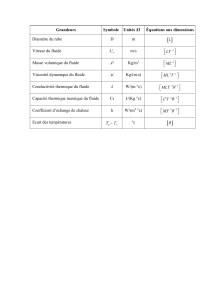
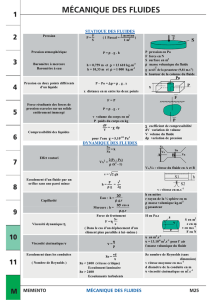
Ondes de gravité de surface ou vagues – Instabilité

1
Ondes de gravité de surface ou vagues – Instabilité de
Rayleigh-Taylor
Introduction
En mécanique des fluides, on désigne par onde de gravité une onde se déplaçant sur la
surface libre d'un liquide soumis à la gravité. Les vagues en milieu ouvert ou le
ballottement
1
en milieu fermé constituent des exemples communs d'ondes de gravité.
Ondes concentriques (vagues) sur un plan d'eau.
En météorologie, on désigne par onde de gravité les variations de pression atmosphérique
créées par la chute d'une masse d'air dense (par exemple en raison du relief du terrain).
Ces ondes sont l'équivalent des vagues dans un milieu en trois dimensions. Elles peuvent
mener à la création de bandes nuageuses parallèles, correspondant aux minima et maxima
de pression (crêtes de l'onde), par exemple dans les cirrus vertebratus
2
.
Patron nuageux formé par les ondes de gravité en aval de l'Île Amsterdam,
une île volcanique de l'Océan Indien.
1
Le ballottement d'un liquide désigne les petits mouvements d'un liquide dans un réservoir, soumis à la
gravité, et en présence d'une surface libre.
2
Les cirrus vertebratus sont des nuages disposés en bandes alternées et parallèles, rappelant des vertèbres
ou des arrêtes de poisson. Une telle organisation spatiale suggère que le système nuageux a été généré par
la présence d'ondes de gravité.

2
Il ne faut pas confondre (mais selon les auteurs les deux terminologies sont employées)
« onde de gravité » et « onde gravitationnelle » cette dernière expression faisant plutôt
référence à la propagation d’une perturbation de courbure de l’espace temps en relativité
générale.
Dans le cas des ondes de gravité, essentiellement, un fluide léger tombe sur un fluide plus
lourd. Dans le cas contraire (fluide lourd tombant sur un fluide léger) la situation est
instable, ne possède pas de solution de type onde, et donne lieu à l’instabilité dite de
Rayleigh-Taylor.
Prenez deux fluides, un lourd et un léger, superposés dans un champ de gravitation (voir
figure).
Conditions initiales de l’instabilité de Rayleigh-Taylor
Ce système est instable. En effet, échangeons par la pensée un volume de fluide léger,
situé près de l'interface entre les deux fluides, avec un même volume de fluide lourd de
l'autre côté de cette interface. L'énergie potentielle de gravitation du système a diminué
tout comme son énergie totale. C'est la tendance naturelle de ce système à minimiser son
énergie potentielle de gravitation qui crée l'instabilité. Bien sûr, cette perte d'énergie est
compensée par l'augmentation d'une autre forme d'énergie : l'énergie cinétique. En bref,
le fluide lourd va passer sous le léger (et le léger sur le lourd, par symétrie), et ce
mouvement s'accompagne forcément d'une création d'énergie cinétique. Dans le cas des
vagues, si le fluide léger supérieur s’engouffre dans le fluide lourd inférieur, la poussée
d’Archimède tend à ramener le fluide léger à sa position initiale : il y a donc au contraire
stabilité et propagation d’ondes à l’interface. La figure suivante montre le résultat d'une
simulation numérique bidimensionnelle de l’évolution de l’instabilité de Rayleigh-Taylor,
avec une interface initiale légèrement et aléatoirement perturbée.

3
Le fluide lourd tombe, le fluide léger monte. Les deux fluides se croisent avec une
géométrie souvent qualifiée de champignons ou de doigts de Rayleigh-Taylor par les
chercheurs. Une simulation tridimensionnelle comme sur la figure ci-dessous, est bien
évidemment plus réaliste que la simulation bidimensionnelle et montre des champignons
un peu différents sans pour autant changer radicalement l'aspect global de la géométrie de
l'instabilité.
Instabilité de Rayleigh-Taylor : simulation 3D (Los Alamos National Institute)
On observe aussi des instabilités de Rayleigh-Taylor (on parle alors de « doigts de sel »)
lorsqu’un fleuve se jette dans la mer : la mer est le fluide dense salé qui est accéléré par le
fluide moins dense non salé du fleuve. Le fluide salé de la mer pénètre l’eau douce du
fleuve avec une géométrie typique de l’instabilité de Rayleigh-Taylor.
En astrophysique, l’instabilité de Rayleigh-Taylor s’observe aussi très souvent.

4
Nébuleuse planétaire Hélix (clichés de O’Dell, Hubble Space Telescope) : un vent
stellaire central rapide et peu dense entre en collision avec un vent stellaire plus dense et
moins rapide; il y a génération de doigts de Rayleigh-Taylor à l’interface.
Ci-dessous, on peut voir une simulation hydrodynamique que j’ai réalisée en 1999 dans le
cadre de mon doctorat. On y calcule l’évolution d’un globule de un rayon solaire, en
équilibre de pression dans un vent stellaire allant à
-1
1000 km s
. Le but était d’étudier la
survie d'une inhomogénéité sphérique composée d'hydrogène et de rayon 1 rayon solaire,
située à proximité d’une étoile à vent stellaire rapide. La densité du globule est 50 fois
plus grande que celle du vent ambiant. Afin d'assurer une relative survie du globule, il
convient de limiter son expansion due à la pression. Sa température a donc été choisie 50
fois plus petite que celle du vent ambiant (50000 K), soit 1000 K. Ainsi la pression du
globule est égale à celle du vent local. Pour satisfaire la condition d'anti corrélation de la
densité avec la vitesse des surdensités des vents stellaires compressibles (cf. complément
de cours sur la compressibilité, sous section Contrastes de densité et nombre de Mach ), le
globule a été choisi plus lent que le vent ambiant avec une vitesse de dérive relative
s'élevant à 100 km/s, le vent ayant de son côté une vitesse terminale de 1000 km/s et un
taux de perte de masse de 10-6 masses solaires par an. Les calculs ont été menés en
coordonnées cylindriques ( z , r , ϕ ), en supposant une symétrie de rotation relativement à
l'axe du cylindre z , rendant les simulations bidimensionnelles dans le plan ( z , r ). Les
calculs prennent en compte le refroidissement collisionnel du gaz. La grille de calcul est
constituée de 400 x 100 zones équidistantes en z et r , respectivement, sur les intervalles
spatiaux 8 R* ≤ z ≤ 16 R*, et 0 ≤ r ≤ 2 R*, avec R* = 1 rayon solaire, le centre du globule
se trouvant initialement à 10 rayons solaires de la surface de l'étoile. La figure montre les
résultats d'une telle simulation purement hydrodynamique : un globule sphérique, froid et
lent, dont le rayon vaut 1 rayon solaire et dont la densité est 50 fois plus importante que
celle du vent est significativement affecté par l'instabilité de Rayleigh-Taylor au bout de
~40 heures, et achève sa division au bout de ~50 heures, la vitesse de dérive devenant, de
son côté, nulle.

5
-12.80 -11.15
42h
35h
28h
21h
14h
7h
0h
8R*16R*
z
r
2R
0
*
1000 km/s
vent
900 km/s
log(rho) g/cm^3
Masse du globule : 5,7x10 masses solaires
-12