DST 1

CLASSE DE TERMINALE S
Le : 20 septembre 2006
Durée : 3 h 30
Physique-Chimie
DEVOIR SUR TABLE N° 1
TOUT DOCUMENT INTERDIT.
L’usage de calculatrices scientifiques à mémoire est autorisé.
Les résultats numériques doivent être précédés d’un calcul littéral.
La présentation et la rédaction font partie du sujet et interviennent dans la notation.
L’épreuve est notée sur 16 points auxquels s’ajouteront les points d’épreuve pratique sur 4 points.
I ] CHIMIE : sur 6,5 points. DOSAGES DE L’ACIDE A
DOSAGES DE L’ACIDE ADOSAGES DE L’ACIDE A
DOSAGES DE L’ACIDE ASCORBIQUE
SCORBIQUESCORBIQUE
SCORBIQUE
La vitamine C, ou acide ascorbique, est vendue en pharmacie sous forme de comprimés. La molécule d’acide
ascorbique a pour formule brute C6H8O6 et pour masse molaire moléculaire : MvitC = 176 g.mol-1.
L’acide ascorbique est un monoacide qui appartient à un couple acide / base d’une part, et à une couple oxydant /
réducteur d’autre part. Ce dernier est défini par : acide déshydroascorbique : C6H6O6 / acide ascorbique : C6H8O6.
On désire déterminer la teneur en acide ascorbique d'une solution. On envisage deux méthodes de dosage,
reposant l'une sur le caractère acide de la molécule et, l'autre, sur son caractère réducteur.
1. Dosage acido-basique de la solution d'acide ascorbique.
On réalise un dosage pH-métrique de 10,0 mL de la solution d'acide ascorbique par une solution d'hydroxyde de
sodium, ou soude, de concentration molaire volumique : CB = 5,00.10-4 mol.L-1.
1.1. Écrire l'équation chimique de la réaction de dosage.
1.2. Définir l'équivalence du dosage.
1.3. Le volume de soude versé à l’équivalence est : Véquiv = 9,00 mL.
En déduire la valeur de la concentration molaire volumique de la solution titrée.
2. Dosage par oxydoréduction de la solution d'acide ascorbique.
Il s’effectue en deux étapes par colorimétrie.
 Étape 1 : l'acide ascorbique est oxydé par une solution de diiode I2 en excès, couple : I2aq / I–aq.
On verse dans un erlenmeyer un volume : V1 = 10,0 mL de la solution d'acide ascorbique auquel on ajoute un
volume : V2 = 20,0 mL d'une solution de diiode de concentration molaire volumique : C2 = 1,00 10-3 mol.L-1.
 Étape 2 : dosage du diiode en excès.
Le diiode en excès est alors dosé par une solution de thiosulfate de sodium (2 Na+aq + S2O32–aq et couple :
S4O62–aq / S2O32–aq) de concentration molaire volumique : C3 = 2,40.10-3 mol.L-1, en présence d'empois d'amidon ou de thiodène.
Le volume versé à l'équivalence est : V’équiv = 12,9 mL.
2.1. Préciser la verrerie utilisée pour prélever les volumes des réactifs de la première étape. On justifiera les choix.
2.2. Faire le schéma légendé du dispositif du dosage colorimétrique. Comment repère-t-on son équivalence ?
2.3. Exprimer la quantité de matière initiale de diiode nI2 initial introduite dans la première étape.
2.4. Établir l'équation chimique de la réaction d'oxydoréduction de la première étape.
2.5. Établir l'équation de la réaction d'oxydoréduction de la seconde étape.
2.6. En déduire la quantité de matière de diiode en excès nI2 excès qui réagit avec la solution de thiosulfate de
sodium lors de la seconde étape.
2.7. Établir la relation donnant la quantité de matière d'acide ascorbique dosée.
2.8. En déduire la concentration molaire volumique de la solution d'acide ascorbique.
3. Conclusion.
3.1. Comparer les résultats obtenus par les deux méthodes de dosage. Calculer un pourcentage d’écart et conclure.
3.2. Calculer la concentration massique volumique en acide ascorbique de la solution titrée.
3.3. On envisage de réaliser le dosage acido-basique par conductimétrie de la solution d’acide ascorbique. Tracer
l’allure de la courbe de dosage attendu, donnant la conductivité σ du mélange réactionnel en fonction du
volume VB de la solution de réactif titrant. Justifier le tracé et y faire figurer le point d’équivalence.
On donne : λascorbate = 10,5.10-4 S.m2.mol-1 ; λHO– = 199.10-4 S.m2.mol-1 ; λNa+ = 50,1.10-4 S.m2.mol-1.
II ] PHYSIQUE : sur 4 points. LA HOULE
LA HOULELA HOULE
LA HOULE
On s'intéressera dans cet exercice à l'étude de la houle en haute mer, à savoir en eau profonde, et aux
caractéristiques de celle-ci en fonction d'une échelle en intensité appelée « échelle de Beaufort ».
... / ...

Dans une revue maritime traitant du sujet, on peut lire le texte suivant :
« Lorsque le vent souffle sur une mer calme, le frottement de l'air crée de petites rides puis des vaguelettes et enfin
des vagues, à mesure que la vitesse du vent augmente. L'ensemble de ces vagues, généré sur un intervalle de temps
plus ou moins long, constitue la houle. Cette houle peut être décrite à l'aide de trois paramètres.
La hauteur h, définie comme la distance verticale entre le sommet de la crête et le fond du creux de la vague. La
longueur L, comme la distance entre deux crêtes ou deux creux successifs. La cambrure, définie comme le rapport de sa
hauteur sur sa longueur. ».
Ainsi le phénomène de la houle peut être considéré comme une onde mécanique. Aussi on assimilera dans tout
l'exercice la houle à une onde progressive périodique sinusoïdale rectiligne dont les paramètres caractéristiques peuvent
varier suivant l'état de la mer.
1. 1.1. Le schéma qui suit représente la surface de l'eau affectée par la houle à un instant donné. Reproduire ce
schéma et y noter les paramètres « hauteur » et « longueur ».
1.2. À quelle grandeur spatiale, caractéristique d'un phénomène ondulatoire, est associé le terme « longueur » du
texte d'introduction ? Quelle est sa définition ?
1.3. Quelle grandeur temporelle permet de caractériser une onde mécanique ? Quelle est sa définition ?
2. L'échelle de Beaufort, établie en 1805 – du nom de l'amiral de la marine britannique Francis Beaufort – et graduée
de 0 à 12, permet de caractériser la vitesse des vents. L'état de la mer étant directement lié à la vitesse du vent, cette
échelle permet également de caractériser l'état de la mer et donc les conditions de navigation. Le tableau qui suit
présente les derniers degrés d'une échelle de Beaufort simplifiée que vous utiliserez dans la suite de l'exercice.
Échelle de Beaufort simplifiée
Degré sur l'échelle Hauteur h de la houle (en mètres)
5 2,00
6 3,00
7 4,00
8 5,50
9 7,00
10 9,00
11 11,5
12 14,0
On se place dans le cas où la cambrure des vagues notée Ca est telle que Ca = 1 / 7 = 0,143.
On gardera cette valeur de cambrure pour tout le reste de l'exercice.
2.1. Donner l'expression reliant la hauteur h des vagues, leur longueur L et leur cambrure Ca.
2.2. Déterminer alors la longueur des vagues pour les degrés 6, 8, 10 et 12 de l'échelle de Beaufort.
3. 3.1. Donner l'expression reliant la longueur L de la question 1.1.2., la célérité v de l'onde et sa période T.
3.2. En déduire l'expression reliant la longueur L, la célérité v et la fréquence f de l'onde associée.
3.3. Le tableau fourni ci-dessous donne également les périodes associées aux différents degrés de l'échelle. Pour
les degrés 7 et 10 de l'échelle de Beaufort, déterminer la célérité v de l'onde associée.
Échelle de Beaufort 5 6 7 8 9 10 11 12
Hauteur h de la houle (en m) 2,00 3,00 4,00 5,50 7,00 9,00 11,5 14,0
Longueur L (en m) 14,0 28,0 49,0 80,5
Période T (en s) 2,10 2,60 3,00 3,50 4,00 4,50 5,10 5,60
Célérité v (en m.s-1) 6,67 8,08 11,0 12,3 15,8 17,5
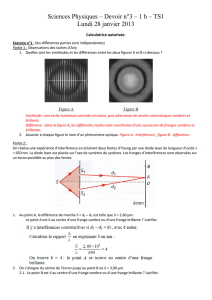
4. On donne ci-après la courbe traduisant l'évolution v2 = f (L).
4.1. Établir l’équation numérique de la fonction : v2 = f (L).
4.2. Ce résultat est-il en accord avec les données du tableau de la question 3.3. ?
5. 5.1. Déterminer l'expression numérique reliant la célérité v de la houle à sa fréquence f.
5.2. Conclure quant à la nature dispersive du milieu de propagation de la houle. Un milieu de propagation est
dispersif lorsque la célérité de la propagation d’une onde est fonction de la fréquence de celle-ci.
.../ p. 3

Terminale S D.S.T. N° 1 Page 3
III ] PHYSIQUE : sur 5,5 points. SUR LES ONDES...
SUR LES ONDES...SUR LES ONDES...
SUR LES ONDES...
1. La tonalité du téléphone.
Le son émis par la tonalité du téléphone est quasi sinusoïdal. Sa fréquence est de 440 Hz, fréquence identique à
celle du son émis par un diapason, le « la 3 ».
1.1. Calculer la période T de cette onde sonore.
1.2. La célérité du son dans l'air sec à 0,00°C et à la pression de 1 013,3 hPa est de v = 331,45 m.s-1. Calculer la
longueur d'onde de l'onde sonore émise par la tonalité du téléphone dans l'air considéré précédemment.
1.3. La célérité du son dans un gaz est proportionnelle à la racine carrée de la température absolue de l'air dans lequel se
propage le son. On considère maintenant un air sec à la température de 27,0°C et à la pression de 1 013 hPa
1.3.1. Calculer la célérité du son sans cet air.
1.3.2. Calculer la nouvelle longueur d'onde de l'onde émise par la tonalité du téléphone.
2. Télémètre.
Un télémètre comporte, dans un même boîtier, un émetteur et un récepteur d'ondes ultrasonores de fréquence 40,0 kHz.
Pour mesurer la distance d où se situe un obstacle, on oriente l'appareil dans sa direction, puis on déclenche
l'émission. Cette-ci est interrompue dès que le récepteur reçoit l'onde réfléchie.
La durée d'émission est déterminée par comptage et affichage du nombre d'impulsions délivrées par un oscillateur
de fréquence f. L'affichage comporte trois digits et clignote en cas de dépassement de la capacité de mesure.
L'étalonnage de l'appareil est réalisé à 20,0°C, pour une célérité de l'onde ultrasonore de 342 m.s-1. Une unité affichée
correspond alors à une distance d de 1,00 cm.
2.1. Quelle distance maximale peut être mesurée par le télémètre ?
2.2. Quelle est, pour cette distance, la durée totale de propagation de l'onde ultrasonore ?
2.3. Quelle doit être la valeur de la fréquence f de l'oscillateur d’impulsion de comptage ?
2.4. La télémètre indique une distance d = 850 cm pour une mesure effectuée alors que la température de l’air est
égale à 10,0°C. La distance réelle est-elle supérieure ou inférieure à cette valeur ?
2.5. Quelle est l'erreur, exprimée en cm, commise sur cette mesure ?
On rappelle que la célérité des ultrasons est proportionnelle à la racine carrée de la température absolue.
3. Corde à linge.
Fabien joue avec la corde à linge tombée sur le sol du jardin. II en saisit une
extrémité qu'il déplace rapidement vers le haut, et qu'il laisse lentement retomber au
sol. Le déplacement de sa main au cours du temps est représenté ci-contre.
Cette corde mesure : L = 10,0 m.
3.1. Quelle est la nature de la perturbation subie par la corde à linge ? Justifier.
3.2. Cette onde est-elle longitudinale ou transversale ? Justifier la réponse.
3.3. Sachant que la perturbation atteint l'autre extrémité de la corde en 1,00 s,
quelle est la célérité v de l'onde ?
3.4. Représenter le mouvement au cours du temps d'un point de la corde situé à
une distance d = 2,00 m de la main de Fabien.
3.5. Représenter la photographie de la corde à l'instant t1 = 100 ms.
Cette représentation est-elle identique à celle demandée à la question 3.4. ?
3.6. Déduire de la question précédente la photographie de la corde à l'instant t2 = t1 + 500 ms.