Module 30 94 Soient les événements : A : test positif, A* : test négatif

Module 30
94
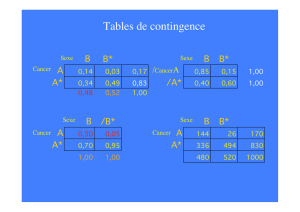
Soient les événements :
A : test positif, A* : test négatif
B : malade, B* : sain
Pour mettre au point et tester les qualités de la méthode de dépistage, des
tests cliniques doivent être réalisés sur des personnes diagnostiquées avec
certitude.
Malade (B)
Sain (B*)
Test+ (A)
99
90
189
Test- (A*)
1
810
811
100
900
1000
Tableau 30-14. Table de contingence établie sur des personnes réellement
malades ou réellement saines (n = 1000) pour une prévalence de 10 %.
Nous constatons dans la table 30-14 que la prévalence de ce cancer dans
cette population est de 100/1000 =0,1.
Malade (B)
Sain (B*)
Test+ (A)
0,099
0,090
0,189
Test- (A*)
0,001
0,810
0,811
0,100
0,900
1,000
Tableau 30-15. Table de probabilité établie sur des personnes réellement
malades ou réellement saines (n = 1000) pour une prévalence de 10 %.
Malade (B)
Sain (B*)
Test+ (A)
0,99
0,1
Test- (A*)
0,01
0,9
1
1
Tableau 30-16. Table de probabilités conditionnelles établie sur des personnes
réellement malades ou réellement saines (n = 1000) pour une prévalence de
10 %.
Dans notre exemple, pour les personnes cancéreuses avec certitude : la
réaction est positive dans 99 % des cas.
P(A/B) = 0,99 (sensibilité) et P(A */B) = 0,01
La sensibilité du test est sa capacité à détecter les vrais positifs. Mais il
est facile de faire un test sensible : il suffit qu’il soit toujours positif ! Il doit donc
aussi être spécifique.

Module 30
95
Sur des personnes diagnostiquées saines avec certitude : le test est
négatif dans 90 % des cas.
P(A */B *) = 0,90 (spécificité) et P(A/B *) = 0,10
La spécificité du test est sa capacité à détecter les vrais négatifs. Il doit
être négatif si la personne est saine.
Nous disposons donc d’un test de détection dont la sensibilité est de
99 % et la spécificité de 90 %, performances établies sur des personnes
dont l’état de santé est connu par des investigations plus poussées.
Lors de l’utilisation du test, par définition l’état de santé n’est pas connu :
les performances du test sur le terrain se nomment le pouvoir prédictif positif et
le pouvoir prédictif négatif. Ceux-ci se calculent sur la table de probabilité
conditionnelle « dans le contexte du test » et dépend dramatiquement de la
prévalence de la maladie.
Malade (B)
Sain (B*)
Test+ (A)
0,524
0,476
1,000
Test- (A*)
0,001
0,999
1,000
Tableau 30-17. Table de probabilités conditionnelles établie sur des personnes
réellement malades ou réellement saines (n = 1000) pour une prévalence de
10 %.
Dans le cas d’une prévalence de 0,1 (fort élevée) le pouvoir prédictif
positif P(B/A) est seulement de 0,524, soit à peu près une chance sur deux, en
recevant le résultat du test, de déclarer malade une personne saine !
Reprenons le raisonnement sur base de la table de contingence
(Tableau 30-14). Une petite erreur (1-spécificité = 10 %) sur un grand
nombre de négatifs (900) produit un grand taux de faux positifs (90). Une
bonne sensibilité (99 %) sur un petit nombre de positifs (100) produit un
petit nombre de vrais positifs (99). En considérant l’ensemble des tests
positifs (189) le pouvoir prédictif positif est de 99/189 = 0,524.
Ce phénomène sera d’autant plus marqué que la prévalence sera faible,
car le nombre de vrais positifs (rares) détectés sera très petit par rapport au
grand nombre de négatifs déclarés positifs par erreur (1-spécificité).