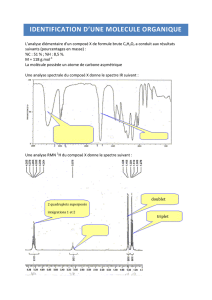
Spectroscopie infra-rouge

-1-
Chimie organique 8 :
Spectroscopie infra-rouge
Jusqu’au début du XXème siècle, l’identification de molécules organiques constituait un lourd travail. Les grosses molécules
étaient d’abord fragmentées au moyen de réactions chimiques. Les propriétés des fragments analysées permettaient
d’identifier les fragments, puis de reconstituer la grosse molécule en « recollant » les fragments. Des tests caractéristiques
pouvaient également conduits pour déterminer les groupes fonctionnels de la molécule.
Aujourd’hui, les tests caractéristiques ont pratiquement disparu. On préfère utiliser des méthodes spectroscopiques
(interaction matière-rayonnement) pour obtenir très rapidement la structure d’une molécule organique. Deux techniques
seront abordées dans le programme de PC :
 Spectroscopie infrarouge → Accès aux groupes fonctionnels
 Spectroscopie RMN 1H → Accès à la structure de la molécule (enchaînement des atomes, …)
1. Interaction matière-rayonnement
1.1. Rayonnement
- Dualité onde-corpuscule :
o Nature ondulatoire : la lumière est décrite comme une onde électromagnétique. Deux vecteurs normaux (champ
magnétique et champ électrique) oscillent dans un plan perpendiculaire à la direction de propagation de l’onde.
Cette onde est dotée d’une double périodicité : spatiale (longueur d’onde λ) et temporelle (période T). Ces deux
périodes sont liées par la relation : λ = cT (avec c : célérité de l’onde).
o Nature corpusculaire : La lumière peut être vue comme un flux de particules matérielle de masse nulle, les photons.
Chaque photon transporte une énergie ε = hν (avec ν : fréquence).
- Synthèse des deux approches par la relation de de Broglie : ε = 
 (avec h : constante de Planck : h = 6,62.10-34 J.s)
- La mécanique quantique montre que les niveaux d’énergie d’une molécule sont discrets. Un photon ne peut être absorbé
que s’il transporte l’énergie hν exactement égale à la différence d’énergie entre deux niveaux de la molécule.

-2-
Monochromateur
Faisceau de
référence (Iincident)
Source de
rayonnements
électromagnétiques
Photo-
détecteur
Échantillon
Faisceau
incident
Faisceau
transmis (Itransmis)
Enregistreur
1.2. Spectroscopie d’absorption
- Spectre : Réaliser un spectre d’absorption consiste à
o Soumettre le milieu à un rayonnement
o Puis comparer, pour chacune des fréquences utilisées, l’intensité du rayonnement à l’entrée (Iincidente) et à la sortie
(Itransmise) de l’échantillon.
- Pour quantifier cette absorption par un échantillon, on utilise un spectromètre d’absorption.
- Grandeurs caractéristiques de la part d’énergie qui a été absorbée :
o Transmittance :   
S’exprime en % : T = 100 % : la totalité du rayonnement est absorbé
T = 0 % : le rayonnement n’est pas du tout absorbé.
o Absorbance :  
Sans unité : A = 0 : le rayonnement n’est pas du tout absorbé
En théorie, si la totalité du rayonnement est absorbé, A tend vers l’infini, mais les appareils
ne sont pas capables de détecter une intensité transmise si faible.
- Grandeurs caractéristiques du rayonnement : La fréquence est exprimée à travers deux grandeurs :
o Longueur d’onde :   
Grandeur inversement proportionnelle à la fréquence : λ grande → énergie faible
Pour le domaine infrarouge, utilisé en spectroscopie organique, 2,5 µm < λ < 16 µm
o Nombre d’onde :   
Grandeur proportionnelle à la fréquence : σ grand → énergie élevée.
Pour le domaine infrarouge utilisé en spectroscopie organique, 600 cm-1 < σ < 4000 cm-1

-3-
- Deux présentations de spectres équivalentes :
A = f(λ) pour la spectroscopie UV-visible : T = f(σ) pour la spectroscopie IR :
- Linéarité de l’absorbance : L’absorbance peut être assimilée à une fonction linéaire de la concentration molaire dans le cas
de solutions suffisamment diluées (typiquement C < 0,1 mol.L-1). D’autre part, l’absorbance est additive.
Pour une seule espèce absorbante : loi de Beer-Lambert s’écrit (noms et unités des termes à connaître) :
A = εℓC
A : absorbance (sans unité)
ε : coefficient d’absorption molaire (en L.mol-1.cm-1)
ℓ : longueur de la cuve (en cm)
C : concentration molaire de l’espèce absorbante (en mol.L-1)
Pour une solution contenant plusieurs espèces absorbantes :
A = 
Remarque : Sur le trajet du rayon lumineux, ne se trouve pas uniquement la molécule étudiée, mais également la cuve et le
solvant, qui absorbent aussi une partie du rayonnement.
Ainsi, l’absorbance globale est en réalité la somme de plusieurs contributions :
Amesurée = Acuve + Asolvant + molécules étudiées
On élimine la composante non pertinente (solvant + cuve) en réalisant le blanc. Ainsi, la valeur affichée par l’appareil est alors :
Aaffichée = Amesurée – Ablanc = molécules étudiées
2. Vibrations d’une molécule
2.1. Energie et vibration
- Les OM sont obtenues par recouvrement des OA. L’énergie d’une OM est directement liée au recouvrement des OA et donc
aux distances entre atomes. L’énergie d’une OM est donc liée à la distance interatomique.
- Par conséquent, toute modification de la géométrie de la molécule (angles ou longueurs des liaisons) modifie son énergie.
Inversement, un apport d’énergie peut modifier la géométrie (distances, angles) d’une molécule = la faire vibrer.

-4-
2.2. Niveaux d’énergie vibrationnels étude d’une molécule A-B
On considère ici une molécule diatomique hétéronucléaire représentée par A-B.
- Energie potentielle du système : résultante de deux termes directement liés à la distance r entre les atomes :
o Un terme d’attraction entre les atomes en -1/r6
o Un terme de répulsion à courte distance entre les noyaux (charges positives se repoussent), en 1/r12.
- La somme de ces deux contributions donne l’énergie potentielle du système A-B en fonction de la distance r :
Longueur de liaison d’équilibre =
distance au minimum d’énergie
- Apports de la mécanique quantique : Toutes les valeurs d’énergie ne
sont pas accessibles. Seule une partie de ces valeurs peut être adoptée
par le système. Il convient donc d’ajouter à la représentation
précédente les différents niveaux accessibles.
Chaque niveau d’énergie est relié au nombre quantique vibrationnel,
noté v (v entier naturel) :
E = (v + ½) hν0 (ν0 : fréquence propre de l’oscillateur)
- Modélisation harmonique : La modélisation la plus simple de cette courbe (notée Morse ci-dessous), consiste à la
remplacer par une parabole. En effet, un changement de variables (x = r – req et E = Ep – Eeq) permet d’exprimer
simplement l’énergie potentielle sous la forme E = ½ kx2.
Le système est alors équivalent à un oscillateur harmonique (avec une force de rappel de norme kx).
o Modélisation de la liaison par un ressort :

-5-
o Système de 2 points matériels étudié dans le référentiel barycentrique → revient à étudier un mobile de masse
réduite µ, accroché à un ressort dont l’autre extrémité est fixe.
µ = 
o Equation différentielle → … → Fréquence d’oscillation propre :
Pulsation propre : 
Fréquence propre d’oscillation : 
 (loi de Hooke)
Analyse de la formule :
Liaison forte → Constante de raideur k grande → Fréquence de vibration ν0 élevée
2.3. Types de vibrations
- Vibration = modification de la géométrie de la molécule
→ Modification des distances interatomiques ou des angles de liaison.
- Deux types de vibrations :
o Vibration d’élongation : les longueurs de liaison oscillent (allongement/raccourcissement/allongement)
o Vibration de déformation : les angles entre liaisons oscillent (augmentation/diminution/augmentation)
- Expl : Modes de vibration de la molécule d’eau (H-O-H) :
Remarque : Les molécules diatomiques (H2, N2, CO, …) ne peuvent avoir de vibration de déformation (pas d’angle entre
liaisons puisqu’il n’y a qu’une seule liaison !).