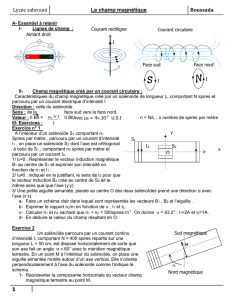
champ magnetique

Chapitre 1 Champs et Interactions Leçon 3 Champ magnétique
Leçon 3. CHAMP MAGNETIQUE
Exercice n° 1 Solénoïdes
1. Soit un premier solénoïde S1 de longueur l = 50 cm et comportant 200 spires.
a) Quel est le champ magnétique B
r
produit au centre de ce solénoïde lorsqu'il est parcouru par
un courant électrique d'intensité I ? Faire un schéma clair en figurant le sens du courant et le sens
du champ magnétique.
Perméabilité du vide.. µ0 = 4π.10-7 S.I.
b) On place une petite aiguille aimantée à l'intérieur de S1 au voisinage de son centre. L’axe de
S1 est disposé horizontalement et perpendiculairement au plan du méridien magnétique.
Calculer l'intensité l du courant qu'il faut faire passer dans S1 pour que l'aiguille aimantée dévie
de 30°.
Composante horizontale du champ magnétique terrestre : BH = 2,0.10-5 T.
2. Soit un second solénoïde S2 comportant 80 spires par mètre de longueur. Les deux solénoïdes
S1 et S2 sont disposés de manière à avoir le même axe, cet axe commun étant perpendiculaire au
méridien magnétique (voir figure).
Les deux solénoïdes sont branchés en
série dans un circuit électrique et on
constate que l'aiguille aimantée dévie de
45°. Déterminer la valeur de l'intensité I’
du courant qui les traverse; on trouvera
deux solutions qui devront être
interprétées.
1. a. Lorsque le solénoïde est parcouru par un courant I, le champ magnétique B
r
au centre du
solénoïde est parallèle à l’axe du solénoïde, son sens dépend du sens du courant et est donné par
la règle de la main droite, ou du bonhomme d’Ampère, et sa valeur est : I
l
N
B0 µ= ( B en
teslas, l en mètres, I en ampères)
I
B
r
1. b. L’aiguille aimantée prend la direction du champ résultant : H
tBBB
r
r
r
+=
elle tourne d’un angle α : tan α =
H
B
B B = BH tan α I
l
N
0
µ = tan α .BH
16

Chapitre 1 Champs et Interactions Leçon 3 Champ magnétique
N
l.Btan
I
0
H
µ
α
= α = 30° ; BH = 2,0.10-5T ; l = 0,50 m ; N = 200 spires I = 23 mA
I
B
r
H
B
r
α
tB
r
2. Les 2 solénoïdes ont le même axe : les champs magnétiques 1
B
r
et 2 B
r
créés par chacun des
solénoïdes sont colinéaires, de même sens ou de sens contraire selon le sens du courant.
Champ résultant : 21 BBB
r
r
r
+=
Même sens du courant dans S1 et dans S2 : B = B1 + B2
Sens contraire : B = |B1 – B2|
1
B
r
2
B
r
1
B
r
2
B
r
L’aiguille tourne d’un angle α : tan α = H
B
B I
l
N
B01 µ= n1 = l
N n
1 = 400 spires/m
B
2 = µ0 n2 I n2 = 80 spires/m
n1 > n2 : le champ résultant a toujours le sens de B1 : B = B1
±
B2
B = µ0 I ( n1± n2 ) B = BH tan α )nn(
tanB
I
210
H
±µ
α
=
Application numérique : )80400(10.4
10.0,245tan
I7
5
±π
×°
=−
−
Pour que l’aiguille tourne de 45° : I'1 = 33 mA si B = B1 + B2 et I'2 = 50 mA si B = B1 – B2
17

Chapitre 1 Champs et Interactions Leçon 3 Champ magnétique
Exercice n°2
-Les figures 1 ,3,4, de l'exercice sont vues du dessus.
Les bobines de Helmholtz sont deux bobines identiques, plates, de même axe, séparées d'une
distance égale à leur rayon et parcourues par des courants de même intensité et de même sens
(figure 1).
On donne la composante horizontale du champ terrestre BH=2,0. 10-5 T
Dans la question 1, le champ terrestre est négligeable
1 a) –Indiquer sur la figure 1 quelques lignes de champ magnétique, dans l'espace situé entre les
bobines et dans le voisinage extérieur immédiat. Orienter les lignes de champ, positionner sur
l'une d'elles une petite aiguille aimantée dont on indiquera les pôles. (On ne demande pas de
justifier)
b) – On fait varier l'intensité I du courant dans les bobines. On mesure la valeur B du champ
magnétique entre les bobines. On obtient le graphe I→ B =f ( I ) ( figure 2 )
-D'après le graphe, quelle est la relation entre B et I , littéralement et numériquement?
2. Dans les questions 2 et 3, le champ terrestre n'est pas négligeable
Figure 3 On place les 2 bobines de Helmholtz dans le plan du méridien magnétique.
En l'absence de courant dans les bobines, une aiguille aimantée s'oriente comme l'indique la
figure 3
Lorsque les bobines sont parcourues par un courant I , le pôle Nord de l'aiguille tourne d'un angle
α dans le sens indiqué par la flèche.
Expliquer la rotation de l'aiguille, compléter la figure 3 et indiquer le sens du courant
En déduire la relation littérale entre B champ créé par le courant, BH et α.
3) – Les 2 bobines sont maintenant placées de sorte que leur plan soit perpendiculaire au plan du
méridien magnétique ( figure 4 )
En l'absence de courant dans les bobines, une aiguille aimantée s'oriente comme l'indique la
figure 4.
Lorsque les bobines sont parcourues par un courant I , l'aiguille tourne de 180°.
Expliquer la rotation de l'aiguille, compléter la figure 4 et indiquer le sens du courant.
-En déduire la valeur minimum de B et de I pour que l'aiguille tourne de 180°
18

Chapitre 1 Champs et Interactions Leçon 3 Champ magnétique
Figure 1 Figure 2
Figure 3 Figure 4
________________________________________________
1. a)
R
R
N
S
I
B
r
b) Le graphe B = f(I) est une droite passant par l’origine, donc B est proportionnel à I :
B = kI
Calcul du coefficient directeur k :
19

Chapitre 1 Champs et Interactions Leçon 3 Champ magnétique
soit un point A (5,0 A ; 4,0.10-3 T) k =
A
A
I
B k = 8,0.10-4 T.A-1 B = 8.10-4 I
B en teslas et I en ampères.
2. En l’absence de courant dans les bobines, l’aiguille s’oriente dans le plan du méridien
magnétique, suivant composante horizontale du champ magnétique terrestre, ayant le
sens SN de l’aiguille.
H
B
v
H
B
v
Le passage du courant dans les bobines crée un champ B
r
colinéaire à l’axe des bobines :
l’aiguille s’oriente alors suivant : T
B= B
r
+ H B
v
. Le sens de rotation donne le sens de B
r
. On
en déduit le sens du courant (d’après la règle de la main droite).
B
r et étant perpendiculaires, on en déduit d’après le schéma : tan
H
B
v
H
B
B
=α
3. En l’absence de courant, l’aiguille s’oriente, comme dans 2, suivant . Le champ
H
B
vB
r
créé
par le passage du courant dans les bobines étant colinéaire à l’axe des bobines, B et
r
H
B
v
sont
colinéaires. L’aiguille s’oriente suivant T
B= B
r
+ H B
v
.
α
H
B
r
B
r
Figure 3
complétée
- si B et sont de même sens, l’aiguille ne tourne pas.
r
H
B
v
- si B et sont de sens contraire, l’aiguille ne tourne de 180° que si B > B
r
H
B
v
H ⇒
B > 2,0.10-5 T . Du sens de B
r
, inverse du sens de H B
v
, on déduit le sens de I.
Valeur minimale de I : d’après la 1ère question, I =
k
B I = 4
5
10.8
10.2
−
−
I = 2,5.10-2 A
Pour que l’aiguille tourne de 180°, il faut I > 25 mA
R
H
B
r
B
r
S N
Figure 4
complétée
20