ch2 modélisation de l`atmosphère par beau temps

modélisation électrique de l'atmosphère par beau temps
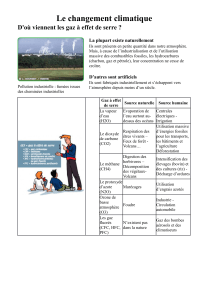
On représente l'atmosphère par beau temps par le milieu contenu entre les armatures d'un
condensateur, qui sont d'une part le sol, supposé parfaitement conducteur, et l'ionosphère, zone
conductrice située à l'altitude H, assimilée également à un plan parfaitement conducteur. On appelle S
la surface des armatures et Oz l'axe vertical ascendant.
z
ce milieu est de permittivité επ
0
9
10
36
=
−
F.m
-1
ionosphère H
sa conductivité est γ γ =
0
e
z
a
(
γ
0
et a constantes )
il est parcouru par un courant ascendant I
0
réparti I
0
uniformément sur la surface S sol O
données numériques : H = 50,0 km a = 4,00 km
S = 5,09 10
14
m
2
I
0
= -1500 A (signe !)
1. étude des champs de vecteurs et du potentiel
1.1 exprimer le vecteur densité de courant
r
j . Que peut-on en dire ?
1.2 exprimer le vecteur champ électrique
r
E
en fonction de l'altitude z.
1.3 au niveau du sol E(z=0) = -100 V.m
-1
. En déduire la valeur de
γ
0
.
1.4 calculer la différence de potentiel entre un point d'altitude z = 1,80 m et le sol. Pourquoi un
homme debout n'est-il pas électrocuté ?
2. étude des charges portées par les "armatures"
2.1 exprimer, puis calculer numériquement la charge surfacique
σ
0
portée par le sol, et la
charge totale Q
0
correspondante.
2.2 exprimer, puis calculer numériquement la charge surfacique
σ
H
portée par l'armature
supérieure, et la charge totale Q
H
correspondante.
3. étude de la charge contenue dans l'atmosphère
3.1 exprimer à partir du champ électrique la charge volumique ρ(z) de l'atmosphère. en
déduire sa valeur numérique au voisinage du sol.
3.2 calculer la charge totale Q
a
contenue dans l'atmosphère (armatures non comprises)
3.3 retrouver ce résultat d'une autre façon en se servant du résultat de la question 2..
4. calcul de la résistance de l'atmosphère
4.1 exprimer , puis calculer la différence de potentiel V
O
- V
H
.
4.2 la résistance de l'atmosphère est définie par R =( V
O
- V
H
) /I
O
; exprimer, puis calculer R.
4.3 est-il nécessaire que la valeur de H soit connue avec une grande précision? justifier.
____________________
(d'après INA-INSA)

modélisation électrique de l'atmosphère par beau temps
1. étude des champs de vecteurs et du potentiel
1.1on est ici en régime indépendant du temps, l'équation de conservation de la charge donne
0
z
j
jdiv
z
=
∂
∂
=
r
donc j
r
est à flux conservatif ; par ailleurs le courant s'obtient en calculant le flux de j
r
(qui ne dépend ni de x ni de y),à travers une surface orientée vers le haut :
kS.jI
0
r
r
= soit
k
S
I
j
0
rr =
; ce champ est uniforme.
1.2 le milieu suit la loi d'ohm donc Ej
r
r
γ= , en orientant la surface traversée par le courant vers le haut
on obtient: Eek
S
I
j
a/z
0
0
r
rr γ==
ce qui donne
ke
S
I
E
a/z
0
0
r
r
−
γ
=
1.3 au niveau du sol, E
0
= -100 V.m
-1
on en déduit avec k
S
I
)0(E
0
0
r
r
γ
= :
SE
I
0
0
0
=γ
A.N. γ
0
= 2,95 10
-14
Ω
-1
.m
-1
1.4 différence de potentiel entre un point d'altitude z = 1,80 m et le sol: on utilise la relation
∫
−=−
1
z
0
)1
d.E)0(Vz(V l
rr
qui donne :
∫
−
γ
−=−
1
z
0
a/z
0
0
)1
dze
S
I
)0(Vz(V =
a
z
S
I
a)1e(
S
I
a
1
0
0a/1z
0
0
γ
−≈−
γ
−
car z
1
<<a
A.N V(z
1
) -V(0) = 180 V
un homme debout ne serait pas électrocuté car sa conductivité étant bien plus élevée que celle de
l'atmosphère, il se comporte pratiquement comme un conducteur, donc surface équipotentielle au
potentiel du sol (0 V)
2. étude des charges portées par les "armatures"
2.1 charge surfacique
0
σ
portée par le sol :
au voisinage du sol, supposé être parfaitement conducteur, on trouve la charge surfacique en
appliquant le théorême de Gauss à un petit cylindre très plat contenant la charge
0
σ
ds (voir cours) ;
on retrouve ainsi le théorême de Coulomb : k)0(E
0
0
r
r
ε
σ
= et
0
σ
=ε
0
E
0
(<0) Q
0
=
0
σ
S=ε
0
E
0
S (<0)
A.N.
0
σ
= -8,84 10
-10
C.m
-2
Q
0
= -450 10
3
C
2.2 charge surfacique
H
σ
portée par l'armature supérieure :
de la même façon pour l'armature supérieure, mais cette fois, la normale à la surface est dirigée vers
le bas, d'où le signe "-" qui apparaît :
)k()H(E
0
H
r
r
−
ε
σ
= qui donne :
a/H
000H
eE)H(E
−
ε−=ε−=σ (>0) et Q
H
=
H
σ
S=-ε
0
E
0
e
-H/a
S ( >0)
A.N.
H
σ
= 3,29 10
-15
C.m
-2
Q
H
= 1,68 C
on remarque que Q
0
+ Q
H
≠ 0, ce n'est pas un condensateur, car il y a un milieu conducteur entre les
armatures;

3. étude de la charge contenue dans l'atmosphère
3.1 charge volumique ρ(z) de l'atmosphère, valeur numérique au voisinage du sol.
en utilisant la relation de Maxwell-Gauss :
0
Ediv ερ =
r
il vient :
a/z
0
00z
0
e
Sa
I
z
E
)z(
−
γ
ε
−=
∂
∂
ε=ρ
et au voisinage du sol :
)
a
z
1()
a
z
1(
Sa
I
)z(
0
0
00
−ρ=−
γ
ε
−=ρ
avec ρ
0
= 2,21 10
-13
C.m
-3
3.2charge totale Q
a
contenue dans l'atmosphère (armatures non comprises):
Q
a
=
∫∫∫∫
−
γ
ε
−=τρ
H
0
a/z
0
00
atm
Sdze
Sa
I
d)z( =
[
]
[
]
0
00a/H
0
00
H
0
a/z
0
00
I
1e
I
e)a(
a
Iγ ε
−≈−
γ
ε
=−
γ
ε
−
−−
car H>>a
A.N. Q
a
= 450 10
3
C
3.3 retrouvons ce résultat d'une autre façon : en prenant une surface de gauss entourant
complètement le milieu conducteur, et passant à l'intérieur des "armatures", (où le champ électrique
est nul), on obtient un flux total nul; donc la charge totale Q
a
+ Q
0
+Q
H
contenue dans cette surface
doit être nulle, soit
Q
a
= -Q
0
-Q
H
= -Sε
0
E
0
(-e
-H/a
+1) on retrouve bien la même expression car
S
I
E
0
0
0
γ
=
4. calcul de la résistance de l'atmosphère
4.1 la différence de potentiel V
O
- V
H
se calcule comme au 1.4:
∫
−
γ
−=−
0
H
a/z
0
0
dze
S
I
)H(V)0(V =
S
aI
)e1(
S
I
a
0
0a/H
0
0
γ
≈−
γ
−
car H>>a
4.2 résistance de l'atmosphère définie par R =( V
O
- V
H
) /I
O
:
S
a
)e1(
S
a
R
0
a/H
0
γ
≈−
γ
=
−
A.N. R = 266 Ω
4.3. Dans la mesure où H intervient dans le terme e
-H/a
<< 1 , il n'est pas nécessaire que sa valeur
soit connue avec une grande précision
__________________________