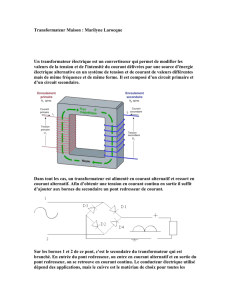
Transformateur parfait

Novembre
2006
TRANSFORMATEUR
MONOPHASE
TGE
L YCEE DU M T B LANC P HYSIQUE A PPLIQUEE 1/3
I- I NTRODUCTION
C’est un convertisseur d’énergie ; il transfère en alternatif la puissance électrique d’une source à une charge sans
changer la fréquence mais en adaptant les valeurs de U et I.
U
2
< U
1
→ abaisseur de tension
U
2
> U
1
→ élévateur de tension
U
2
= U
1
→ assure l’isolement entre la source et la charge.
II- P RESENTATION
SYMBOLE:
u
1
u
2
Convention récepteur convention générateur
III- L E TRANSFORMATEUR PARFAIT (T.P.)
3-1 Hypothèses
Pj = 0
Aucune perte ⇒ η = 1 P
fer
= P
h
+ P
F
= 0 ) circuit magnétique parfait
Pas de fuites magnétique ) (ni hystérésis, ni saturation)
(P
h
→ pertes par hystérésis et P
F
→ pertes par courant de Foucault)
3-2 relations fondamentales
En posant m =
1
2
N
N
appelé rapport de transformation , u
2
(t) = - m u
1
(t)
et U
2
= m. U
1
3-3 Formule de Boucherot
On retiendra U
1
= 4,44.N
1
.S.f.B
max
3-4 Relation entre les intensités
Dans l'hypothèse d'un circuit magnétique parfait , i
1v
= 0 et s
1
(t)=s
2
(t) ⇒ i
1
=u
2
.i
2
/u
1
Par conséquent, pour le T.P i
1
=
2
i
1
N
2N
−
i
1
(t) = - m i
2
(t) et I
1
= m.I
2
Application: U
1
= 230V U
2
= 48V et f = 50 Hz
Calculer I
2
et I
1
pour une charge R=10Ω et L=0,1H en série.
i
1
i
2
Carcasse métallique
ferromagnétique qui canalise
les lignes de champ.
N
1
spires pour l’enroulement primaire
N
2
spires pour l’enroulement secondaire

Novembre
2006
TRANSFORMATEUR
MONOPHASE
TGE
L YCEE DU M T B LANC P HYSIQUE A PPLIQUEE 2/3
IV- L E TRANSFORMATEUR REEL
4-1 Etude expérimentale
Schéma du montage: U
1
U
2
R
2
En faisant varier R
2
de sorte que I
2
varie de 0 à I
2N
, on relève
U
2
. On s'aperçoit que U
2
varie légèrement; U
2
dépend de I
2
.
On note ∆
∆∆
∆U = U
2V
- U
2
la chute de tension au secondaire.
Ceci nous amène à reconsidérer les hypothèses prises pour le transformateur parfait.
4-2 Les pertes dans le transformateur réel
- Pertes par effet Joule; Pj = r
1
.I
12
+ r
2
.I
22
(r
1
et r
2
représentent la résistance des enroulements.)
On peut donc modéliser ces pertes en associant au transformateur parfait une résistance au primaire (r
1
) et au
secondaire (r
2
)
- Pertes fer (pertes "magnétiques")
- Les lignes de champ ne sont pas totalement canalisées → existence de flux de fuite
- Les pertes par hystérésis et courant de Foucault entraînent un courant à vide non nul.
4-3 Bilan des puissances
Pabs = Pu + Pj + Pfer
On note parfois C les pertes cuivre (effet Joule) et F les pertes fer soit Pabs = Pu + C + F
Remarque: Les pertes fer dépendent de f et B
max
, donc à u
1
donné (U
1
et f sont constant), Pfer = cste
4-3-a Détermination des pertes nominales dans le fer
4-3-b Détermination des pertes nominales dans le cuivre:
Pour évaluer les pertes cuivre au fonctionnement nominal (r
1
I
1N2
+ r
2
I
2N2
),
4-3-c Rendement du transformateur réel
Par la méthode directe: η
ηη
η =
abs
u
P
P
=
abs
222
PcosIU
ϕ
ϕϕ
ϕ
Par la méthode des pertes séparées: η
ηη
η =
fercu222
222
PPcosIU cosIU +
++
++
++
+ϕ
ϕϕ
ϕ
ϕ
ϕϕ
ϕ

Novembre
2006
TRANSFORMATEUR
MONOPHASE
TGE
L YCEE DU M T B LANC P HYSIQUE A PPLIQUEE 3/3
V- M ODELE EQUIVALENT DU TRANSFORMATEUR REEL AU REGIME NOMINAL
5-1 Hypothèse de Kapp
En charge, on néglige le courant primaire à vide devant les courant primaire et secondaire en charge. Par
conséquent, le modèle du transformateur réel en charge (notamment au régime nominal) peut se "limiter" au
modèle équivalent vu du secondaire (de la charge):
jXs Rs
i
2
es = -m.u
1
u
2
Z
2
Zs
Il faut alors déterminer :
-Rs la résistance du transfo. ramené au secondaire
-Xs(=ls.ω) la réactance du transfo. ramené au secondaire.
5-2 Détermination expérimentale du modèle (Rs, Xs et m)
5-3-a Détermination du rapport de transformation
Grâce à l’essai à vide, on peut déterminer m =
1
v2
U
U
5-3-b Détermination de Rs et Xs
C’est l’essai en court-circuit qui permet de déterminer Rs et Xs. En effet,
P
1cc
= P
cu
= r
1
I
12
+ r
2
I
22
= Rs.(I
2cc
)
2
donc Rs =
2cc2
cc1
I
P
Par ailleurs, quelque soit la charge ; U
2
+ Zs.I
2
= Es = -mU
1
Ce qui s’écrit pour l’essai en court circuit, Zs.I
2cc
= - mU
1cc
soit Zs =
cc2
cc1
I
U
m
(ou encore Zs = m
2
U
1cc
/I
1cc
)
D’où on tire Xs =
22
RsZs −
−−
−
5-4 Détermination de la chute de tension au secondaire.
On utilise le schéma équivalent vu du secondaire :
E
s
= Zs.I
2
+ U
2
soit U
2v
= Zs .I
2
+ U
2
- Par Fresnel
222v2
UXsIRsIU +
++
++
++
+=
==
=
- Par le calcul approché :
∆
∆∆
∆U =
HB
AH
+
++
+
=
AB
⇒
⇒⇒
⇒ ∆
∆∆
∆U = R
s
I
2
cosϕ
ϕϕ
ϕ
2
+ X
s
I
2
sinϕ
ϕϕ
ϕ
2