Le redressement non commandé

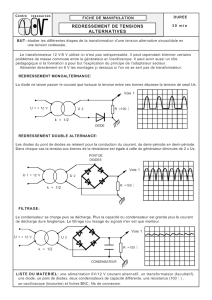
LE REDRESSEMENT NON COMMANDE
Presser la touche F5 pour faire apparaître les signets
qui favorisent la navigation dans le document.
Sommaire
1 Généralités ............................................................................................................................... 1
2 Montage parallèle..................................................................................................................... 1
2.1 Généralités − Règle de fonctionnement............................................................................ 1
2.2 Etude du montage P2 à cathode commune ....................................................................... 2
2.3 Etude du montage P2 à anode commune.......................................................................... 6
2.4 Etude du montage P3 à cathode commune ....................................................................... 7
2.5 Etude du montage P3 à anode commune........................................................................ 10
3 Montage parallèle double....................................................................................................... 11
3.1 Généralités − Règle de fonctionnement.......................................................................... 11
3.2 Etude du montage PD2 ................................................................................................... 11
3.3 Etude du montage PD3 ................................................................................................... 13
4 Montage série......................................................................................................................... 16
4.1 Généralités ...................................................................................................................... 16
4.2 Etude du montage S3 ...................................................................................................... 16
5 Groupement de montages redresseurs ................................................................................... 19
5.1 Groupement en série ....................................................................................................... 19
5.2 Groupement en parallèle................................................................................................. 20
6 Utilisation des redresseurs − Problèmes posés par les systèmes réels .................................. 22
6.1 Influence du facteur de forme du courant débité............................................................ 22
6.2 Dimensionnement de l'inductance de lissage ................................................................. 23
6.3 Choix du transformateur ................................................................................................. 23
6.4 Chutes de tension ............................................................................................................ 24
6.5 Caractéristique de sortie − Rendement ........................................................................... 26
6.6 Perturbations induites dans le réseau.............................................................................. 26
6.7 Comparaison des montages redresseurs − Critère de choix ........................................... 27
7 Etude du débit sur circuit capacitif ........................................................................................ 28
7.1 Généralités ...................................................................................................................... 28
7.2 Débit sur circuit RC ........................................................................................................ 28
7.3 Application à l'alimentation stabilisée avec régulateur de tension................................. 30
7.4 Remarque: Problèmes posés par la mise sous tension de ce type de montage............... 32

RE 1
LE REDRESSEMENT
A Redressement non commandé
1 Généralités
Les dispositifs redresseurs peuvent se classer en trois catégories: parallèle, parallèle double
et série. Dans un premier temps nous ferons donc une étude théorique de ces différents monta-
ges, en envisageant pour terminer les possibilités de groupement des redresseurs.
L'étude théorique se faisant en supposant que le courant débité est strictement constant et
que tous les éléments constitutifs sont parfaits, nous serons amenés, dans un deuxième temps,
à étudier les influences, d'une part de la nature de la charge, d'autre part des différents éléments
parasites. Dans cette partie, nous signalerons également les problèmes qui peuvent se poser vis
à vis du réseau d'alimentation et nous donnerons quelques indications sur le choix d'un monta-
ge redresseur.
Dans la dernière partie, nous ferons une étude succincte du filtrage par condensateur et de
son application à l'alimentation des régulateurs de tension. Ceci nous permettra en particulier
de montrer comment on peut traiter les cas des montages fonctionnant en courant interrompu.
Remarque: Pour que l'étude soit complète, nous supposerons toujours que le dispositif redres-
seur est alimenté par son propre transformateur, dont nous donnerons les caractéristiques en
fonction du type de montage et de ses grandeurs de sortie. Ces caractéristiques sont évidem-
ment inutiles si les paramètres du réseau électrique sont compatibles avec une alimentation
directe du montage redresseur.
2 Montage parallèle
2.1 Généralités − Règle de fonctionnement
Un montage parallèle est constitué par un groupe de redresseurs ayant tous une électrode
commune et alimenté par un système équilibré de tensions en étoile. Ces montages sont notés
Pq, où q désigne le nombre de phases du système de tensions.
L'électrode commune pouvant être constituée, soit par l'anode, soit par la cathode, on distin-
gue deux sous-catégories:

RE 2
− montage parallèle à cathode commune ( figure 1 )
En courant ininterrompu , leur règle de fonctionnement est la suivante:
− Les diodes conduisent à tour de rôle.
− La diode qui conduit est celle dont l'anode est au plus haut potentiel.
− montage parallèle à anode commune ( figure 2 )
En courant ininterrompu , leur règle de fonctionnement est la suivante:
− Les diodes conduisent à tour de rôle.
− La diode qui conduit est celle dont la cathode est au plus bas potentiel.
Il faut noter qu'une des sorties du montage est prise sur le point commun du système de ten-
sions. Au niveau des applications pratiques, les montages parallèles ne peuvent donc être ali-
mentés que par des réseaux où ce point est accessible ( par exemple, distribution triphasée
avec neutre sorti ).
2.2 Etude du montage P2 à cathode commune
2.2.1 Allure des tensions et des courants
Posons e1 = −e2 = E2sinθ avec θ = ω0t. Pour pouvoir compa-
rer les potentiels d'anode, il nous faut, dans un premier temps,
choisir une origine des potentiels. Pour les montages de type
parallèle, on prend le point commun des alimentations ( donc
le point milieu du secondaire ici ). Avec cette origine, le poten-
tiel d'anode de D1 est égal à e1 et celui de D2 est égal à e2. Le
tracé de ces tensions permet donc de déterminer immédiate-
ment les intervalles de conduction des diodes par application
de la règle de fonctionnement, puis d'en déduire les allures des
différentes grandeurs en raisonnant comme suit:
− Les diodes qui conduisent se comportent comme des courts-circuits. On a donc u = ei, où i
est l'indice de la diode qui conduit. De même, vD1 = 0 lorsque D1 conduit et vD1 = e1 − u
lorsque D1 est bloquée ( comme, dans ce cas, c'est D2 qui conduit, on a donc simplement
vD1 = e1 − e2 ).
D1
e1
D2
e2
Dq
eq
u
fi
gure 1
i
D2
i
s2
e2 u
up
e1
i
p vD
IC
i
D1
i
s1
D2
D1
fi
gure 3
D
'
1
e1
D
'
2
e2
D
'
q
eq
u
fi
gure 2

RE 3
− Les diodes conduisant à tour de rôle,
tout le courant IC transite par la diode
conductrice. Ainsi, par exemple, iD1 = IC
lorsque D1 conduit et iD1 = 0 sinon.
− Les courants au secondaire du transfor-
mateur sont respectivement égaux aux
courants dans les diodes ( il est donc inu-
tile de les tracer ici ). Par contre, du fait
de leur forme, il faut, pour obtenir ip, uti-
liser les équations aux intensités du trans-
formateur en régime non sinusoïdal ( Cf.
annexe ). De ces équations on déduit que,
comme les courants is1 et is2 ont même
valeur moyenne, le courant primaire est
donné par ip = n(is1 − is2), en notant, pour
simplifier l'écriture, n le rapport des
nombres de spires ( nous utiliserons cette
notation dans tout ce qui suit − n est bien
sûr défini ici pour un demi-enroulement,
ce qui entraîne par ailleurs que E = nU en
appelant U la valeur efficace de la tension
d'alimentation up ).
Annexe: Courant au primaire d'un transformateur parfait débitant un courant périodique non
sinusoïdal
1er cas: Le transformateur comporte un seul enroulement au secondaire
Le transformateur étant supposé parfait, il est en particulier linéaire et
on peut, pour déterminer ip, utiliser le théorème de superposition. Dans
cette optique, on décompose le courant secondaire is en sa valeur moyenne
IsC, a priori non nulle, et en sa composante alternative isalt, de même pé-
riode que is et de valeur moyenne nulle. Pour obtenir ip, on raisonne alors
comme suit:
− La force magnétomotrice N2IsC étant constante, elle ne crée pas de variation de flux et n'est
donc pas compensée par un appel de courant au primaire.
− La force magnétomotrice N2isalt, variable dans le temps, appelle un courant au primaire tel
qu'il y ait en permanence compensation des ampère-tours correspondants, c'est à dire tel que
N1ip = N2isalt. En remplaçant isalt par is − IsC, on obtient donc N1ip = N2(is − IsC), soit, finalement,
()
iN
NiI
pssC
=−
2
1
N2
N1
i
s
i
p
fi
gure 5
u
vD1
π 2π
π 2π
π 2π
π 2π
e
1 e2
D
1 D2 D1
θ
IC
i
s1 =
i
D1
θ
IC
i
s2 =
i
D2
θ
−nIC
nIC
i
p
θ
fi
gure 4

RE 4
2e cas: Le transformateur comporte plusieurs enroulements au secondaire
Toujours en utilisant le principe de superposition, il suffit d'appliquer le
raisonnement précédent à chacun des enroulements secondaires. A titre
d'exemple, si le secondaire est à point milieu, et si les sens des courants
sont ceux indiqués ci-contre, on aura
()()
iN
NiI N
NiI
pssC ssC
=−−−
2
1
11
2
1
22
,
soit
()
[]
iN
Nii I I
psssCsC
=−−−
2
1
12 1 2
Dans le cas, fréquent en électronique de puissance, où les courants secondaires ont même
valeur moyenne, la relation précédente se réduit à
()
iN
Nii
pss
=−
2
1
12
Remarque: Les relations précédentes s'appliquent sans restrictions aux transformateurs tripha-
sés dont le primaire est couplé en triangle ou en étoile avec neutre. Dans le cas d'un couplage
en étoile sans neutre, elles ne restent vraies que si la somme des forces magnétomotrices alter-
natives au secondaire est nulle. Si ce n'est pas le cas, le problème est plus complexe. Nous y
reviendrons ultérieurement en excluant pour le moment les rares montages où cette condition
n'est pas réalisée.
2.2.2 Calcul des grandeurs caractéristiques
2.2.2.1 Valeur moyenne de u
Les tracés étant faits en portant en abscisse la variable θ, nous raisonnerons dans tout ce qui
suit à partir de cette dernière. Ceci entraîne en particulier que la période des différentes gran-
deurs sera une grandeur angulaire exprimée en radians. Ici, la période de u est égale à π. En
prenant comme intervalle d'intégration [0;π], sur lequel u est égal à e1, on a
[]
UEd
E
C==−
∫
122
00
πθθ πθπ
π
sin cos
d'où, finalement, UE
C=22
π
2.2.2.2 Coefficient d'ondulation de u
De
kuu
UC
=−
max min
2, avec umax = E2, u
min = 0 et UE
C=22
π
, on tire kE
E
=2
222
π
, soit
k=≅
π
479%
N2
N2
N1
i
s2
i
s1
i
p
fi
gure 6