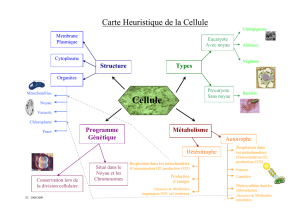
Quelques aspects des chaînes de Markov

Quelques aspects des chaînes de Markov
Djalil Chafaï
Décembre 2006, Biskra, Algérie.
Compilé le 18 janvier 2007

2
Fig. 1 – Andrei Andreyevich Markov
Copyright c 2006, B. Bercu & D. Chafaï. 2.0 du 2006-12-01. Document électronique créé le 18 janvier 2007, 22:39. Page n˚2.

Table des matières
0.1 Suites ou chaînes ? .................................. 5
0.2 La propriété de Markov forte ............................. 10
0.3 Les chaînes dans tous leurs états ........................... 11
0.4 Simulation d’une chaîne de Markov ......................... 14
0.5 Atteinte, absorption, harmonicité, martingales ................... 16
0.6 Invariance et récurrence positive ........................... 18
0.7 Loi forte des grands nombres ............................. 20
0.8 Périodicité ....................................... 23
0.9 Convergence en loi et couplage ............................ 24
0.10 Réversibilité et noyau de Metropolis-Hastings ................... 27
0.11 Estimation du noyau et de la mesure invariante .................. 31
0.12 Cas des espaces d’états finis ............................. 32
0.12.1 Récurrence, invariance, apériodicité, ergodicité ............... 32
0.12.2 Convergence géométrique vers l’équilibre et couplage ........... 35
0.12.3 Temps de recouvrement ........................... 36
0.13 Coalescences et algorithme de Letac-Propp-Wilson ................. 37
0.13.1 Coalescences de suites récurrentes aléatoires ................ 37
0.13.2 Algorithme de Letac-Propp-Wilson ..................... 39
0.14 Quelques exemples classiques ............................ 39
0.14.1 Processus de vie ou de mort sur N...................... 39
0.14.2 Marche aléatoire simple sur Zd........................ 41
0.14.3 Urne d’Ehrenfest ............................... 44
0.14.4 Modèle de Wright-Fisher ........................... 46
0.14.5 Google et Pagerank .............................. 52
Bibliographie 55
3

4TABLE DES MATIÈRES
Copyright c 2006, B. Bercu & D. Chafaï. 2.0 du 2006-12-01. Document électronique créé le 18 janvier 2007, 22:39. Page n˚4.

Quelques aspects des chaînes de
Markov
Ce chapitre est consacré aux chaînes de Markov homogènes à espace d’état au plus dénom-
brable. Leurs trajectoires peuvent se concevoir comme celles de suites récurrentes aléatoires
(Xn)de la forme Xn+1 =g(Xn, Un)où les (Un)sont indépendantes et équidistribuées. Tout
comme les martingales, les chaînes de Markov sont des suites de variables aléatoires caracté-
risées par une forme particulière de dépendance, qui leur confère des propriétés remarquables,
et un rôle important en modélisation. Les chaînes de Markov ont été introduites par Andrei
Andreyevich Markov vers 1906, à l’âge de cinquante ans, dans son article [23].
Dans toute la suite, un ensemble au plus dénombrable Eest toujours muni de la topologie (et
tribu) de toutes ses parties, qui rend continue (et mesurable) toute fonction f:E→R. Une me-
sure de Borel µsur Evérifie µ(A) = Px∈Aµ(x)pour tout A⊂E, où µ(x) := µ({x})∈R+. Une
fonction f:E→Rest µ-intégrable lorsque la somme au plus dénombrable Px∈E|f(x)|µ(x)
converge, et dans ce cas, REf(x)dµ(x) = Px∈Ef(x)µ(x). On dit qu’une mesure µsur Echarge
l’état x∈Elorsque µ(x)>0. Les mesures sont toujours supposées non identiquement nulles :
elles chargent donc au moins un état.
La seconde partie du chapitre est consacrée au cas particulier des chaînes de Markov à
espace d’état fini. Leur étude bénéficie de la théorie des matrices.
0.1 Suites ou chaînes ?
Soit (Xn)une suite de variables aléatoires à valeurs dans un ensemble au plus dénombrable
E. La loi de la suite (Xn)est une loi sur ENmuni de la tribu engendrée par les cylindres. En
vertu d’un célèbre théorème de Carathéodory, la loi de la suite (Xn)est caractérisée par ses
marges de dimension finie, c’est-à-dire par la loi des vecteurs aléatoires (X0, . . . , Xn)pour tout
n∈N. Or Eest au plus dénombrable, et donc la loi de (X0, . . . , Xn)est caractérisée à son tour
par la donnée de P(Xn=xn, . . . , X0=x0)pour tout x0, . . . , xndans E. À ce stade, on peut
écrire par conditionnements successifs
P(Xn=xn, . . . , X0=x0) =
n−1
Y
k=0
P(Xk+1 =xk+1 |Xk=xk...,X0=x0)P(X0=x0).
5