Chp. 8. Méthodes Newtoniennes

Chp. 8. M´ethodes Newtoniennes
Avertissement! Dans tout ce chapˆıtre, Ωd´esigne un ouvert de IR n, et fune fonction de classe
C2sur Ω.
8.1 L’algorithme de Newton
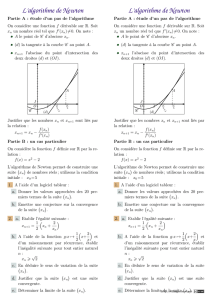
L’algorithme de Newton combine la strat´egie de Newton de choix de la direction de descente
avec, `a chaque ´etape, une recherche du pas optimal :
Newton(f,x0, tolerance)
x←x0,g← ∇f(x0),H← ∇2f(x0)
Tant que : gTH−1g≥tolerance
Calculer le pas optimal tdans la direction : u=−H−1g
x←x+t u,g← ∇f(x),H← ∇2f(x)
Retourner x
Le calcul du pas optimal s’effectue en pratique au moyen d’une proc´edure unidimensionnelle comme
GoldenSearch, ou QuadSearch. Le calcul de ∇2f(x)−1`a chaque it´eration requiert une proc´edure
d’inversion de matrice rapide et robuste :factorisation de Cholesky si la Hessienne reste toujours
d´efinie positive, LU , ou : QR.
Le choix du test d’arrˆet, qui mesure la norme du gradient pour la m´etrique associ´ee `a l’inverse
de la Hessienne, se justifie par l’invariance de l’algorithme par changement d’´echelle qui en r´esulte
(paragraphe 8.2).
8.2 Invariance par changement d’´echelle
Posons : f(x) = g(D x), o`u : Dest une matrice diagonale de termes diagonaux non nuls. Pour
minimiser f`a partir de l’initialisation x0, on peut utiliser indiff´eremment : Newton(f,x0, tolerance)
ou : Newton(g,y0, tolerance), avec : y0=D x0. Le passage d’un algorithme `a l’autre correspond
simplement `a un changement d’´echelle .
Exemple 8.1 n= 2,f(x, y) = x2+ 100 y2,D=Ã1 0
0 10 !, et : g(x, y) = x2+y2

Universit´e Paris Dauphine iup.gmi
Tous les algorithmes de gradient sont sensibles aux changements d’´echelle (cf. exemples 6.2 et
6.3 page 29) qui modifient le conditionnement de la Hessienne, et donc le taux de convergence de
l’algorithme. Cette sensibilit´e induit en pratique un probl`eme souvent d´elicat de choix des ´echelles.
L’algorithme de Newton est au contraire invariant par changement d’´echelle.
Th´eor`eme 8.1 Si Dest une matrice diagonale, de termes diagonaux non nuls, les algorithmes :
Newton(f,x0, tolerance) et : Newton(g,y0, tolerance), o`u : y0=D x0, et : f(x) = g(D x)
sont de mˆeme nature : tous deux divergents ou tous deux convergents. Lorsqu’ils convergent, leurs
tests d’arrˆet respectifs sont v´erifi´es apr`es un mˆeme nombre d’it´erations et les suites xket ykcon-
struites par les deux algorithmes se d´eduisent l’une de l’autre par changement d’´echelle : yk=D xk.
Preuve : Si : y=D x, on a : ∇f(x) = D∇g(y), et : ∇2f(x) = D∇2g(y)D. Supposons qu’apr`es
kit´erations : yk=D xk, d’o`u :
∇f(xk)T∇2f(xk)−1∇f(xk) = ∇g(yk)TD D−1∇2g(yk)−1D−1D∇g(yk)
=∇g(yk)T∇2g(yk)−1∇g(yk)
Ou bien la valeur commune : ∇f(xk)T∇2f(xk)−1∇f(xk) = ∇g(yk)T∇2g(yk)−1∇g(yk) est inf´erieure
`a tolerance, et les deux algorithmes s’arrˆetent apr`es la k`eme it´eration, ou bien les directions de
Newton : uk=−∇2f(xk)−1∇f(xk) , et : vk=−∇2g(yk)−1∇g(yk) v´erifient :
D uk=−D∇2f(xk)−1∇f(xk) = −D D−1∇2g(yk)D−1D∇g(yk)
=− ∇2g(yk)−1∇g(yk) = vk
En posant : ϕ(t) = f(xk+t uk) et : ψ(t) = g(yk+t vk), on a dans le second cas :
ϕ0(t) = ∇f(xk+t uk)Tuk=∇g[D(xk+t uk)]TD uk=∇g(yk+t vk)Tvk=ψ0(t)
donc le mˆeme pas tkest optimal au point xkdans la direction uket au point ykdans la direction
vk, et : yk+1 =yk+tkvk=D xk+t D uk=D(xk+tkuk) = D xk+1.
2
8.3 Convergence de l’algorithme de Newton
Th´eor`eme 8.2 Si Ωest un bassin d’ellipticit´e de f, l’algorithme de Newton converge, pour toute
initialisation x0dans Ωvers l’unique minimum x?de fdans Ω.
Preuve : La d´emonstration reprend le plan de la d´emonstration du th´eor`eme de convergence de
l’algorithme du gradient `a pas optimal. Pour tout point xkconstruit par l’algorithme, on pose,
pour simplifier les notations :
gk=∇f(xk), Hk=∇2f(xk),et : uk=−H−1
kgk
Par construction, la suite fkest strictement d´ecroissante. La suite des points construits par l’algo-
rithme reste ainsi contenue, `a partir de tout rang : k≥0, dans l’ensemble convexe compact Skde
niveau fkde fdans Ω, et il existe donc, pour tout indice k≥0, des constantes cet Ktelles que :
∀x∈Skc Id ≤ ∇2f(x)≤K Id(1)
gmi1.opti. G.L. cours – 02/05 p. 45

Universit´e Paris Dauphine iup.gmi
On d´eduit alors du th´eor`eme 6.3 page 32 :
kxk−x?k ≤ c−1kgkk(2)
Puisque la suite des ensembles Skest d´ecroissante, toute constante d’ellipticit´e de fsur S0
est a fortiori une constante d’ellipticit´e de fsur Sk. La constante capparaissant dans (2) peut
donc ˆetre fix´ee ´egale `a une constante d’ellipticit´e de fsur S0, et, pour ´etablir la convergence de
l’algorithme, il suffit ainsi de prouver que la suite : gk=−Hkukconverge vers 0 dans IR n, donc
(lemme 6.1, page 30) que la suite ukconverge vers 0 dans IR n. En remarquant que la suite r´eelle
fkest strictement d´ecroissante et born´ee inf´erieurement par f(x? ), ce r´esultat est cons´equence de :
fk+1 ≤fk− − c2
2Kkukk2
(3)
Pour ´etablir (3), posons : ϕ(t) = f(xk+t uk). Puisque : ϕ0(0) = gT
kuk=−uT
kHkuk<0, on a
n´ecessairement : f(xk+t uk) = ϕ(t)< ϕ(0) = fkpour : t > 0 suffisamment petit, donc : xk+t uk∈Sk.
Tant que xk+t ukreste dans Sk, on d´eduit de la formule de taylor-Lagrange, appliqu´ee `a ϕ
sur l’intervalle [ 0, t ] : ϕ(t) = ϕ(0) + t ϕ0(0) + t2
2ϕ00(θ), o`u : θ∈] 0, t [ , soit :
f(xk+t uk) = fk+t gT
kuk+t2
2uT
k∇2f(xk+θ uk)uk
et, en utilisant (1) :
f(xk+t uk)≤fk−t uT
kHkuk+Kt2
2kukk2≤fk−tkukk2µc−Kt 2¶
(4)
qui prouve que l’intervalle : [ xk, xk+2c
Kuk] reste tout entier contenu dans Sk. Pour t=c Ken
particulier, on obtient finalement dans (4) : fk+1 ≤f(xk+c
Kuk)≤fk−c2 2Kkukk2.
2
8.4 Comportement asymptotique du pas
Th´eor`eme 8.3 Si l’algorithme de Newton converge vers un minimum local non d´eg´en´er´e x?de f,
et l’application : x7→ ∇2f(x)est Lipschitzienne sur un voisinage de x?, le pas optimal tend vers
un.
Preuve : On reprend les notations utilis´ees dans la d´emonstration du th´eor`eme 8.2 :
gk=∇f(xk), Hk=∇2f(xk),et : uk=−H−1
kgk
et on note tkle pas optimal dans la direction uk, de sorte que : xk+1 =xk+tkuk.
Puisque x?est un minimum local non d´eg´en´er´e de f, on peut trouver : α > f (x?
) suffisamment
voisin de f(x? ), et : r > 0 suffisamment petit pour que l’ouvert :
Ω = {x∈IR n| k x−x?k< r et f(x)< α }
soit un bassin d’ellipticit´e (cf. 5.5 page 25) de f, et que x7→ ∇2f(x) soit Lipschitzienne sur Ω.
Pour k≥0 suffisamment grand, l’intervalle [ xk, xk+1 ] reste contenu dans Ω. La fonction ϕ
d´efinie par : ϕ(t) = f(xk+t uk) est donc C2sur l’intervalle [ 0, tk], et :
0≤t≤tk⇒ | ϕ00(t)−ϕ00(0) |=¯¯¯uT
k[∇2f(xk+t uk)− ∇2f(xk)] uk¯¯¯≤t L kukk3
(5)
gmi1.opti. G.L. cours – 02/05 p. 46

Universit´e Paris Dauphine iup.gmi
o`u : Lest une constante de Lipschitz de x7→ ∇2f(x) sur Ω.
Par ailleurs, en appliquant `a ϕ0la formule de Taylor-Lagrange sur [ 0, tk], on peut ´ecrire :
0 = ϕ0(tk) = ϕ0(0) + tkϕ00(θ), θ ∈] 0, tk[(6)
En combinant (6) et (5), il vient :
¯¯¯(tk−1) uT
kHkuk¯¯¯=|ϕ0(0) + tkϕ00(0) |=tk|ϕ00(0) −ϕ00(θ)|
≤θ tkLkukk3≤t2
kLkukk3
d’o`u, en utilisant l’assertion (1) de la d´emonstration du th´eor`eme 8.2 :
c|tk−1| ≤ t2
kLkukk=tkLkxk+1 −xkk(7)
o`u : cest une constante d’ellipticit´e de fsur l’ensemble de niveau fkde fdans Ω, ce qui suffit `a
´etablir la convergence de tkvers un.
2
8.5 Vitesse de convergence
Th´eor`eme 8.4 Sous les hypoth`eses du th´eor`eme 8.3, la vitesse de convergence de l’algorithme de
Newton est quadratique.
Preuve : On reprend les notations utilis´ees dans la d´emonstration du th´eor`eme 8.3 :
•gk=∇f(xk), Hk=∇2f(xk), uk=−H−1
kgk,et : xk+1 =xk+tkuk
•Ω est un bassin d’ellipticit´e de fcontenant x?
.
• ∀x∈Ωc Id ≤ ∇2f(x)≤K Id
•x7→ ∇2f(x) est Lipschitzienne de constante Lsur Ω.
Pour tout k≥0 suffisamment grand, l’intervalle [ xk, x?] reste contenu dans Ω. Il s’agit alors
d’´etablir, en supposant la suite xkconstruite par l’algorithme infinie :
lim
k7→+∞
kxk+1 −x?k
kxk−x?k2<+∞
Puisque le pas optimal tktend vers un, c’est une cons´equence de l’in´egalit´e triangulaire :
kxk+1 −x?k=kxk+tkuk−x?k ≤ k xk+uk−x?k+|1−tk| k ukk
qui, combin´ee `a l’assertion (7) de la d´emonstration du th´eor`eme 8.3 donne :
kxk+1 −x?k ≤ k xk+uk−x?k+t2
kc−1Lkukk2
et des in´egalit´es :
kxk+uk−x?k ≤ c−1Lkxk−x?k2
(8)
kukk ≤ c−1Kkxk−x?k(9)
•Pour ´etablir (8), on d´efinit une fonction gde classe C
|[2] sur Ω en posant :
g(x) = f(x)−1
2(x−x?
)THk(x−x?
)
gmi1.opti. G.L. cours – 02/05 p. 47

Universit´e Paris Dauphine iup.gmi
de sorte que, pour tout vecteur ude IR net tout point xde l’intervalle [ xk, x? ] :
¯¯¯uT∇2g(x)u¯¯¯=¯¯¯uT∇2f(x)u−uTHku¯¯¯=¯¯¯uT[∇2f(x)− ∇2f(xk)] u¯¯¯
≤Lkuk2kx−xkk ≤ Lkuk2kxk−x?k
et l’on d´eduit alors du lemme 6.2 page 30 appliqu´e `a gsur l’intervalle [ xk, x?
], en remarquant que
∇g(x?
) = 0 :
k ∇g(xk)− ∇g(x? )k=kgk+Hk(xk−x? )k ≤ Lkxk−x?k2
Finalement, puisque : uk=−H−1
kgk, il r´esulte de (1) :
ckxk−x?
−ukk2≤(xk−x?
−uk)THk(xk−x?
−uk)
= (xk−x? −uk)T[gk+Hk(xk−x? )]
≤ k xk−x? −ukkLkxk−x?k2
d’o`u le r´esultat.
•Pour ´etablir (9), on applique cette fois directement le lemme 6.2 `a la fonction fsur l’intervalle
[xk, x?
], en remarquant que ∇f(x?
) = 0 :
kgkk=k ∇f(xk)− ∇f(x?
)k ≤ Kkxk−x?k
d’o`u, en utilisant Cauchy-Schwarz et (1) :
ckukk2≤uT
kHkuk=−gT
kuk≤Kkukk k xk−x?k
2
8.6 Comparaison des algorithmes GradOpt, Fletcher-Reeves, et
Newton
On reprend le crit`ere : f=x4+ 4 y4+ 4 x y utilis´e pr´ec´edemment pour tester l’algorithme
de Fletcher-Reeves. La proc´edure utilis´ee pour la recherche lin´eaire est toujours la proc´edure
GoldenSearch. La valeur du param`etre tol´erance pass´e `a cette proc´edure est fix´ee `a : 10−8. Pour
l’algorithme de Newton, la Hessienne est invers´ee, sous MathematicaT M , en appelant la proc´edure
pr´ed´efinie d’inversion de matrice : Inverse[ ].
En compl`etant le tableau 7.2 page 42, on constate que l’algorithme de Newton est moins robuste
mais plus rapide que les divers algorithmes de gradient pr´ec´edemment utilis´es. Dans la derni`ere
colonne du tableau, la mention (( divergence )) indique en r´ealit´e que l’algorithme (( boucle )) : il
calcule en fait un point en lequel la direction de Newton n’est pas une direction de descente. La
proc´edure de recherche lin´eaire retourne alors ind´efiniment le mˆeme point.
Bien que particuli`erement simple, le crit`ere choisi pour ce test atteint son minimum sur IR 2
en deux points, obligeant l’algorithme de Newton `a choisir entre deux minima. Contrairement `a
la direction de Cauchy, la direction de Newton en un point non critique n’est pas n´ecessairement
une direction de descente, et plusieurs choix de l’initialisation mettent ainsi en ´echec la strat´egie
de Newton. On peut n´eanmoins esp´erer en pratique un comportement plus robuste lorsque le
gmi1.opti. G.L. cours – 02/05 p. 48