LES ANGLES

6ème 2005-2006
LES ANGLES
LES ANGLES
I.
I. L'essentiel L'essentiel
Définition
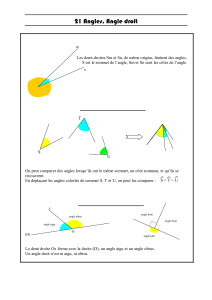
Un angle est une figure formée par deux demi-droites de même origine.
Codage
Un angle se code à l’aide d’un arc de cercle.
Vocabulaire
Les deux demi-droites s’appellent les côtés de l’angle.
L’origine commune s’appelle le sommet de l’angle.
Notations d’un angle
On note un angle à l’aide de trois lettres surmontées d'un chapeau. La lettre centrale indique
toujours le sommet.
Exemple
On considère un triangle MNP.
Fiche d'exercices " Vocabulaire et Notations "
- L'angle dont le sommet est N, les côtés [NM) et [NP) se note
PNM
ou
MNP
.
- L'angle dont le sommet est M, les côtés [MN) et [MP) se note
NMP
ou
PMN
.
- L'angle dont le sommet est P, les côtés [PN) et [PM) se note
NPM
ou
MPN
.
A
O
B
O est le sommet
[OA) et [OB) sont les côtés
M
P
N
Y
R
K
Cet angle se note
RKY
ou
YKR

II.
II. Mesurer un angle Mesurer un angle
1 ère é tape
Mesurer un angle, c'est mesurer l'ouverture formée par les deux côtés de l'angle.
A vue d’œil, la mesure de l’angle
OML
est plus grande que celle de
XGS
.
2 ème é tape
L'unité de mesure utilisée couramment pour les angles est le degré.Un degré se note « 1° ».
3 ème é tape
Le rapporteur est l’instrument qui permet de mesurer les angles.Chaque graduation représente
1°. On peut mesurer de 0° jusqu’à 180°.
O
L
M
G
S
X
L'angle de gauche mesure 8° car il contient huit
angles de 1°.
L'angle de droite mesure 1°. Il permet de mesurer
tous les angles.

4 ème é tape
Construire un angle droit à l’aide de l’équerre.
(Engager une discussion avec les élèves sur l'utilisation du rapporteur puis dégager une méthode générale à
l'oral)
5 ème é tape
Appliquer tout de suite la méthode trouvée pour mesurer ces deux angles.
Méthode générale
•Placer le centre du rapporteur (le trou ou la croix) sur le sommet de l’angle.
•Faire tourner le compas pour que la graduation 0 soit sur l'un des côtés.
•A partir de cette graduation 0, aller jusqu'au deuxième côté pour obtenir la mesure de
l'angle.
Codage
La mesure d'un angle peut s'indiquer sur la figure. Dans ce cas, on la note à coté de l'arc de
cercle qui code l'angle.
Fiche d'exercices « Mesurer un angle »
G
S
X
110°

III.
III. Angles particuliers Angles particuliers
1/ Angle droit
Définition
Un angle droit est un angle dont la mesure est égale à 90°.
Codage
Un angle droit se code à l’aide d’un petit carré (ou rectangle).
2/ Angle plat
Définition
Un angle plat est un angle dont la mesure est égale à 180°.
Remarque
Un angle plat contenient deux angles droits.
3/ Angle nul
Définition
Un angle nul est angle dont la mesure est égale à 0°.
4/ Angles aigus
Définition
Un angle aigu est un angle dont la mesure est comprise entre 0° et 90°.
Remarque
Un angle aigu peut toujours être contenu dans un angle droit. On peut ainsi vérifier la
cohérence d’une mesure par rapport à l’angle donné.
A Y
Z
On obtient un angle nul lorsque les deux côtés d'un angle sont confondus

5/ Angles obtus
Définition
Un angle obtus est un angle dont la mesure est comprise entre 90° et
180°.
Remarque
Un angle obtus peut toujours contenir un angle droit. On peut ainsi vérifier...
6/ Nature d'un angle
Préciser la nature d'un angle signifie qu'il faut indiquer s'il est aigu, obtus, droit ou plat.
Exemples
Le triangle EFG est contient trois angles aigus (triangle acutangle). Le triangle ABC contient
un angle obtus et deux angles aigus (triangle obtusangle). Un triangle rectangle contient...
Fiche d'exercices « Angles particuliers »
IV.
IV. Construire un angle de mesure donné Construire un angle de mesure donné
1/ Activité
Travailler avec les élèves pour arriver à construire un angle qui mesure 50° (par exemple). On pourra en
envoyer au tableau et ainsi engager des discussions.
2/ Méthode générale
•Trace une demi-droite.
•Place le centre du rapporteur sur l'origine de la demi-droite et le zéro de la graduation sur
au niveau de la demi-droite.
•Trace un trait correspondant à la graduation voulue puis le deuxième côté de l'angle.
3/ Application
Reproduire l'angle
ABC
à partir de la demi droite [Ox) puis à partir du point P.
EF
G
A
C
B