Département de physique

1
Département de physique
Principe d’un capteur de courant à zéro de flux
• Réalisations électroniques : Luc Floriot (assistant ingénieur)
• Travail expérimental et rédaction du document : Jean-Baptiste Desmoulins (P.R.A.G.)
mail : [e-mail]
Le système que nous cherchons à construire doit permettre de visualiser une tension, image du courant à
étudier, sur une plage de fréquence allant du continu jusqu’à la coupure haute. On peut alors envisager
différentes mesures sur la tension récupérée (valeur moyenne, valeur efficace, analyse du spectre, temps de
montée, etc…). Le système que nous allons décrire est utilisé, en pratique, pour observer des courants de fortes
valeurs (qq 10A). L’idée générale consiste à transformer le courant important étudié en un courant beaucoup plus
faible, proportionnel au précédent dans un rapport connu, indépendant, autant que possible, des conditions
expérimentales. Ce courant sera ensuite envoyé dans une résistance aux bornes de laquelle on récupèrera la
tension. Ce système permet d’éviter d’ajouter une impédance potentiellement perturbatrice dans le circuit étudié,
comme c’est le cas pour un ampèremètre
I. Mise en évidence de l’intérêt du fonctionnement à zéro de flux.
Pour comprendre l’intérêt de la structure à zéro de flux, nous allons commencer par décrire une structure plus
simple à priori mais dont nous mettrons en évidence les limites, qui sont intolérables pour un système de mesure.
Nous décrirons alors le principe de la structure à zéro de flux, puis nous verrons les problèmes posés par cette
structure et les précautions à prendre lors de sa mise en œuvre.
I .1. Structure la plus simple pour un capteur de courant .
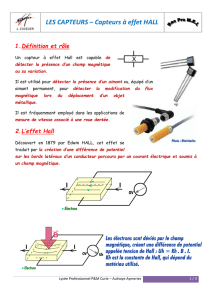
a/ capteur à effet Hall : principe et emploi dans le système étudié.
Le capteur à effet Hall permet de récupérer une image du flux magnétique qui traverse un barreau semi-
conducteur. Nous allons voir qu’on peut l’utiliser pour réaliser un capteur de courant (système qui délivre une
tension proportionnelle au courant à observer).

2
• Structure de base du capteur.
En simplifiant, on peut réaliser un capteur à effet Hall de la façon suivante :
On distingue un barreau de semi conducteur sur lequel arrivent quatre électrodes métalliques. On fait passer
un courant I entre les deux électrodes longitudinales. Nous allons chercher à comprendre ce qui se passe lorsque
l’ensemble est plongé dans le champ d’induction magnétique B orienté comme sur la figure.
Le capteur que nous avons utilisé est un composant discret (KSY10) intégré dans un boîtier pour permettre
une connexion plus facile de l’alimentation et de la tension de sortie. L’ensemble est présenté sur la
photographie suivante :
rq : la zone utile de semi conducteur est d’épaisseur e, de hauteur h et de longueur L. On peut par ailleurs
définir la section S du canal conducteur par S = e.h.
• Principe de fonctionnement.
Nous allons commencer par faire une représentation du système dans le plan Oxz
Nous allons supposer que la conduction (courant I) est assurée par les électrons (densité de porteur n et
mobilité µ). Sous l’action du champ magnétique, ces charges négatives vont être déviées vers l’électrode
transversale (2) (force de Lorentz). Cette accumulation de charges va provoquer l’apparition d’un champ
électrique E entre les électrodes transversales. Il va être à l’origine d’une force qui s’oppose à la force de
Lorentz. On finit par atteindre un régime stationnaire lorsque les deux forces s ‘équilibrent. Le champ électrique
qui règne alors entre les électrodes transversales explique la différence de potentiel VH qui existe entre elles. La
tension VH est appelée tension de Hall.

3
Quantitativement, on peut écrire qu’en régime stationnaire, on a
B.v.q
h
V
.qE.q H
H−=−=−
De plus S.v.n.qS.v.S.jI −=ρ==
r
v
r
r
où j est la densité de courant, ρ la densité volumique de charges, n le nombre de charges par unité de
volume, S la section de conducteur, v la vitesse moyenne des porteurs, I le courant considéré.
De ces deux équations, on déduit que
e
B.I
.K
e
B.I
.
n.q 1
VHH =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
=
• Ainsi, si on injecte un courant I connu fixé, on récupère une tension VH proportionnelle à B, que B soit
continu ou variable ce qui est un grand avantage par rapport aux capteurs de flux inductifs.
• Si on applique un champ magnétique B connu fixé, VH est directement proportionnel à I.
• Dans tous les cas, on remarque que KH est d’autant plus forte que la densité de porteurs est faible. Si on
veut une tension suffisante, il ne faudra pas doper trop fortement le matériau semi-conducteur.
• La densité de porteurs susceptibles de participer à la conduction va dépendre de la température. T va donc
avoir une influence sur KH.
b/ utilisation d’un capteur à effet Hall pour réaliser un capteur de courant.
Nous allons essayer de comprendre comment utiliser un capteur à effet Hall pour récupérer une tension
image d’un courant à étudier. Dans un premier temps, on peut envisager la structure simple suivante :
Le bobinage entourant le circuit magnétique est parcouru par un courant i(t). De ce courant va résulter un
champ d’induction Be proportionnel à i dans l’entrefer. En effet :
- le théorème d’ampère donne )t(i.Nl).t(HL).t(H ef
=
+
- Si on considère que le circuit magnétique canalise suffisamment les lignes de champ, on peut négliger
les flux de fuite et par conservation du flux, on aura
Be.Se = Bf.Sf
où Be et Bf représentent respectivement le champ d’induction moyen dans l’entrefer et dans le matériau
magnétique et où Se et Sf représentent respectivement la section de l’entrefer et du circuit magnétique.
- Si on suppose que le matériau magnétique est assez doux (faible champ coercitif) et qu’il n’est pas trop
saturé (hypothèse probable en raison de l’existence de l’entrefer), alors on peut raisonnablement définir
une perméabilité relative µr telle que
frof H.µ.µB
=
L’équation déduite du théorème d’ampère peut alors être transformée de la façon suivante :
i.Nl.
µ
B
L.
µ.µ
B
o
e
ro
f=+ ou encore i.N
µl
L.
µ.µ
SS
.B oro
fe
e=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
et ainsi )t(i.)t(Be
α
=
Si on place un capteur à effet Hall dans l’entrefer, il est soumis à Be. On peut alors imposer le courant I
continu, fixé le plus précisément possible, qui traverse le barreau de semi conducteur. On va alors récupérer une
tension VH proportionnelle à Be c’est à dire
)t(i.
e
..I
.K
e
B.I
.KV H
e
HH α
==
On peut alors faire un étalonnage et déterminer le coefficient de proportionnalité entre VH(t) et i(t).

4
I.2. Limites d’un tel capteur.
Ce type de capteur de courant présente un défaut important. En effet la courbe d’étalonnage peut être
modifiée par les conditions expérimentales (température, position du capteur, saturation magnétique…), ce qui la
rend caduque.
Sur la figure suivante, on présente la relation entre courant et tension image lorsqu’on augmente de courant
continu à observer puis qu’on le fait diminuer. Dans un cas, le capteur à effet Hall placé au centre de l’entrefer et
dans l’autre, il est légèrement excentré (1mm de décalage environ).
80
60
40
20
0
tension du capteur à effet Hall (mV)
2.01.51.00.50.0
courant (A)
capteur excentrée
capteur centré
entrefer de 5 mm
On constate qu’on ne part pas du point (0,0). Deux raisons peuvent expliquer ce problème. On ne part pas
d’un état parfaitement désaimanté, et le capteur à effet Hall présente une offset (mesuré à - 5 mV environ lors de
ces essais).
Lorsqu’on augmente le courant, les courbes présentent un effet d’hystérésis, caractéristique de l’ensemble du
circuit magnétique (matériau ferromagnétique et entrefer). Le fait de déplacer le capteur à effet Hall dans
l’entrefer change également notablement la réponse du système. On aurait également pu chauffer le capteur à
effet Hall et observer une modification de la réponse, mais cette expérience est plus délicate à réaliser
correctement, car il est difficile de maintenir la température constante avec les moyens dont nous disposons.
Les caractéristiques d’un tel dispositif ne sont donc pas facilement reproductibles, ce qui rend la structure
impropre à la réalisation d’un capteur de bonne qualité.
I.3. Principe du système à zéro de flux.
On peut alors envisager un système un peu plus complexe, mais moins sensible aux différentes perturbations
expérimentales. Pour cela, on va considérer la structure suivante :
Si on applique le théorème d’ampère à la structure suivante où Φ est le flux global dans le circuit, différence
entre Φ1 et Φ2 et ℜ est la réluctance de ce dernier, alors )t(.)t(i.N)t(i.N 2211
Φ
ℜ
=
+
Si on parvient à faire en sorte que Φ(t) soit nul, alors
)t(i.
N
N
)t(i 1
2
1
2−=
C’est grâce au capteur à effet Hall que l’on va réussir à détecter l’annulation du flux. L’intérêt de ce montage,
c’est que lorsque l’on cherche à mesurer un courant i1 de forte valeur, il suffit de prendre un rapport de spires
adapté afin de pouvoir se contenter de travailler avec i2 de beaucoup plus faible valeur mais directement
proportionnel à i1. On place alors une résistance de précision connue dans le circuit parcouru par i2 et on mesure
la tension à ses bornes.

5
Le lien entre le courant à observer et la tension de mesure ne dépend plus que de la valeur de la résistance de
mesure et du rapport du nombre de spires. La position et le gain du capteur n’ont plus d’incidence notable sur la
réponse de l’ensemble, puisque le rapport entre le flux dans le circuit et la tension de Hall n’intervient plus dans
la réponse en régime permanent. Par ailleurs, le circuit magnétique fonctionnant à flux nul en régime permanant
et à flux très faible lors des régimes transitoires, il n’y aura plus de problème d’hystérésis.
I.4. Réalisation pratique du capteur de courant à zéro de flux.
• Structure du système.
Pour parvenir à annuler le flux, on va construire le système de la façon suivante :
Dans le capteur à effet Hall, on fait à nouveau passer un courant continu I fixé le plus stable possible afin que
la tension de Hall VH détectée soit directement proportionnelle à la valeur du champ d’induction Be dans
l’entrefer. La tension VH est amplifiée et on peut placer un correcteur intégral ou proportionnel intégral pour
éliminer l’erreur statique sur VH ce qui conduit à un zéro de flux dans le circuit magnétique.
On a réalisé les circuits primaire et secondaire avec des bobines présentant respectivement 125 et 1000
spires. La résistance de mesure est une résistance de 15Ω environ supportant 200 mA. L’amplificateur de
puissance est un amplificateur Phytex ENSC 300. Le correcteur est réalisé à partir du boîtier ENSC325 (l’entrée
« + » du comparateur est l’entrée du correcteur et l’entrée « – » est mise à 0). Le capteur à effet Hall est celui qui
a été décrit précédemment.
• Mise en équation.
On peut alors écrire les équations suivantes
- La tension de Hall VH est proportionnelle à Be champ d’induction dans l’entrefer, lui même
proportionnel à la différence des flux Φ1 et Φ2. On a donc ).()p(V 21H
Φ
−
Φ
α
=
- Si G(p) représente le gain de l’ensemble amplificateur de tension/correcteur, et si on suppose que
l’amplificateur de puissance n’agit pas sur la tension mais seulement sur le courant, si L2 est l’inductance du
bobinage secondaire de N2 spires dont on néglige la résistance, on a )p(i).p.LR()p(V).p(G 22mH
+
=
- Sachant que i2 est beaucoup plus petit que i1, la relation entre i2 et Φ2 peut être supposée linéaire (pas de
saturation magnétique), soit
)p(i.)p( 22
β
=Φ et donc β
Φ
+= )p( ).p.LR()p(V).p(G 2
2mH
- En utilisant l’ensemble des équations précédentes, on peut faire apparaître la structure du système bouclé
suivant :
On a donc la relation