Sixième partie

Bulletin de la Société Astronomique du Valais Romand Page 12
________________________________________________________________________________
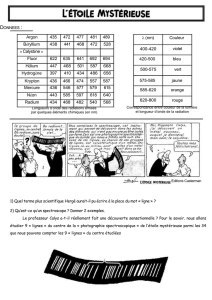
Une application moderne très importante de la spectro-
métrie consiste en la détection des exoplanètes.On ex-
ploite le fait que si une planète tourne autour de son
étoile, elle « induit » également un mouvement de l’é-
toile elle-même (voir le dessin à gauche). C’est un fait
bien connu : lors du lancer du marteau, non seulement
le marteau tourne mais l’athlète aussi tourne autour
d’un point que les physiciens appellent centre de masse
du système « athlète-marteau ». L’athlète étant plus
massif que le marteau, on constante que l’athlète tourne
moins vite que le marteau, heureusement ! Pareillement
en astronomie le système « étoile-planète » tourne au-
tour de son centre de sa masse : ce dernier se trouve
bien sûr très proche du centre de l’étoile car l’étoile est
bien plus massive que n’importe quelle planète. L’étoile
tourne ainsi bien moins vite que la planète, malheureu-
sement pour la mesure !!
Introduction à la spectrométrie
Sixième partie : détection d'exoplanètes par la mesure de la vitesse radiale par Alain Kohler
L'effet Doppler sonore
Quand une sirène s'approche de nous, passe devant nous puis
s'éloigne de nous, on entend au moment du passage une brus-
que chute de la hauteur du son. Le physicien autrichien Dop-
pler a, au début du XIXème siècle, expliqué ce phénomène
via la nature ondulatoire du son.
Considérons une source sonore fixe et un observateur (une
oreille !) fixe. La source émet un son à une certaine fré-
quence. Compte tenu de la vitesse du son, vson, déterminée
par le milieu (l'air), la source impose donc une certaine lon-
gueur d'onde λs au son. On représente donc cette longueur
d'onde sur le graphique (à droite) par la distance qu'il existe
entre deux fronts d'onde. Nous appelons cette longueur
d'onde par λréelle.
Comme les planètes sont encore très difficilement détecta-
bles en direct, on s’attelle à détecter le mouvement induit
sur leur étoile. Ceci peut se réaliser grâce à l’effet Doppler.
Si maintenant la source se déplace en direction de
l'observateur à la vitesse vsource, on constate un rap-
prochement des fronts d'onde c'est-à-dire que la lon-
gueur d'onde diminue de la distance parcourue par la
source vsourceTréelle, où Tréelle est le temps séparant l’é-
mission de deux fronts d’onde par la source. La nou-
velle longueur d'onde perçue par l'observateur, qu'on
va appeler longueur d'onde apparente vaut alors :
λapp = λréelle - vsourceTréelle
Or la vitesse du son (de l’onde) est donnée par :
vson = λréelle / Tréelle
Source fixe
Source mobile

Bulletin de la Société Astronomique du Valais Romand Page 13
________________________________________________________________________________
En combinant ces deux dernières équations, on
obtient :
λréelle - λapp = Vsource
__ Vson λréelle
Dans le cas traité, la source se rapproche de l'observa-
teur ce qui se traduit par une diminution de la lon-
gueur d'onde : physiologiquement, cela s'entend par un
son plus haut que celui émis par la source. On a la si-
tuation opposée quand la source s'éloigne de l'observa-
teur, la longueur d'onde apparente est plus grande et
cela s'entend comme un son perçu plus grave.
L'effet Doppler en astronomie
On retrouve ce même effet avec la lumière car celle-ci
est, comme le son, une onde. Si on considère une
source de lumière en mouvement par rapport à un ob-
servateur, on obtient la même formule que précédem-
ment. La différence entre la vraie longueur d'onde et
celle mesurée (apparente) se notant par ?? et la vitesse
de l'onde est celle de la lumière soit c, on obtient
alors :
vsource = Δλ
c λ
Un changement de longueur d'onde se traduit par un
changement de couleur. Une étoile nous envoie un
spectre discret d'absorption superposé à un spectre
continu. Lorsque l'étoile s'éloigne de nous, tout le
spectre est décalé vers des longueurs d'onde plus
grandes (on parle par image d'un décalage vers le
rouge ou redshift, langage quelque peu abusif si on
pense que la couleur rouge va elle se décaler vers l'in-
frarouge). Concernant le spectre continu, on ne verra
pas de différence, puisque toutes les couleurs seront
représentées à nouveau. Par contre les lignes du spec-
tre d'absorption sont liées à des longueurs d'onde bien
précises (éléments chimiques) : un décalage de celles-
ci traduit donc une vitesse de la source.
Etoile immobile par
rapport à l'observa-
Etoile mobile par rap-
port à l'observateur
Il est important de noter que la formule précédente
donne une relation de proportionnalité entre la diffé-
rence de longueur d'onde mesurée et la vitesse de
l'étoile qu'on veut déterminer.
Donc plus cette différence en longueur d'onde est
grande, plus la vitesse de l'étoile est élevée.
Concrètement, on relève avec un spectromètre le
spectre d'une étoile qu'on compare avec un spectre
terrestre de référence pour la calibration des lon-
gueurs d'onde. Si l'on constate que les raies d'absorp-
tion (ou d'émission par exemple pour une nébuleuse)
ne sont pas au bon endroit, cela traduit une vitesse de
la source par rapport à l'observateur.
Il faut encore préciser que cette technique permet de
mesurer une vitesse liée à un rapprochement ou à un
éloignement : on parle de vitesse radiale (selon le "
rayon " ou distance variable nous séparant de l'étoile).
Cette technique ne permet pas de mesurer une vitesse
transversale (étoile se déplaçant à distance constante
de nous) : de manière générale, la vitesse d'une étoile
est la combinaison des deux mais seule la vitesse ra-
diale est mesurable par l'effet Doppler.

Bulletin de la Société Astronomique du Valais Romand Page 14
________________________________________________________________________________
Application de l'effet Doppler aux exoplanètes
L'effet Doppler a d'abord été appliqué pour la mesure de la vitesse radiale d'étoiles doubles. Au cours du temps, on
relève que la longueur d'onde augmente puis diminue, ceci de manière périodique, ce qui traduit un mouvement de
rapprochement et d'éloignement engendré par la révolution des étoiles autour de leur centre de masse.
A
B
La technique utilisée pour la détection des
exoplanètes est strictement la même à un détail
expérimental important près : la vitesse de l’étoile
autour de laquelle tourne l’exoplanète est très faible
par rapport à une étoile double. Pour illustrer ceci,
prenons la situation du système Terre-Soleil (on fait
abstraction ici des influences des autres planètes…).
La Terre se déplace à une vitesse d’environ 30 km/s
autour du Soleil. Le Soleil est 300'000 fois plus
massif que notre planète. En conséquence, la vitesse
du Soleil imputable au mouvement de la Terre est
300'000 fois plus faible, ce qui correspond à
seulement 0,1 m/s. Un être humain au pas va dix fois
plus vite !
Ainsi pour mesurer un système équivalent au système
Terre-Soleil, il faudrait un sepctromètre capable de
détecter 0,1 m/s ( = vitesse de la source)
comparativement à la vitesse de la lumière ( = vitesse
de l’onde) qui est de 300 millions de m/s. On doit
donc avoir le même rapport pour la différence de
longueur d’onde constaté comparée à la longueur
d’onde de référence. Autrement dit une résolution de
3 milliards !! Inimaginable !!
Et pourtant… lorsque l’équipe franco-suisse, avec
Michel Mayor et Didier Queloz., découvre la
première exoplanète, 51 Pegasus, en 1995,
l’incertitude sur les vitesses n’est même pas de
10 m/s ! Le graphique ci-dessous traduit bien un
mouvement périodique d’aller-retour de l’étoile, donc
en principe, de la planète qui lui est jointe.