Traitement des requêtes Top-K sur une base de données

Traitement des requêtes Top-K sur une base de données
crédibiliste
Top-K queries for evidential databases
Salma Ben Harrath
Université de Tunis
IRISA
LARODEC
[email protected]
Arnaud Martin
Université de Rennes
IRISA
Arnaud.Martin@univ-
rennes1.fr
Boutheina BenYaghlane
Université de Carthage
LARODEC
Boutheina.Y[email protected]nu.tn
ABSTRACT
L’interrogation de bases de donn´ees contenant des informa-
tions impr´ecises soul`eve diff´erents probl`emes, dont celui de
la mod´elisation. Dans ce papier, nous nous int´eressons `a
la d´efinition d’un score pour les bases de donn´ees pouvant
contenir des valeurs mal connues ou incertaines repr´esent´ees
par la th´eorie des fonctions de croyance. Les requˆetes consid-
´er´ees, dites cr´edibilistes, sont assez diff´erentes d’autres types
de requˆete: l’utilisateur n’a qu’`a exprimer ses pr´ef´erences
sous forme d’id´ees qui sont parfois complexes. Notre ob-
jectif est de lui fournir les Top-K meilleurs r´eponses en se
basant sur une distance de smilarit´e qui calcule le degr´e
d’appartenance des conditions de la requˆete aux attributs
cr´edibilistes pr´esent´es sous forme de distributions de masse
dans la base de donn´ees.
Keywords
base de donn´ees cr´edibiliste, requˆete cr´edibiliste, score.
ABSTRACT
Querying databases containing imprecise information raises
various problems, including modeling. In this paper, we fo-
cus on defining a scoring function for databases that can
contain ill-known values or uncertain values represented by
the theory of belief functions. The framework chosen to
model the data is that of evidential databases; The consid-
ered queries, say credebilistic ones, are quite different from
other types of queries: “we do not know what we seek, what
is expecting as a result”. In this paper, we show the value
of introducing a method based on the computation of the
distance between the query and credebilistic attribute ex-
isting into databases to aggregate its similarity. Finally, we
organize those scores in order to present the Top-K results
responding to user preferences.
Keywords
Evidential database, evidential query, Evidential attribute,
score.
1. INTRODUCTION
Les bases de donn´ees constituent un domaine de l’informatique
consacr´e `a la manipulation et le stockage de grandes quan-
tit´es d’informations. Une base de donn´ees repr´esente ainsi
l’image informatique des donn´ees relatives `a un univers r´eel.
De nos jours et avec l’´emergence des applications sur le web
telles que les r´eseaux sociaux, les serveurs web, le commerce
´electronique, des incertitudes et des impr´ecisions sur les don-
n´ees acquises apparaissent fr´equemment dans les bases de
donn´ees.
Face `a ces imperfections, plusieurs actions s’offrent `a nous :
soit nous tentons de les supprimer, ce qui n´ecessite une com-
pr´ehension, souvent difficile, des sources qui ont conduit `a
ces imperfections ; soit nous cherchons `a d´evelopper des pro-
cessus de traitement robustes `a ces imperfections ; soit nous
cherchons `a les mod´eliser.
Dans de nombreuses applications telles que celles li´ees `a in-
ternet, il est important de pouvoir mod´eliser les bases de
donn´ees complexes contenant des donn´ees incertaines eux-
mˆemes complexes. Une mod´elisation concr`ete et fine de
donn´ees mal connues peut ˆetre r´ealis´ee `a l’aide des th´eories
de l’incertain telles que la th´eorie des probabilit´es [2, 7], la
th´eorie des possibilit´es [6, 9] ou encore la th´eorie des fonc-
tions de croyance [12, 14].
En effet l’incertitude sur les donn´ees engendre de nombreuses
s´emantiques possibles `a l’´egard par exemple des requˆetes
top-k. Ces requˆetes, qui nous int´eressent particuli`erement,
permettent de pr´esenter diff´erents tuples ordonn´es r´epon-
dant au mieux `a la requˆete. En pr´esence des s´emantiques
d’un monde possible, chaque base de donn´ees incertaine peut
ˆetre vue comme un encodage succinct d’une distribution sur
les mondes possibles. Chaque monde possible est une table
relationnelle (des donn´ees certaines) sur laquelle nous pou-
vons ´evaluer la requˆete top-k de fa¸con traditionnelle [21].
Dans ce papier, nous d´efinissons une fonction de score sur
une base de donn´ees cr´edibiliste qui peut ˆetre employ´ee par
la m´ethode des top-k.
Cet article est pr´esent´e comme suit, la section 2 permet

de rappeler la d´efinition des bases de donn´ees impr´ecises
et incertaines et d’expliquer le choix des bases de donn´ees
cr´edibilistes et l’inf´erence des requˆetes cr´edibilistes. En effet,
dans cette section, nous pr´esentons le principe de top-k et ses
avantages ce qui nous m`ene `a la section 3 o`u nous d´ecrivons
le processus adapt´e pour mod´eliser les attributs cr´edibilistes
en utilisant la fonction de score avant de l’illustrer et finale-
ment conclure.
2. LES BASES DE DONNÉES IMPRÉCISES
ET INCERTAINES
Les informations existantes dans les bases de donn´ees peu-
vent ˆetre `a la fois incertaines (admettent une composante
al´eatoire), impr´ecises (pas assez focalis´ees) ou incompl`etes
(ayant un point de vue partiel).
Ainsi dans une base de donn´ees impr´ecise et incertaine, cer-
taines valeurs d’attribut sont mal connues et repr´esent´ees
par des ensembles disjonctifs pond´er´es [6], c’est-`a-dire par
des probabilit´es, des possibilit´es ou des fonctions de masses
selon le cadre th´eorique choisi pour mod´eliser les imperfec-
tions. Au del`a de la diff´erenciation des types de bases de
donn´ees, un aspect important concerne la mod´elisation de
telles bases de donn´ees est mis en ´evidence.
Pour aborder ce probl`eme, des bases de donn´ees cr´edibilistes
ont ´et´e propos´ees par [1, 23]. La th´eorie des fonctions de
croyance [25, 26, 24] est class´ee parmi les approches les plus
capables de repr´esenter, g´erer les donn´ees incertaines et im-
pr´ecises mais aussi de mod´eliser l’ignorance.
En premier lieu, la th´eorie des fonctions de croyance permet
de repr´esenter les donn´ees impr´ecises, incertaines et gradu-
elles que d’autres approches savent g´erer. Elle offre en effet
un cadre formel solide pour le traitement de l’incertitude
(notion prise dans son acception la plus large).
D’autre part, la th´eorie des fonctions de croyance supporte
le m´ecanisme de mise en conformit´e des n-uplets vis-`a-vis
des connaissances de domaine. En effet, ces connaissances
de domaine, d´efinies par une collection de mondes possibles,
d´elivrent un vocabulaire contrˆol´e qui sert `a d´ecrire les re-
quˆetes dans un langage proche de celui de l’utilisateur. En-
fin, la base de donn´ees cr´edibiliste offre une interface sym-
bolique pour mod´eliser des donn´ees cr´edibilistes avec des
fonctions de masses.
Pour interroger une telle base de donn´ees, nous d´efinissons
des requˆetes, dites cr´edibilistes. Ces requˆetes cr´edibilistes
correspondent `a des requˆetes impr´ecises pour lesquelles
l’utilisateur lui-mˆeme a des doutes (incertitude). Par ex-
emple, lors d’une recherche sur le web, l’utilisateur ne sait
pas toujours quels mots cl´es il doit saisir pour r´epondre `a
un besoin/concept qu’il ne sait lui mˆeme pas d´efinir. Les
requˆetes cr´edibilistes sont consid´er´ees comme ´etant des re-
quˆetes complexes (c’est-`a-dire des requˆetes de haut niveau).
2.1 Utilité des requêtes Top-K
Nous nous int´eressons aux requˆetes Top-k pour les adapter
avec une base de donn´ees cr´edibiliste. ce type de requˆetes
pr´esentent deux avantages principaux :
•Premi`erement, Les requˆetes Top-k offrent la possibilit´e
aux utilisateurs de qualifier les r´esultats d’une requˆete
grˆace `a une fonction de score. Elles permettent aux
utilisateurs de qualifier les r´esultats de leurs requˆetes
par rapport aux donn´ees existantes dans les bases de
donn´ees ceci en fonction de leurs pr´ef´erences person-
nelles. Ce type de requˆetes permettra donc aux utilisa-
teurs des applications sur le web de pouvoir rechercher
des donn´ees en fonction de leurs pr´ef´erences person-
nelles au lieu d’une simple recherche par identifiant ou
par une cl´e (exact match) qui ne pourra pas leur per-
mettre d’´evaluer la qualit´e d’une r´eponse par rapport
`a une autre.
•Deuxi`emement, elles ´evitent de submerger les utilisa-
teurs avec un grand nombre de r´eponses. Les requˆetes
fournies par l’utilisateur permettent de trier les r´esul-
tats par rapport `a ses propores pr´ef´erences.
Les requˆetes Top-k permettent ´egalement `a l’utilisateur
de limiter le nombre de r´esultats que le syst`eme doit lui
retourner. Les r´esultats retourn´es `a l’utilisateur sont
les meilleurs par rapport `a une fonction de score.
2.2 Base de données probabiliste
Une base de donn´ees probabiliste contient des attributs dont
les valeurs sont mal connues et repr´esent´ees par des distri-
butions de probabilit´e. Une telle base de donn´ees peut ˆetre
interpr´et´ee comme un ensemble de tuples contenant des at-
tributs probablement r´ealisables dans le monde r´eel. Ce type
de base de donn´ees est appropri´e pour capturer l’incertitude
mais il est incapable de mod´eliser l’ignorance totale tant
qu’il ne tient pas compte du cas de l’ensemble vide [14, 17,
19, 20].
Table 1: Probabilistic Database
Patient Age Maladie
Robert [20,25] anemia
Celina 41 0.7 flu, 0.3 cancer
Steve 0.5 cholera, 0.5 anemia
L’exemple suivant en tableau 1 permet d’expliquer que l’attribut
maladie peut ˆetre pr´esent comme une distribution de prob-
abilit´e avec des valeurs incertaines (0.7 flu, 0.3 cancer).
2.3 Base de données possibiliste
Une base de donn´ees possibiliste contient des attributs dont
les valeurs sont mal connues et repr´esent´ees par des dis-
tributions de possibilit´e. L’incertitude d’un ´ev´enement, au
contraire des probabilit´es, est donc caract´eris´ee par deux
valeurs : sa possibilit´e et sa n´ecessit´e. Une telle base de don-
n´ees peut ˆetre interpr´et´ee comme un ensemble de bases de
donn´ees usuelles (encore appel´ees mondes), chacune d’entre
elles ´etant plus au moins possible [10]. Ce type de base
de donn´ees a cependant des limitations de mod´elisation et
de repr´esentation des donn´ees incertaines. La structure des
bases de donn´ees usuelles rend indispensable la pr´esentation
de toutes les possibilit´es d’un attribut en g´en´erant les dif-
f´erents mondes possibles en se basant sur les axiomes des
deux mesures (la necessit´e N, et la possibilit´e Π), ceci en-
gendre des difficult´es au niveau du processus d’interrogation
et du calcul des scores.

Table 2: Possibilistic Database
Patient Age Maladie
Robert [20,25] anemia
Celina 0.7 flu, 1 cancer
Steve 17 cholera
L’exemple donn´e dans le tableau 2 permet d’expliquer que
l’attribut maladie peut ˆetre pr´esent comme une distribution
de possibilit´e avec des valeurs possibilistes (0.7 flu, 1 cancer).
2.4 Base de données crédibiliste
Une litt´erature a ´et´e consacr´ee `a la comparaison des dif-
f´erentes th´eories de l’incertain. Au d´el`a des diff´erences par-
fois subtiles d’interpr´etation, il apparaˆıt pourtant bien dif-
ficile de conclure sur la sup´eriorit´e de l’une ou l’autre des
th´eories pr´esent´ees. Il est clair en tout cas que les objets
math´ematiques manipul´es sont proches et que la th´eorie
des fonctions de croyance peut ˆetre consid´er´ee comme plus
g´en´erale que celle des probabilit´es ou des possibilit´es. Elle
englobe les cas particuliers de ces deux th´eories.
Prendre en compte une base de donn´ees cr´edibiliste permet
ainsi d’avoir une mod´elisation plus compl`ete et moins con-
trainte des informations donn´ees `a la base. Une base de don-
n´ees cr´edibiliste contient des attributs dont les valeurs sont
mal connues et repr´esent´ees par des fonctions de masse. Une
telle base de donn´ees peut ˆetre interpr´et´ee comme un ensem-
ble de propositions qui peuvent correspondre `a la r´eponse
d’une requˆete cr´edibiliste.
Table 3: Base de donn´ees cr´edibiliste
Patient Age Maladie
Robert jeune anemia
Celina 24 0.7 (flu or cancer),
0.3 cancer
Steve [12.25 ] cancer
L’exemple de la base de donn´ees cr´edibiliste du tableau 3
permet d’expliquer que l’attribut maladie peut ˆetre pr´esent
comme une fonction de masses avec des valeurs incertaines
et impr´ecises (0.7 (flu ou Cancer), 0.3 cancer).
Notion de base de la th´eorie des fonctions de croy-
ances
Nous pr´esentons ici quelques concepts de base de cette th´eorie.
Au niveau cr´edal, il est prioritaire de d´efinir un cadre de
discernement ou un univers de discours dit Ω qui sert `a
repr´esenter les ´etats possibles d’un probl`eme donn´e.
Soit Ω = {ω1, ω2,...,ωn}un ensemble fini repr´esentant
toutes les hypoth`eses possibles identifi´ees
ωi(avec i∈ {1,2,...,n}), ou ´etats, que peut prendre un
attribut. Une fonction de masse est d´efinie sur l’ensemble
de tous les sous-ensembles possibles de Ω, not´e 2Ωet affecte
`a chaque sous-ensemble une valeur entre 0 et 1 exprimant
une croyance ´el´ementaire. La fonction de masse not´ee mΩ
ou simplement mest d´efinie par :
mΩ: 2Ω→[0,1] (1)
On impose aussi en g´en´eral m(∅) = 0 qui permet de rester en
monde ferm´e. Les parties Ade Ω telles que m(A)≥0 sont
appel´ees ´el´ements focaux de m. Une masse m(A) repr´esente
ainsi le degr´e de croyance ´el´ementaire attribu´e `a la propo-
sition Aqui, compte tenu de la connaissance `a un moment
donn´e, n’a pas pu ˆetre affect´ee `a un sous-ensemble plus sp´e-
cifique.
La fonction de masses mΩdoit v´erifier les conditions suiv-
antes :
X
A⊆Ω
m(A) = 1 (2)
3. DÉFINITION D’UN SCORE SUR UNE BASE
DE DONNÉES CRÉDIBILISTE
La plupart des syst`emes s’appuie sur l’hypoth`ese que les
r´esultats affich´es en ordre Top-k ont ´et´e parfaitement recon-
nus ou identifi´es et de fait leur fonction de correspondance
s’appuie sur une capacit´e `a disposer d’une relation d’´egalit´e
ou d’appartenance entre les conditions de la requˆete et les
attributs existants dans les tuples de la base de donn´ees.
Aucune tentative n’a ´et´e propos´ee pour int´egrer cette fonc-
tion de score allou´ee au top-k sur des bases de donn´ees cr´edi-
bilistes qui fait l’objet de ce papier. Par ailleurs, il y a tr`es
peu de travaux sur le traitement des requˆetes top-k sur les
bases de donn´ees probabilistes sur des donn´ees incertaines
[3, 4, 5].
Une base de donn´ees cr´edibiliste doit contenir au moins
un attribut cr´edibiliste qui prendra des valeurs cr´edibilistes
d´ecrites par une fonction de masse au lieu d’une valeur cer-
taine et pr´ecise. Nous formalisons l’adaptation de ce score
pour influencer le fait de trouver une fonction d’appartenance
des attributs cr´edibilistes d´ej`a repr´esent´es par des fonctions
de masse par rapport aux conditions de la requˆete Qpro-
pos´ee par l’utilisateur r´epondant `a ses pr´ef´erences person-
nelles.
La fonction de score sp´ecifie `a quel point chaque donn´ee ex-
istante dans les bases de donn´ees correspond aux conditions
de la requˆete. Les fonctions d’appartenance permettent de
d´ecrire une appartenance cr´edible `a une requˆete. Notre pro-
cessus est organis´e comme suit :
Nous consid´erons donc avoir une requˆete Q´emise par l’utilisateur.
Cette requˆete est dite cr´edibiliste constitu´ee par des condi-
tions complexes ou dites aussi cr´edibilistes.
Prenons comme exemple :
Select patient,age from Table 3 where

(mΩmaladie {cancer}>0.3) .
Dans cet exemple, nous sommes en face `a une condition
complexe ou dite cr´edibliliste . Pour trouver les kmeilleurs
r´eponses pour cette requˆete, notre m´ethode r´esout le prob-
l`eme en utilisant les techniques sp´ecifiques de la th´eorie des
fonctions de croyance. Apr`es avoir ex´ecut´e cette requˆete,
on traite les attributs cr´edibilistes existants dans une base
de donn´ees cr´edibiliste qui correspondent aux r´esultats de
recherche de cette requˆete ´emise par l’utilisateur et qui sont
mod´elis´es par des fonctions de masses.
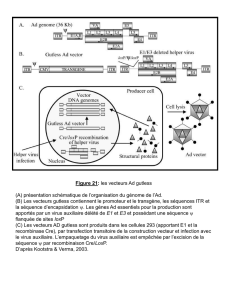
Figure 1: Une mod´elisation des attributs cr´edi-
bilistes
Prenons l’exemple de la requˆete qu’on a d´ej`a ex´ecut´e, le
cadre de discernement de l’attribut ”‘maladie”’ est :
Ωmaladie={anemia, f lu, cancer}.
La fonction de masse attribu´ee `a l’attribut maladie dans
notre exemple, d´ej`a pr´esent´e dans le tableau 3 : le patient
“Celina” a croyance ´el´ementaire d’avoir la maladie (cancer)
est de 0.3 et 0.7 d’avoir (cancer ou flu).
Nous avons donc une fonction de masse donn´ee par la re-
quˆete cr´edibiliste et un ensemble de fonctions de masse cor-
respondant `a l’attribut consid´er´e dans la requˆete. Afin de
d´efinir un score pour appliquer un ordonnancement de k
meilleures r´eponses `a la requˆete, nous proposons d’´etudier
la similarit´e de la fonction de masse issue de la requˆete avec
celles de la base de donn´ees cr´edibiliste.
Il existe plusieurs types de mesures de distances entre deux
fonctions de croyance, la plus utilis´ee est celle propos´ee par
[22] car elle permet de pond´erer les croyances ´el´ementaires
sur les ´el´ements focaux impr´ecis. En effet, la distance de
Jousselme est fond´ee sur la dissimilarit´e de jaccard: |ATB
ASB|
qui tient compte implicitement de la structure des fonctions
de croyance.
La distance de Jousselme est donn´ee pour deux fonctions de
masse m1et m2par :
d(m1, m2) = r1
2(m1−m2)tD(m1−m2),(3)
o`u Dest une matrice 2|Θ|×2|Θ|dont les ´el´ements sont :
D(A, B) = 
1,if A=B=∅,
|A∩B|
|A∪B|,∀A, B ∈2Θ.
(4)
Dcorrespond `a une matrice de similarit´e entre les ´el´ements
focaux, dont les valeurs sont issues de la mesure de Jaccard
entre les sous-ensembles d’´etats correspondants.
Nous notons mΩa
rla fonction de masse de la requˆete li´ee `a
l’attribut aet Ma
b={mΩa
t, t ∈ {T }} l’ensemble des fonc-
tions de masse mΩa
tde la base de donn´ees li´ees `a l’attribut
aet au tuple t. L’ensemble des tuples est not´e T. Nous
devons ainsi calculer l’ensemble des distances d(mΩa
r, mΩa
t)
pour tout t∈ {T }. Nous d´efinissons le score stpar cette dis-
tance. Ce score correspond donc `a la proximit´e d’un tuple
`a la requˆete.
Si la requˆete porte sur plusieurs attributs, nous construisons
autant de fonctions de masse, par exemple mΩa1
ret mΩa2 r
pour deux attributs. Prenons comme exemple :
Select patient,age from Table 3 where
(mΩmaladie (cancer)>0.3) and (mΩage (jeune) = 0.7)
Le score est alors d´efini pour naattributs par :
st=1
na
na
X
i=1
d(mΩai
r, mΩai
t) (5)
Consid´erons `a pr´esent le cas o`u la requˆete comporte sur le
mˆeme attribut, mais avec une condition multiple, par exem-
ple :
SELECT patient,age from Table 3 WHERE
(mΩmaladie (cancer)>0.3) and (mΩmaladie (f lu) = 0.2).
Dans ce cas la mˆeme approche que celle pr´esent´ee ci-dessus
pour plusieurs attributs peut ˆetre employ´ee. Nous pouvons
cependant combiner ces fonctions de masse avec les outils de
la th´eorie des fonctions de croyance. En effet, consid´erant ces
deux conditions comme ind´ependantes, les deux fonctions de
masse que nous notons mΩa
c1et mΩa c2. La fonction de masse
r´esultante de la combinaison conjonctive de Dempster est
donn´ee par :
mΩa
r=1
1−kX
A∩B=X
mΩa
c1(A)mΩa c2(B),(6)
o`u k=X
A∩B=∅
mΩa
c1(A)mΩa c2(B). Le score est ensuite calcul´e

`a partir de la distance comme pr´ec´edemment.
4. ILLUSTRATION
Nous proposons d’illustrer notre approche en consid´erant
qu’il est prioritaire de fournir `a l’utilisateur les kr´esultats
r´epondant au mieux `a ses pr´ef´erences. Ces pr´ef´erences sont
exprim´ees sous forme de requˆetes cr´edibilistes c’est-`a-dire
par des distributions de masse.
L’allocation de masse r´ealis´ee pour la requˆete est construite
`a partir du nombre de conditions ´emises par l’utilisateur.
Ces conditions sont parfois incertaines, impr´ecises ou mˆeme
illisibles.
La cr´eation de la fonction de masse li´ee `a une requˆete d´epend
du type de condition.
Si la condition de la requˆete est exacte prenons l’exemple
suivant :
Select patient,age from Table 3 where
(mΩmaladie {cancer}= 0.3) .
La fonction de masse aura pour seuls ´el´ements focaux {cancer}
et Ωmaladie. La masse associ´ee `a Ωmaladie est alors 0.7.
Si la condition de la requˆete n’est pas exacte c’est-`a-dire ex-
prime la sup´eriorit´e ou l’inf´eriorit´e prenons l’exemple suiv-
ant : Select patient,age from Table 3 where
(mΩmaladie {cancer}>0.3).
Dans ce cas les ´el´ements focaux restent {cancer}et Ωmaladie ,
mais la masse associ´ee `a ces ´el´ements peut ˆetre rerp´esent´ee
sous forme d’intervalle. Ainsi mΩmaladie {cancer}=]0.3,1]
et mΩmaladie (Ωmaladie) = 1 −mΩmaladie {cancer}.
Table 4: Une base de donn´ees contenant des at-
tributs totalement cr´edibilistes
Patient Age Maladie
Refka 24 0.7 (flu or cancer),
0.3 cancer
Salma [28 32] 0.8 (flu or cancer),
0.2 flu
Steve 0.5 (flu or cancer),
0.4 cancer
0.1 Ωmaladie
Andro jeune 0.3 (flu or cancer),
0.3 cancer
0.1 flu
0.3 Ωmaladie
Afin d’illustrer notre approche, nous consid´erons la base
de donn´ees contenant des attributs totalement cr´edibilistes
pr´esent´ees dans le tableau 4 et nous consid´erons la requˆete
cr´edibiliste suivante :
Select patient,age from Table 3 where
(mΩmaladie {cancer}= 0.3).
Le cadre de discernement est toujours
Ωmaladie={anemia, f lu, cancer}. Les seuls ´el´ements focaux
consid´er´es dans la base sont :
{cancer},{flu},{flu, cancer},Ωmaladie. Le tableau 5
pr´esente les fonctions de masse des tuples et de la requˆete.
Par exemple la distance entre la fonction de masse de la re-
quˆete et la fonction de masse du tuple 1 est 0.4041. Ainsi
`a la requˆete correspondant `a une pr´ef´erence d’avoir les tu-
ples dont les patients sont vraissemblablement pas atteint de
cancer (avec une croyance de 0.3) l’ordre des tuples sur la
base de donn´ees exemple est : Salma (tuple 2), Refka (tuple
1), Steve (tuple 3) et Andro (tuple 4).
Table 5: D´efinition des scores dans une base de don-
n´ees cr´edibiliste
requˆete Refka Salma Steve Andro
cancer 0.3 0.3 0 0,4 0.3
flu 0 0 0.2 0 0.1
cancer ∪flu 0 0.7 0.8 0.5 0.3
Ωmaladie 0.7 0 0 0.1 0.3
Score 0.4041 0.4899 0.3391 0.2273
5. CONCLUSION
L’int´erˆet de la th´eorie des fonctions de croyance r´eside dans
sa capacit´e `a mod´eliser des connaissances. C’est donc na-
turellement que nous nous sommes tourn´es vers ce cadre
th´eorique pour aborder le probl`eme complexe du stockage
et de l’interrogation de donn´ees incertaines et impr´ecises. Si
les bases de donn´ees cr´edibilistes ont d´ej`a ´et´e introduites,
nous avons introduit le concept de requˆete cr´edibiliste. Ce
type de requˆete permet `a l’utilisateur d’interroger une base
de donn´ees avec une demande impr´ecise et sans ˆetre sˆur de
ce qu’il recherche.
L’objectif du papier est d’introduire la d´efinition d’un score
dans le contexte de base de donn´ees cr´edibiliste, afin par
exemple d’appliquer une m´ethode top-kdes kr´eponses or-
donn´ees correspondant le mieux `a une requˆete. Une fois les
donn´ees et la requˆete (qui peut ˆetre multi-condition) mod-
´elis´ees par une fonction de masse, nous proposons de d´efinir
ce score `a partir d’une distance entre les fonctions de masse.
L’ordonnancement des scores fournit ensuite le top-k.
Divers travaux futurs sont `a mener, par exemple, il serait
int´eressant d’´etudier l’impact du choix des conditions de la
requˆete sur le nombre des r´eponses que le syst`eme peut af-
ficher.
6. REFERENCES
[1] M-A. BachTobji, B. Ben Yaghlane, and K. Mellouli (2008).
A new algorithm for mining frequent itemsets from
evidential databases. In Information Processing and
Management of Uncertainty, Malaga, Spain, pages
1535-1542.
[2] D. Barbara, H. Garcia-Molina, and D. Porter (1992). The
managementof probabilistic data. IEEE Trans. Knowl. Data
Eng 4(5), pages 487-502.
[3] M-A. Soliman, M. Saleeb, I-F. Ilyas (2010): MashRank:
Towards uncertainty-aware and rank-aware mashups. ICDE,
pages 1137-1140.