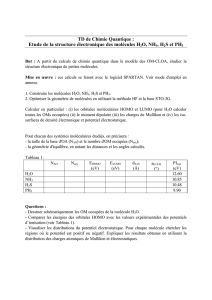
corrigé

Spé y 2008-2009 page 1/7 Devoir n°4
Spé y 2008-2009 Devoir n°4
CHIMIE INORGANIQUE ET PHYSIQUE
CHIMIE
MINES PSI 2007
1. Avec Z = 29, la configuration électronique attendue d’après les règles de Klechkowsky et
de Hundt est: 1s2 2s2 2p6 3s2 3p6 4s23d9.
2. La configuration électronique réelle est 1s2 2s2 2p6 3s2 3p6 3d10 4s1 ce qui assure le rem-
plissage total de la sous-couche 3d : les sous-couches totalement remplies et celles à remplies à
moitié ont une stabilité particulière.
3-a) Le nombre d’atome appartenant à la maille est 8´1/8 + 6´1/2 = 4 atomes.
b) On a r =
m
V
M
a
=
4
3
N. A.N.
( )
3
1223
3
10.5,36110.023,6
10.5,63.4
-
-
=r = 8,92´103 kg.m–3.
4) L’ion Cu+ correspond à la perte d’un électron. Le plus facile est celui de la sous-couche
4s donc la configuration électronique de Cu+ est : 1s2 2s2 2p6 3s2 3p6 3d10 4s0 ;
Pour Cu2+, il y a un électron de moins, le plus facile à enlever est dans la sous-couche 3d
donc la configuration électronique de Cu2+ est : 1s2 2s2 2p6 3s2 3p6 3d9 4s0.
L’énergie de deuxième ionisation est beaucoup plus forte (presque le triple) que celle de
première ionisation car la nature de l’électron arraché change : on doit arracher un électron 3d
d’énergie plus basse que l’électron 4s. Le cuivre est un élément de transition car un de ses ions
(Cu2+) a une sous-couche d incomplète.
5) L’ammoniac NH3 est inchangé de part et d’autre du bilan ; il joue le rôle de ligand.
L’oxygène du dioxygène est à l’état 0 et passe à l’état –II dans OH–. Il joue donc le rôle
d’oxydant.
6) En l’absence d’ammoniac, les ions Cu+ sont oxydants dans le couple
Cu+/Cu(S) de potentiel standard E° = 0,52 V et ils sont réducteurs dans le couple
Cu2+/Cu+ de potentiel standard E° = 0,16 V. D’après la disposition de ces potentiels,
on peut prévoir que les ions Cu+ sont instables en solution aqueuse car ils se dismu-
tent selon le bilan :
2Cu+ = Cu(S) + Cu2+
dont la constante K° est supérieure à un comme le montre le diagramme ci-contre
(“règle du gamma”).
Calcul du potentiel du couple Cu2+ /Cu(S) :
La demi équation du couple Cu2+/Cu+ est Cu2+ + 2e– = Cu(S).
On peut écrire le « cycle d’enthalpie libre ».
On en déduit DrG3° = DrG1° + DrG2°
soit –2FE3° = (–FE1°) – (–FE2°) ou encore E
E
E
3
1 2
2
° =
°+
°
.
A.N. E3
0
16
0
52
2
° =
+
,
,
= 0,34 V.
7) Pour p = 1, on a le bilan de formation du complexe Cu2+ + NH3 = Cu(NH3)2+ qui est
l’inverse du bilan de dissociation globale donc KK
0 1
1
1
,
,
° = °
D
.
Traitons par exemple le cas où p = 2 :
Le bilan de formation du complexe est Cu(NH3)22+ + NH3 = Cu(NH3)32+ avec, par défini-
tion de la constante d’équilibre, DrG°2,3 = –RTln(K2,3°)
E°
0,52 V
0,16 V
Cu
+
Cu
+
Cu(S)
Cu
2+
Cu
2+
+ e
–
= Cu
+
Cu
2+
+ 2e
–
= Cu(S)
Cu
+
+ e
–
= Cu(S)
D
rG°3
D
rG°1
D
rG°2

Spé y 2008-2009 page 2/7 Devoir n°4
Or on a les bilans de dissociation globale :
Cu(NH3)22+ = Cu2+ + 2NH3 avec DrG°D,2 = –RTln(KD,2°)
Cu(NH3)32+ = Cu2+ + 3NH3 avec DrG°D,3 = –RTln(KD,3°)
On a donc la combinaison linéaire DrG°2,3 = DrG°D,2 – DrG°D,3 ce qui conduit à
RTln(K2,3°) = RTln(KD,2°) – RTln(KD,3°)
puis K2,3° = KD,2°/KD,3°.
On généralise cette relation en K
K
K
P P
D P
D P
-
-
° =
°
°
1
1
,
,
,
pour p > 1.
On a donc le tableau
K0,1°K1,2°K2,3°K3,4°
1
10
4 1-= , 104,1 10
10
4 1
7 6
-
-=
,
, 103,5 10
10
7 6
10 5
-
-=
,
, 102,9 10
10
10 5
12 6
-
-=
,
, 102,1
Par définition, pNH3 = –log([NH3/c°). Une valeur élevée de pNH3 correspond donc à une
concentration [NH3] faible.
En notant L le ligand NH3, on peut écrire le bilan CuLP–12+ + L = CuLP2+, la condition
d’équilibre s’écrit Kc
P P
P EQ
P EQ EQ
CuL
CuL L
-
+
-
+
° = °
1
2
1
2
,
[ ]
[ ] donc Kc
P P
EQ P EQ
P EQ
L CuL
CuL
-
+
-
+
°°=
1
2
1
2
,
[ ]
[ ] .
On a donc [ ]
[ ]
CuL
CuL
P EQ
P EQ
2
1
2
1
+
-
+> si K
c
P P
EQ
L
-°
°
>
11 , soit log( ) log ,
Kc
P P
EQ
L
-° + °
F
H
G
I
K
J>
10 ou encore
-°
F
H
G
I
K
J< °
-
log log( )
,
LEQ
P P
cK1. Le domaine de prédominance de CuLP2+ est donc le domaine tel que
pNH3 < log(KP-1,P°) et celui de CuLP–12+ tel que
pNH3 > log(KP-1,P°).
On a donc le diagramme de prédominance suivant :
8) La demi équation du couple
Cu(NH3)42+ / Cu(NH3)2+ est
Cu(NH3)42+ + e– = Cu(NH3)2+ + 2 NH3 avec DrG5° = FE5°.
Avec le bilan Cu(NH3)42+ = Cu2+ + 4 NH3 [DrG°D,4 = –RTln(KD,4°)] et la demi équation re-
dox 4 Cu2+ + e– + 2 NH3 = Cu(NH3)2+ [D
r
G°
6
= –FE6°], on obtient la combinaison linéaire
DrG5° = DrG°D,4 + DrG°6 d’où E
RT
K E
5 4 6
° = ° + °
F
ln( )
,D = ° + °
RT
K E
F
ln( ) log( )
,
10 4 6D .
Par définition, pKD,4 = –log(KD,4°) donc il reste
E
K
E
5 4 6
0
060
°
=
-
+
°
,
.
,
p
D.
A.N
E
5
0
060
12
6
0
82
°
=
-
+
(
,
).
(
,
)
,
= 0,064 V.
9) Pour l’état +I, on ne considère pas l’espèce Cu+ car on a vu qu’elle se dismute ; le cuivre
à l’état + I n’est donc pris en compte que sous sa forme complexée la plus stable : Cu(NH3)2+ .
Pour l’état +II, on ne considère que le complexe
Cu(NH3)p2+ le plus stable à savoir Cu(NH3)42+.
10) Les domaines de prédominance des espèces
d’état redox plus grand sont au-dessus de ceux des es-
pèces d’état redox plus faible.
Pour l’état +II, on a vu que le domaine de pré-
dominance de Cu(NH3)42+ correspond aux faibles va-
leurs de pNH3.
On a donc le schéma ci-contre.
11) Ÿ Frontière (1) : couple Cu(NH3)2+ / Cu(S)
CuL4
2+
CuL3
2+
CuL2
2+
CuL
2+
Cu
2+
pNH3
2,1
2,9
3,5
4,1
Cu(NH
3
)
4
2+
Cu(NH
3
)
2
+
Cu
2+
Cu
(S)

Spé y 2008-2009 page 3/7 Devoir n°4
Cu(NH3)2+ + e– = Cu(S) + 2 NH3
E E c
F
3 F
3 F
Cu(NH
NH
1 4
2 1
1
2
0 06= °+ °
F
H
G
I
K
J
+
, .log [ ) ]
[ ] car a(Cu(S)) = 1. Comme [Cu(NH3)2+]F1 = 1 mol.L–1
par hypothèse, il reste E E
F 3
NH
1 4 0 12= °- , .log [ ]
b
g
soit EF1 = E4° + 0,12pNH3.
Ÿ Frontière (2) : couple Cu(NH3)42+ / Cu(NH3)2+
Cu(NH3)42+ + e– = Cu(NH3)2+ + 2 NH3
E E c
F
3 F
3 F 3
Cu(NH
Cu(NH NH
2 5
4
2
2
2
2 2
2
0 06= °+ °
F
H
G
I
K
J
+
+
, .log [ ) ]
[ ) ] [ ] . Comme [Cu(NH3)2+]F2 = [Cu(NH3)42+]F2, il
reste E E
F 3
NH
2 5 0 12= °- , .log [ ]
b
g
soit EF2 = E5° + 0,12pNH3.
Ÿ Frontière (3) : couple Cu2+ / Cu(NH3)2+
Cu2+ + e– + 2NH3 = Cu(NH3)2+
E E c
F
F 3
3 F
Cu NH
Cu(NH
3 6
2
2
2
2 2
2
0 06= °+ °
F
H
G
I
K
J
+
+
, .log [ ] [ ]
[ ) ] . Comme [Cu(NH3)2+]F3 = [Cu2+]F3, il reste
E E
F 3
NH
3 6 0 12= °+ , .log [ ]
b
g
soit EF3 = E6° – 0,12pNH3.
12) Le dioxygène est oxydant dans le couple O2(G)/H2O. La demi équation est
O2(G) + 4 H+ + 4 e– = 2 H2O
et le potentiel redox E E p
p c
= ° + ° °
F
H
G
I
K
J
+
( / ) ,log ( )[ ]
.
O H O O H
2 2
2
4
4
0 06
4. Comme p(O2) = p°, il
vient E E c = ° - °
F
H
G
I
K
J
+
( / ) , log [ ] O H O H
2 2 0 06 = E°(O2/H2O) – 0,06pH.
À pH = 11, on obtient E = 1,23 – (0,06)(11) = 0,57 V.
La lixiviation correspond à l’oxydation du cuivre (0) pour le faire
passer en solution sous forme de cuivre (II). Si pNH3 = 0 (et pH = 11), la
situation des potentiels est la suivante :
La lixiviation du cuivre par le dioxygène en milieu ammoniacal est
donc tout à fait envisageable.
13) La pyrométallurgie du cuivre correspond au bilan
Cu2O(S) + FeS(S) = Cu2S(S) + FeO(S)
Le système évolue dans le sens direct du bilan si DG > 0. Or le bilan envisagé ne met en jeu
que des solides non miscibles, donc DrG = DrG°.
On calcule DrG° = DrH° – TDrS° avec :
Ÿ DrH° = DfH°(Cu2S(S)) + DfH°(FeO(S)) – [DfH°(Cu2O(S)) + DfH°(FeS(S)) ]
A.N. DrH° = (–80) + (–164) – [(–169) + (–100)] = 25 kJ.mol–1 ;
Ÿ DrS° = Sm°(Cu2S(S)) + Sm°(FeO(S)) – [Sm°(Cu2O(S)) + Sm°(FeS(S)) ]
A.N. DrS° = (121) + (59) – [(93) + (60)] = 27 J.K–1.mol–1 ;
On obtient donc, en kJ.mol–1, DrG°(T) = 25 – 27´10–3.T.
Le système évolue dans le sens direct si DrG°(T) < 0 soit si T > 926 K. À 10% près, on peut
écrire T > 1000 K.
Si on mélange les quatre solides à une température T > 926 K, au moins un des deux réactifs
va disparaître (c’est le réactif limitant). Dans l’état final, on a les deux solides produits (Cu2S et
FeO) et au plus un seul des deux réactifs.
14) Le bilan d’oxydation du sulfure de cuivre est Cu2S(S) + O2(G) = 2Cu(S) + SO2(G).
Le dioxyde de soufre gazeux SO2 coproduit de la réaction peut servir pour la préparation in-
dustrielle de l’acide sulfurique.
E°
0,57 V
–0,15 V
O2(G)
Cu(S)
H2O
Cu(NH3)4
2+
Cu(NH3)2
+
0,06 V
Cu(NH3)2
+

Spé y 2008-2009 page 4/7 Devoir n°4
15) La variance est le nombre de paramètres intensifs que l’on peut choisir indépendamment
pour obtenir un état d’équilibre d’un système réactionnel.
D’après la formule de Gibbs, on a v = c + 2* – j avec :
Ÿ c = 4 – 1 = 3 car on a les espèces Cu2O, Cu2S, SO2 et Cu reliées par le bilan donné ;
Ÿ 2
*
= 2 car, pour le bilan indiqué, DrH° = 0 donc T est facteur d’équilibre et
ai
GAZ
å=1 donc p est facteur d’équilibre ;
Ÿ j = 4 (3 solides non miscibles et un gaz).
Il reste donc v = 1 : le système est monovariant : on ne peut choisir qu’un seul paramètre, p
ou T pour réaliser l’état d’équilibre du système. En travaillant à une pression fixée, il est donc facile
d’éliminer les restes de CuO en se plaçant à une autre température que celle d’équilibre.
16) Dans l’acide nitrique, c’est l’ion NO3– qui est oxydant suivant la demi équation :
NO3– + 4H+ + 3e– = NO(G) + 2H2O.
Le bilan de l’oxydation du cuivre par l’ion nitrate est donc le suivant :
2NO3– + 8H+ + 3Cu(S) = 2NO(G) + 4H2O + 3Cu2+.
17) L’acide nitrique est en excès ce qui permet la consommation totale du cuivre. D’après le
bilan, la quantité initiale de cuivre est 3/2 fois celle de NO produite. Or on obtient n
pV
RT
( )NO =
donc il y avait initialement n
pV
RT
( )Cu =
3
2
soit une masse m
pV
RT
M( ) ( )Cu Cu=
3
2
.
A.N. m( ) ( )( , )
( )( )
Cu =´-
3
2
10 0 04 10
8 300 64
5 3
= 0,16 g.
Si l’échantillon était en cuivre pur il pèserait 0,16 g. Or il pèse 0,18 g : la fraction massique
de cuivre est donc x = 0,16 / 0,18 = 89 %.
PHYSIQUE
BANQUE PT 2007
1-a) On a un conducteur mobile dans un champ magnétique. On attend un phénomène
d’induction de type Lorentz. Si b = 0, le champ magnétique est uniforme donc son flux à travers le
cadre constant. On en déduit que la f.e.m. e est nulle d’après la loi de Faraday
e
d
t
dt
= -
F
(
)
.
On peut calculer la f.e.m. par sa définition e E P P d: ( ). ( )=
z
r
r
l
mt
G
où G
est le contour ABCD orienté indiqué sur la figure.
On a e v P B P d= Ù
z
r
r
r
l( ) . ( )
d
i
t
G
= Ù
z
ve Be P d
r
r
r
l
Z X
b
g
t( )
G
car
r
v
et
r
B
sont
les mêmes en tout point P du contour. On a donc
evBe P d P d P d P d
A
B
B
C
C
D
D
A
= + + +
L
N
M
O
Q
P
z
z
z
z
r
r
l
r
l
r
l
r
l
Yt t t t( ) ( ) ( ) ( ) e vBe P d P d
A
B
C
D
= +
L
N
M
O
Q
P
z
z
r
r
l
r
l
Yt t( ) ( ) car
r
t
est
perpendiculaire à
r
e
Y sur les branches BC et DA. Sur AB,
r
t
=
r
e
Y et sur CD,
r
t
= –
r
e
Y donc il reste
e vB d d
A
B
C
D
= -
L
N
M
O
Q
P
z
z
l l . Comme les brins AB et CD ont la même longueur, on obtient encore e = 0.
La démonstration montre qu’une forme de cadre différente aurait conduit à une f.e.m. non
nulle bien que le flux soit toujours constant.
b) Si b > 0, le module du champ
r
B
diminue lorsque z augmente donc le flux du
champ à travers la surface du cadre orienté comme indiqué sur la figure diminue lorsque le cadre
descend.
y
z
z + a
Ä
r
e
X
O
A B
C
D
G

Spé y 2008-2009 page 5/7 Devoir n°4
D’après la loi de Lenz, le phénomène d’induction tend à s’opposer, par ses effets, à la cause
qui le produit, c’est à dire ici la variation du flux. Pour compenser la diminution du flux, il apparaît
donc dans le cadre un courant qui crée un champ magnétique propre dans le même sens que
r
B
. Le
courant circule donc réellement dans le sens du contour indiqué sur la figure.
c) Par définition, le flux de
r
B
à travers la surface S du cadre orienté comme ci-
dessus est FS
S
=
zz
r
r
B P n P dS( ). ( ) .
On repère le point courant P dans la base cartésienne avec yP Î [0, a], zP Î [z(t), z(t) + a].
Dans cette base, on a dS = dyP.dzP,
r
B
(P) = (B0 – bzP)
r
e
X et
r
n
S =
r
e
X.
Il vient donc F = -
zz
B bz dy dz
0 P P P
b
g
= -
z
z
+
dy B bz dz
a
z t
z t a
P P P
00
b
g
( )
( ) = -
L
N
M
O
Q
P
+
a B z b z
z t
z t a
0
2
2
P
P
( )
( )
= - + -
F
H
G
I
K
J
a B a b z t a z t
0
22
2
( ) ( )
b
g
= - +
F
H
G
I
K
J
a B a b a az t
0
22
2
( ) soit F = - -B a ba ba z t
0
2 3 2
1
2
( ).
D’après la loi de Faraday, la f.e.m. d’induction est alors e
d
t
dt
= -
F
(
)
soit e t ba
dz
t
dt
( )
(
)
=2.
Remarque : comme le cadre tombe, on a
dz
t
dt
(
)
>0 donc e > 0. Comme cette f.e.m. est la
seule présente dans le cadre, elle engendre un courant positif c’est-à-dire circulant réellement dans
le sens du contour ce qui est bien conforme au résultat de la question 1-b. 2-a) On se place dans le
référentiel lié au sol.
2-a) Le système mobile est le cadre en translation.
Il est soumis à :
Ÿ son poids
r
r
P mg= = mg
r
e
Z (avec g > 0) d’après l’orientation de
r
e
Z ;
Ÿ la réaction de la glissière qui n’a pas de composante suivant
r
e
Z puisque l’on néglige
tous les frottements ;
Ÿ la force de Laplace due à la circulation d’un courant i dans le conducteur placé
dans
r
B
. Sur un morceau de longueur dℓ du contour, on a d
r
F
LAP = i(t)
r
t
(P)dℓÙ
r
B
(P). Sur tout le
contour, il vient donc
r
r
r
lF i t P B P d
LAP = Ù
z
( ). ( ) ( )t
G
. On repère le point courant P dans la base carté-
sienne donc
r
r
r
l
r
r
lF i t e P B z t e d e P B z e d
A
B
B
C
LAP Y X Z P X
= Ù + Ù +
L
N
M
z
z
( ) ( ) ( ) ( ) ...
b
g
b
g
... ( ) ( ) ( )+ - Ù + + - Ù
O
Q
P
z
z
r
r
l
r
r
le P B z t a e d e P B z e d
C
D
D
A
Y X Z P X
b
g
b
g
b
g
b
g
.
Comme
r
r
l
r
r
le P B z e d e P B z e d
B
C
D
A
Z P X Z P X
( ) ( )Ù = - - Ù
z
z
b
g
b
g
b
g
, il reste
r
r
r
F i t B z t e a B z t a e a
LAP Z Z
= - + +( ) ( ) ( )
b
g
b
g
b
g
b
g
=
+
-
i t a B z t a B z t e( ) ( ) ( )
b
g
b
g
r
Z
=
-
+
-
+
i t a B b z t a B bz t e( ) ( ) ( )
0 0
b
g
r
Z
soit
r
r
F i t ba e
LAP
Z
= - ( ) 2.
Le théorème de la résultante cinétique appliqué au centre d’inertie G du cadre s’écrit
m
d
v
dt
P R F
r
r
r
r
G
LAP
= + + . Comme le cadre est en translation,
r
v
G(t) = v(t)
r
e
Z. En projection sur
r
e
Z, il
reste m
dv
t
dt
mg i t ba
(
)
( )= - 2.
b) En négligeant le phénomène d’autoinduction, le schéma électrique équi-
valent du cadre est le suivant :
En orientant l’intensité comme la circulation, on obtient e(t) = Ri(t) soit
A B
C
D
R
e(t)
i(t
)