6 Lois des circuits

6. LOIS DES CIRCUITS III. Electricité
6 Lois des circuits
6.1 Circuit série
Considérons le circuit suivant, où deux résistances sont branchées en série à un générateur de
courant :
R1R1
I1
I2
I3
U1U2
Utot.
Figure III.11 – deux résistances en série
6.1.1 Intensité du courant
La charge qui traverse une section du circuit par seconde est la même en tout point du circuit.
L’intensité du courant dans un circuit série est donc la même àtraverstouteslescomposantes
du circuit :
I1=I2=I3=I
6.1.2 Tension
Si une charge de 1Ctraverse la première résistance, elle cède une énergie correspondant à la
tension U1àlarésistanceR1.SicettechargetraverseensuiteR2,elleperduneénergiecor-
respondant à U2.L’énergietotalecédéeparlachargede1Caux deux résistances est donc la
somme des deux énergies échangées.
La tension totale aux bornes de deux composantes, branchées en série, est égale à la somme
des tensions de chacune des composantes :
Utot. =U1+U2
6.1.3 Résistance
On se propose de remplacer deux résistances R1et R2en série par une seule résistance Rtot.,
sans que l’intensité du courant électrique dans le circuit nechange:
110

6. LOIS DES CIRCUITS III. Electricité
R1R1
I
I
I
U1U2
Utot.
Rtot.
I
I
I
Utot.
Figure III.12 – remplacer 2 résistances en série par une seule résistance
Pour la première résistance, la loi d’Ohm s’écrit :
U1=R1·I(1)
Pour la deuxième résistance, la loi d’Ohm s’écrit :
U2=R2·I(2)
Pour la résistance totale, la loi d’Ohm s’écrit :
Utot. =Rtot. ·I(3)
Comme les tensions aux bornes des deux résistances s’additionnent, on a :
Utot. =U1+U2(∗)
En remplaçant (1), (2) et (3) dans (*) :
Rtot. ·I=R1·I+R2·I
après simplification par I, on obtient finalement :
Rtot. =R1+R2
La valeur totale de deux résistances branchées en série est égale à la somme des deux résistances
individuelles.
111

6. LOIS DES CIRCUITS III. Electricité
6.2 Circuit parallèle
Considérons le circuit suivant, où deux résistances sont branchées en parallèle à un générateur
de courant :
R1
R2
I
I1
I2
I1
I2
I
U1
U2
U
BA
Figure III.13 – deux résistances branchées en parallèle
6.2.1 Intensité du courant
Au nœud A, le courant Ise divise en un courant I1qui traverse la branche renfermant R1et un
courant I2qui traverse la branche renfermant R2.AunœudB,lesdeuxcourantsserejoignent.
On a donc :
I=I1+I2
6.2.2 Tension
Toutes les charges qui se trouvent du côté gauche du circuit ont la même énergie. Il en est de
même pour toutes les charges qui se trouvent du côté droit du circuit. Si une charge de 1C
passe donc de la gauche vers la droite, la différence d’énergie(etdonclatension)estlamême,
peu importe la branche du circuit traversée :
U=U1=U2
6.2.3 Résistance
On se propose de remplacer deux résistances R1et R2en parallèle par une seule résistance Rtot.,
sans que l’intensité du courant électrique dans le circuit nechange:
112

6. LOIS DES CIRCUITS III. Electricité
R1
R2
I
I1
I2
I1
I2
I
U
U
U
BA
Rtot.
U
I I
Figure III.14 – remplacer deux résistances en parallèle par une seule résistance
En utilisant la loi d’Ohm, nous obtenons :
—pourlapremièrerésistance:
U=R1·I1
⇔I1=U
R1(1)
—pourladeuxièmerésistance:
U=R2·I2
⇔I2=U
R2(2)
—pourlarésistancetotale:
U=Rtot. ·I
⇔I=U
Rtot. (3)
Comme les intensités du courant s’additionnent :
I=I1+I2(∗)
En remplaçant (1), (2) et (3) dans (*), on obitent :
U
Rtot.
=U
R1
+U
R2
Après simplification par U, nous avons finalement :
1
Rtot.
=1
R1
+1
R2
Sui deux résistances sont branchées en série, alors l’inverse de la résistance totale est égal à la
somme des inverses des résistances individuelles.
113
1
/
4
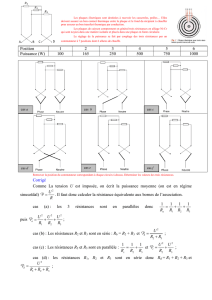
100%