Ondes électromagnétiques

Physique - 7 ème année - Ecole Européenne
Ecole Européenne de Francfort Page 81
Chapitre n° 7 : ONDES ELECTROMAGNETIQUES
I) Notion d’onde électromagnétique :
1) Introduction :
Dans la leçon précédente, nous avons considéré des ondes mécaniques comme, par
exemple, les vagues à la surface de l'eau. Il était assez facile de "visualiser" l'aspect
ondulatoire de ces ondes : surface d'onde, longueur d'onde.
Dans le cas des ondes électromagnétique et en particulier de la lumière, il est plus facile de
comprendre son aspect géométrique : direction de propagation, notion de rayon lumineux …
L'aspect ondulatoire de la lumière apparaît à travers l'interprétation des expériences.
2) Description ondulatoire :
a) Représentation schématique :
Une onde ou radiation électromagnétique constitue la propagation de la vibration d'un
champ électrique
→
E
et d'un champ magnétique
→
B
.
A un instant donné, on peut représenter schématiquement un état
d'une onde électromagnétique (polarisée et monochromatique)
en différents points de l’axe de propagation
(direction le long de laquelle
l'onde se propage) :
Sur le schéma très simplifié, ci-dessus :
- le champ électrique
→
E
(ou le champ magnétique
→
B
) varie de façon sinusoïdale le long
de l'axe de propagation : on a donc affaire à une onde monochromatique (une seule
fréquence, une seule couleur) : Ey(t) = Em.
- le champ électrique
→
E
(ou le champ magnétique
→
B
) "vibre" dans un seul plan : on a
donc affaire à une onde polarisée (verticalement, ici, pour le champ électrique).
Remarque : Il existe d'autres modes de polarisation de la lumière dont
nous ne parlerons pas dans ce cours
Remarque : Les cellules visuelles de la rétine (cônes et bâtonnets)
ne sont sensibles qu'à la vibration du champ électrique.
Dans la suite lors de l'étude d'une onde électromagnétique, nous ne
considèrerons que la propagation du champ électrique.
La lumière naturelle est formée d'ondes dont les vibrations du champ
électrique ont lieu dans tous les plans passant par l'axe de propagation.
Nous admettrons que l'intensité lumineuse L d'une onde est proportionnelle au carré de
l'amplitude Em du champ électrique : L = α.Em2.
champ électrique
propagation
vers
l'observateur
champ magnétique
axe de propagation
propagation vers
l'observateur

Ondes électromagnétiques
Page 82 Christian BOUVIER
Remarque : Attention : il ne faut pas confondre la lumière polarisée rectilignement, dont le
plan de vibration est unique, avec la lumière monochromatique, dont la
vibration est sinusoïdale et ne contient donc qu'une seule radiation.
Remarque : Attention : il ne faut pas confondre la lumière naturelle dont les vibrations ont
lieu dans tous les plans, avec la lumière blanche dont les vibrations sont la
superposition de toutes les radiations visibles (contenant toutes les couleurs,
toutes les fréquences du spectre visible).
Remarque : Une lumière peut donc être, soit naturelle et blanche, soit naturelle et
monochromatique, ou polarisée rectilignement et blanche, ou polarisée
rectilignement et monochromatique (cas de la figure ci-dessus).
b) Célérité (ou vitesse) de propagation :
Par convention la célérité d’une radiation dans le vide est : c0 = 299792458 m.s−1.
Nous utiliserons la valeur approchée c0 ≈ 3,00.108 m.s−1.
Dans les milieux transparents, la célérité de la lumière est plus faible que dans le vide.
c) Fréquence et longueur d’onde :
- La fréquence ν d'une radiation est indépendante du milieu de propagation.
La fréquence ν ou la période T d'une radiation caractérise cette radiation ("couleur").
On a la relation : T = 1/ν et ν = 1/T T en s et ν en Hz
Une radiation monochromatique est une onde électromagnétique "pure" dont la vibration
du champ électrique (ou magnétique) en un point, est sinusoïdale à une fréquence ν.
La lumière blanche est une onde électromagnétique dont les vibrations du champ
électrique (ou magnétique) sont la superposition de toutes les radiations du spectre
visibles (contenant toutes les couleurs, toutes les fréquences du spectre visible).
- La longueur d'onde λ d'une radiation dépend du milieu dans lequel l'onde se propage.
Nous noterons λ0 la longueur d'onde d'une radiation lumineuse dans le vide et λ sa
longueur d'onde dans un milieu transparent.
Dans le vide on a la relation : λ0 = c0.T ou λ0 = c0/ν.
Dans un milieu transparent on a : λ = c.T ou λ = c/ν.
λ0 ou λ en m, T en s et ν en Hz
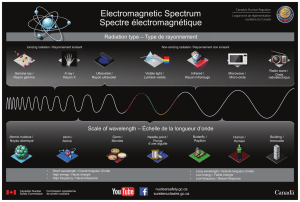
La fréquence des ondes visibles est comprise entre 3,75.1014 Hz = 375 THz pour le rouge
et 7,50.1014 Hz = 750 THz pour le violet.
Dans le vide ou dans l'air, pour les radiations visibles on a :
4.10−7 m = 400 nm (violet) < λ0 < 8.10-7 m = 800 nm (rouge)

Physique - 7 ème année - Ecole Européenne
Ecole Européenne de Francfort Page 83
II) Aspect géométrique de la propagation de la lumière :
1) Propagation rectiligne de la lumière :
Notre expérience quotidienne des ombres portées nous montre la propagation rectiligne de
la lumière émise par une source quasi-ponctuelle ou par le Soleil.
Nous admettrons que :
Dans un milieu transparent et homogène, la lumière se propage en ligne droite.
Remarque : La propagation rectiligne de la lumière du Soleil dans l'espace a permis à
Aristote (384 - 322 av. J.-C.) de concevoir la rotondité de la Terre : il a observé
que "lors des éclipses de Lune, l'ombre portée de la Terre a toujours pour limite
une ligne courbe, comme l'éclipse est due à l'interposition de la Terre, c'est la
forme de la surface de la Terre qui est cause de la forme de cette ligne".
La propagation rectiligne de des rayons solaires explique les différents aspects, lors d'une
éclipse de Soleil :
Schématisation d'un faisceau lumineux :
(ondes sphériques (ondes planes) (ondes sphériques
divergentes) convergentes)
Remarque : Si r est petit on parle de pinceau lumineux.
un faisceau lumineux est constitué d'un ensemble de rayons lumineux.
Il est impossible, expérimentalement, d'isoler un rayon lumineux (à cause du
phénomène de diffraction).
Remarque : Un rayon laser pourra modéliser un rayon lumineux.
2) indice de réfraction :
On a vu que la célérité des ondes électromagnétiques dans le vide était :
c0 = 299792458 m.s−1 ≈ 3,00.108 m.s−1.
Dans un milieu transparent, la célérité c de la lumière est inférieure à c0.
L'indice de réfraction n d'un milieu transparent par rapport au vide est défini par :
n =
c
c0
Exemple : Le tableau ci-dessous donne l'indice de réfraction de quelques substances :
air eau huile verre Crown verre Flint carbone
1,0002 1,333 1,5 1,517 2,417 2,76
éclipse totale
éclipse partielle
terminateur zone d'ombre

Ondes électromagnétiques
Page 84 Christian BOUVIER
3) Les lois de Descartes :
On considère un rayon lumineux incident
SI qui passe d'un milieu (1), d'indice de
réfraction n1, à un milieu (2), d'indice de
réfraction n2, en traversant un dioptre plan.
Le plan d'incidence est défini par le
rayon d'incidence SI et la normale au
dioptre N'N' passant par le point
d'incidence I.
IR1 est le rayon réfléchi; IR2 le rayon
réfracté, i1 est l'angle d'incidence, r1
l'angle de réflexion et i2 l'angle de
réfraction. N'N' est la normale.
Remarque : si n1 < n2 le milieu 2 est plus
réfringent que le milieu 1 : le rayon
réfracté s'approche de la normale.
L'expérience montre que ;
- Le rayon incident, le rayon réfléchi et le rayon réfracté sont dans un même plan : le plan
d'incidence.
- Le rayon incident et le réfléchi sont tels que : r1 = i1
- Le rayon incident et le rayon réfracté sont tels que : n1.sini1 = n2.sini2
Dans le cas où n1 > n2 le milieu 2 est moins réfringent que le milieu 1 : le rayon réfracté
s'éloigne de la normale.
Si n1 > n2, il existe un angle d'incidence lime i1lim au-delà duquel un rayon incident est
totalement réfléchi : aucun rayon n'est transmis dans le milieu 2.
Si rayon arrive sous l'incidence limite i1lim, le rayon réfracté forme avec la normale un angle
i2lim = π/2 : on dit que l'onde réfractée est évanescente (elle se propage sur le dioptre).
incidence sous un angle i1 < i1lim
incidence limite I1 = i1lim
i1 > i1lim réflexion totale
onde évanescente
onde réfractée avec i2 > i1
Exemple : La propriété d'incidence limite est utilisée dans les "prismes à réflexion totale"
utilisés dans les jumelles de vision.
La transmission d'informations par les fibres optiques utilise également cette
propriété de réflexion totale (voir exercice "pour s'entraîner").
Remarque : Nous avons vu dans la leçon précédente qu'il était possible de retrouver les lois
de la réflexion et de la réfraction (lois de Descartes) en faisant appel aux
caractères ondulatoires (longueur d'onde, surface d'onde).

Physique - 7 ème année - Ecole Européenne
Ecole Européenne de Francfort Page 85
4) Dispersion de la lumière :
a) Définition :
Nous avons vu dans la leçon précédente qu'un milieu de propagation est dispersif quand
la célérité c de propagation d’une onde dépend de sa fréquence.
En optique, on s'intéresse à l'indice de réfraction d'un milieu transparent.
Un milieu transparent est dispersif quand son indice de réfraction dépend de la fréquence
ν de l'onde qui le traverse : n = f(ν)
b) Etude de la dispersion par un prisme :
En optique, un prisme est un milieu transparent limité par deux faces planes non
parallèles, se coupant suivant une droite appelée arête du prisme.
Un plan perpendiculaire à l'arête est appelé plan de section principale. La face opposée
de l'arête est la base du prisme.
L'angle A opposé à la base est l'angle du prisme.
- En lumière monochromatique :
On éclaire une face du prisme à l'aide d'un faisceau laser (radiation monochromatique) :
* Le faisceau est dévié par le prisme.
* Quand on fait tourner le prisme autour d'un axe
parallèle à son arête, on constate que la déviation D
du faisceau varie.
* Pour une certaine valeur de l'angle
d'incidence i du faisceau sur la face
d'entrée du prisme, la déviation D passe
par un minimum.
On considère un rayon de lumière
monochromatique arrivant avec l'incidence
i sur la face d'entrée du prisme.
A la traversée du dioptre le faisceau subit une réfraction. L'angle de réfraction est r.
D'après les lois de Descartes, sin(i) = n.sin(r), où n est l'indice du verre par rapport à l'air.
A l'arrivée sur la face de sortie, le pinceau fait un angle d'incidence r' et un angle de
réfraction i' tels que : sin(i') = n.sin(r')
On vérifie que, géométriquement : r + r' = A
L'angle de déviation D est l'angle entre le pinceau incident et le pinceau émergent :
Or : D = (I – r) + (I' – r')
donc : D = (I + I') – (r + r')
soit : D = (i + i') – A
- En lumière blanche :
En lumière blanche, sur un écran, on constate que le
faisceau donne une tache lumineuse large et irisée.
On obtient le spectre de la lumière blanche.
Le bleu est la couleur la plus déviée par le prisme.
L'angle d'émergence i' du pinceau dépend de
l'indice du prisme, la déviation du pinceau
dépend donc de l'indice du prisme.
Toutes les radiations n'étant pas déviées du
même angle, nous en déduisons que l'indice
de réfraction du verre n'est pas le même pour
toutes les radiations.