musique et mathematiques _article

Musique et mathématiques : pour une orientation de recherche.
Le domaine de la connaissance humaine aura subi bien des évolutions au cours des siècles.
Unifié dans un même but, l’anticipation des intentions divines dans la Grèce antique, il se
trouve aujourd’hui subdivisé en spécialités définies, toujours plus nombreuses. Les différentes
disciplines qui le composent sont souvent dissociées en catégories, et les avancées
technologiques, qui agrandissent le champ de la recherche, génèrent la nécessité de définir,
encore et toujours, de nouvelles branches à l’arbre
1
de la connaissance.
Dans ce vaste champ, les domaines des arts, d’un côté, et des sciences, de l’autre, sont rarement
mis en relation. Les mathématiques, en tant que science pure, peuvent trouver une idée de
définition dans certaines lignes de pensée récentes
2
. Celles-ci sont structurées, formelles, et
d’un langage spécifique qui les rend difficiles d’accès. Elles sont pourtant au moins aussi
anciennes que l’humanité elle-même. A dire vrai, les mathématiques ne semblent pas être très
populaires de nos jours, contrairement à la musique, qui bénéficie d’une diffusion extrêmement
large et d’une facilité d’accès hors normes. L’activité musicale, d’ordinaire, représente, quant à
elle, l’art d’engendrer des émotions en atteignant la dimension transcendantale de l’homme, et
toute civilisation, sans exception, présente un aspect musical propre à sa culture. L’universalité
caractérise largement ces deux disciplines, mais ne suffit pas à les lier véritablement.
Des recherches fondamentales sur la musique et les mathématiques jalonnent l’histoire de
l’homme, et ce, depuis les plus anciennes réflexions de la philosophie occidentale. De
nombreuses théories tentèrent de véritables explications de l’ordre du monde par une harmonie
déterminée mathématiquement, et d’autres, eurent l’audace de soumettre la musique aux
mathématiques. Ainsi, au XVII
e
siècle, Gottfried Wilhem von Leibniz (1646-1716), ira jusqu’à
affirmer que la musique est une arithmétique inconsciente de l’esprit humain
3
.
L’importance profonde de ces deux disciplines, conjointement, et le rôle qu’elles ont à jouer
dans le développement de l’esprit humain ne va pas de soi. Il est donc absolument nécessaire
de retracer l’évolution la plus probable, compte tenu des fragments historiques, du lien qui les
uni fondamentalement à travers les investigations, passions et découvertes de l’homme.
1
« Toute la philosophie est comme un arbre, dont les racines font la métaphysique, le tronc est la physique, et les
branches qui sortent de ce tronc sont toutes les autres sciences qui se réduisent à trois principales, à savoir la
médecine, la mécanique et la morale, j'entends la plus haute et la plus parfaite morale, qui, présupposant une
entière connaissance des autres sciences, est le dernier degré de la sagesse », in Descartes, Principes de la
philosophie, Vrin, 2000, p. 42.
2
Friedrich Ludwig Gottlob Frege (1848-1925), mathématicien, logicien et philosophe allemand, donne une
définition logiciste des mathématiques en proposant de dériver l’arithmétique de la logique. Son contemporain et
correspondant Bertrand Russel (1872-1970), épistémologue, mathématicien, logicien, philosophe et moraliste
britannique, attribue aux mathématiques une valeur de vérité, et postule l’existence des entités mathématiques,
indépendamment de l’esprit humain, mais aussi de la réalité.
3
« L'ame compte les battements du corps sonnant qui est en vibration, et quand ces battements se rencontrent
regulierement à des intervalles courts, elle y trouve du plaisir. Ainsi elle fait ces comptes sans le savoir. C'est
ainsi qu'elle fait encore une infinité d'autres petites operations tres justes, quoyqu'elles ne soyent point
volontaires ny connues que par l'effet notable où elles aboutissent enfin, en nous donnant un sentiment clair mais
confus, parceque ses sources n'y sont point apperçues. Il faut que le raisonnement tache d'y suppléer, comme on
l'a fait dans la Musique, où l'on a decouvert les proportions qui donnent de l'agrement. ». « Musica est
exercitium arithmeticae occultum nescientis se numerare animi » : « la musique est une pratique cachée de
l'arithmétique, l'esprit n'ayant pas conscience qu'il compte », in Patrice Bailhache, Leibniz et la théorie de la
musique, Klincksieck, 2000, p. 151.

Une approche historique : de Pythagore à Bach
Cette idée de relation entre la musique et les mathématiques est un domaine extrêmement large
qui n’a cessé de s’enrichir depuis les plus antiques recherches scientifiques et philosophiques.
En effet, les passions que déchaîne l’art musical et les sciences mathématiques ne datent pas
d’une époque récente, bien au contraire. La fiabilité des sources permet de remonter à
l’antiquité les premiers esprits avertis.
C’est donc aux alentours du VI
e
siècle avant J.-C., sur Pythagore de Samos (570-500 av. J.-C.),
que se focalise la pensée de l’historien. Le contexte d’évolution des savants et philosophes
grecs, souvent confondus, présentait un aspect de la connaissance très différent de celui régnant
aujourd’hui. Le monde et les questions fondamentales soulevées par son observation étaient la
préoccupation première. Anticiper les décisions du divin devenait ainsi la priorité des sciences,
en toute évidence, mais aussi, plus étrangement, celle des arts. Ces activités humaines
possédaient donc un dessein identique, et des similitudes, car il est bon de rappeler que les
frontières conventionnelles auxquelles les modernes sont habitués, n’étaient pas strictement
ancrées et catégorisées. Le monde des Grecs recelait tant de mystères que la recherche de lois
et de principes d’un ordre était une nécessité.
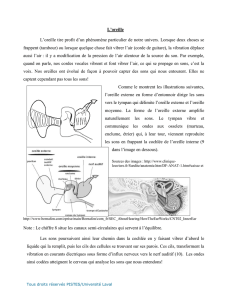
Dans cette perspective, la détermination des intervalles musicaux fut réalisée. Pythagore aurait
eu une ébauche d’idée, en observant l’atelier d’un maréchal-ferrant, dans une science
mathématique
4
imprégnée de la théorie des rapports entre les grandeurs et plus tard de la
« découverte » des irrationnels. Le mathématicien remarqua que les hauteurs des sons émis par
différents marteaux sur une même enclume pouvaient être mis en relation avec la masse propre
de chacun d’eux. Par expérience, il constata que des intervalles musicaux étaient égaux lorsque
des rapports de masses l’étaient aussi. C’est sur le rapport de la masse la plus lourde sur la plus
légère que Pythagore a établi son système. Un exemple simple : si l’enclume était d’abord
frappée avec un premier marteau de masse m et ensuite avec un autre marteau de masse 2m,
donc deux fois plus lourd, un rapport 2 serait considéré, et les deux sons obtenus seraient dans
un rapport d’octave
5
, le marteau le plus léger tirant la note la plus aigue. Pour un rapport de
3/2, avec un marteau de 4kg et un autre de 6kg par exemple, l’intervalle musical est une
quinte
6
. Cette observation permit à Pythagore de tester cette loi sur une sorte de tympanon, un
instrument appelé monocorde
7
. Autre constatation, les vibrations des cordes produisaient des
sons musicaux harmonieux pour l’oreille humaine lorsque le rapport de la plus grande longueur
4
Les éléments d’Euclide, dans l’antiquité grecque, présente un agrégat de la plupart des grandes idées
mathématiques de la période -300 av. J.-C. Véritable encyclopédie mathématique, elle est une des principales
sources historiques d’importance et de fiabilité relativement grande. Y apparaissent les idées fondamentales de
proportionnalité, et implicitement, de rapport, aux livres V et VII, respectivement.
5
L’octave est l’intervalle situé entre deux sons musicaux dont les fréquences fondamentales sont dans un rapport
double. La reconnaissance de cet intervalle, à l’oreille humaine, est universelle, et si évidente qu’elle est à
l’origine de l’attribution des noms des notes. Par exemple, la fréquence 440Hz, celle du diapason, correspond à
la note la, et ainsi, les notes de fréquences 880 Hz et 220 Hz, seront aussi appelées La.
6
Le mot quinte désigne, grossièrement, l’intervalle que l’on trouve généralement entre cinq notes. Plus
exactement, la quinte est l’intervalle qui sépare deux sons dont les fréquences fondamentales sont dans un
rapport 3/2. Autrement dit, la note la plus aigue présente trois vibrations lorsque la note le plus grave n’en
présente que deux. Mise à part l’octave, la quinte est considérée comme l’intervalle consonant par excellence,
c'est-à-dire celui dont la combinaison des sons est la plus proche de la pureté, donc la plus remarquable à
l’oreille.
7
Le monocorde ne possède qu’une seule et unique corde montée sur trois taquets, dont l’intermédiaire,
s’apparentant à un chevalet mobile, permet de faire varier la longueur de la corde et ainsi la hauteur de son
désirée. Dans cette vérification expérimentale, la longueur de la corde remplace la masse des marteaux, et les
rapports entre les longueurs que le troisième taquet permet de déterminer, correspondent aux intervalles.

sur la plus petite donnait un entier. L’inexplicable devenait mystique, et les disciples de
Pythagore auraient ainsi véhiculé une forme de philosophie suivant laquelle les nombres
pouvaient conférer à l’art musical, et au monde en général, pureté et intelligibilité.
Mais c’est la contribution de Platon (427-348 av. J.-C.) qui détermina l’avenir de cette
découverte capitale, et pas seulement pour la musique, les mathématiques et le rapport entre ces
deux disciplines, mais pour le déploiement du savoir tout entier. Il lui appartient d’avoir sauvé
cette découverte de toutes considérations ésotériques évidentes. Cette loi ne fait pas partie du
domaine mystique, et n’est pas non plus une simple curiosité. Elle s’intègre dans l’ordre
immanent des choses. Le monde aura ainsi, pendant près d’une vingtaine de siècles, une
justification cohérente et véritablement scientifique, appuyée par le sens que Platon aura donné
à la découverte de Pythagore. Platon participera d’un nouveau développement de la théorie des
intervalles musicaux. Il mettra en place, en s’appuyant sur ce que les Anciens postulaient au
sujet des mouvements et trajectoires des corps célestes, la célèbre Musique Des Sphères
8
. Ce ne
sont évidemment pas des lois universelles que le philosophe a laissées en héritage, mais il aura
ainsi fait régner ses idées pendant des milliers d’années.
Quelques siècles plus tard, la musique est à nouveau présente aux côtés des mathématiques et
sa place est considérable. Interpréter et comprendre les signes que Dieu envoie est une leçon
qui s’appliquera à nouveau aux apports de la science grecque. Ainsi se répandra
l’enseignement, au XII
e
siècle, des monastères aux écoles, et il apportera au monde la mise en
avant des disciplines fondamentales du savoir, le Quadrivium : l’Arithmétique, l’Astronomie,
la Géométrie, et la Musique.
La philosophie et la science grecques auront une autorité telle à travers les âges que leur remise
en question n’apparaîtra qu’en fin de XIX
e
siècle. Ce système trop rigide aura un succès qui
engendrera son propre processus de remise en cause. La vision antique du monde ne saura faire
preuve d’adaptation face à la cohérence nécessaire entre théorie et expérience. La différence
flagrante entre le système de Platon et le réel ne pu donc se taire plus longtemps. Les planètes
ne suivaient pas rigoureusement les trajectoires qui leur était attribuées, et les sons musicaux,
de leur côté, ne vérifiaient pas strictement le système établi. Pour ne donner qu’un exemple, la
succession des quintes n’engendrait pas une suite cyclique, et pendant de très nombreux
siècles, confondre une note altérée
9
par un dièse et celle qui la suit directement sur un clavier,
comme do # et ré b, par exemple, eut un rôle d’une importance sans précédent sur la vie
musicale.
Il faudra attendre le XVII
e
siècle pour voir apparaître une des premières solutions à cet
imposant problème. C’est Andreas Werckmeister
10
(1645-1706), qui enclencha le bon procédé.
Il présenta une technique d’accord d’un clavier, en gardant l’écart de fréquences entre les notes
mi# et fa comme constante. Il attribue ensuite de manière égale cet écart sur les douze degrés
de la totalité chromatique. Ainsi apparaît une notion très précieuse en théorie de la musique : la
8
La théorie de la musique des sphères, ou encore l’harmonie des sphères, se base sur l’intuition que le monde est
soumis à des lois dictées par des rapports mathématiques harmonieux, et que, dans un modèle géocentrique de
l’Univers, les planètes comme Mercure, Mars, Jupiter, la Lune, Saturne, le Soleil, et Vénus, qui sont des sphères
fixes, sont liées à des proportions musicales, et les distances qui les séparent, à des intervalles musicaux.
9
Les altérations sont symbolisées, en musique, par # et b. Le dièse augmente une note d’un demi-ton, et le
bémol la baisse d’un demi-ton.
10
Andreas Werckmeister, était un musicien allemand, organiste, expert en facture et théoricien de la musique. Il
est plus particulièrement connu, aujourd’hui, pour ses théories musicales et ses écrits : Musicae mathematicae
hodegus curiosus (1687), et Musicalische Temperatur (1691).

notion de tempérament
11
. En hommage au travail de Werckmeister, Bach (1685-1750)
composera le très célèbre Clavier bien tempéré. Cette œuvre, principalement théorique, aurait
eu pour unique but de mettre en avant les possibilités harmoniques qu’une détermination d’un
bon tempérament pouvait réaliser.
Il y eut énormément de conséquences, dont un fossé grandissant entre théorie musicale et
pratique musicale, mais également une considération différente des musiciens théoriciens,
comme étant, jusqu’au XVIII
e
siècle, les seuls véritables musiciens dignes de ce nom. Les
instrumentistes, voire même les compositeurs, ne représentaient alors que de simples outils
aux mains du théoricien. Il n’y a rien d’étonnant à ce que le lien entre les sciences
mathématiques et l’art musical ait varié au cours du temps, à la façon d’une distance
physique, parfois trop proche et parfois trop lointaine. Il semble qu’à partir de l’instant où le
système des Anciens fut remis en cause, ces deux disciplines s’éloignèrent
significativement. Les théoriciens de la musique de l’époque de Werckmeister et du XVII
e
siècle, faisaient preuve de démarches scientifiques, mais cela ne suffisait pas à combler ce
fossé radicalement creusé au plus profond des mentalités.
La musique, les hommes de sciences, et la perfection chez Euler
Après l’époque médiévale, un grand nombre de savants s’intéressèrent à la musique. L’état
d’esprit platonicien demeurait vivant au sein de la communauté scientifique qui se penchait
sur les théories musicales. L’objectif, par des investigations orientées sur les systèmes
harmoniques, restait la découverte d’une vaste explication du monde. Le célèbre allemand
Johannes Kepler (1571-1630), connu dans le domaine de l’astronomie, affichera ses
influences marquantes dans De Harmonice Mundi, où se trouvent certains éléments du
Timée
12
de Platon. Un contemporain, Robert Fludd (1554-1637), qui affichait un jugement
sévère envers les thèses de l’astronome, considérées dans leur dimension naïve, tentera un
système différent
13
. Sans oublier, que, Sir Isaac Newton (1642-1727), pour sa part, n’était pas
si loin de ces idées, mais le domaine scientifique aura tôt fait d’épurer ses véritables objectifs.
Leibniz n’avait certainement en vue, d’après un bon nombre d’interprétations historiques, que
11
Le tempérament est un procédé musical qui nécessite des calculs mathématiques. L’octave se divise en 7 sous
intervalles, dont les notes do, ré, mi, fa, sol, la, si, do, en sont les bornes. Celui-ci peut aussi être divisé en 12
parties, chacune étant égale à un demi-ton. C’est le tempérament égal. Entendu comme égalisation des
intervalles de l’échelle sonore, de sorte que chaque intervalle soit égal ou équivalent à un multiple d’un intervalle
étalon qui est de l’ordre d’un douzième d’octave, le tempérament égal permet, à un pianiste par exemple, dont
l’instrument possède des sons fixes, de prendre n’importe quel son de l’échelle pour commencer une nouvelle
gamme. Le tempérament égal devait fonder un système qui donnait à la musique des règles précises et
universelles. Cette division en demi-tons égaux s’est effectuée en fonction des limites de ce que peut percevoir
l’oreille humaine. Cette dernière est sensible aux demi-tons, c'est-à-dire qu’elle fait la différence entre les notes
do et do#, par exemple. La division commune du tempérament égal ne convenait pas à d’éminents musicologues
et théoriciens de la musique, soucieux de l’exactitude d’un découpage de l’octave en douzième d’octave. La
gamme tempérée, citée dans un traité de Werckmeister datant de 1691, trouve ses origines au cours du XVII
e
siècle, et ce dans un but purement rationnel et pratique. Les principaux tempéraments inégaux se trouvent au
XVIII
e
siècle. Le but est d’améliorer la qualité des tierces, des quintes, et des modulations. Les possibilités, dans
la recherche du tempérament inégal idéal, sont en nombre infini, et il n’en existe évidemment pas une seule
qui soit parfaite. La seule alternative est celle du choix de l’un d’entre eux qui serait plus avantageux que les
autres, relativement à l’œuvre musicale envisagée. Cette notion est étroitement liée au concept de subjectivité.
12
Le grand astronome Johannes Kepler reprend les thèses de Platon en s'émerveillant de la musique des Sphères.
Le modèle musical doit décrire le monde des sons, mais bien plus encore l'univers lui-même. La musique, les
mathématiques et la philosophie sont alors entrecroisés dans un même but.
13
Dans ses livres, Robert Fludd cherche à trouver une harmonie entre le monde et l'homme. Il s’intéresse à
l’harmonie entre les planètes, la musique, le corps humain et les anges dans Monochordium Mundi
symphoniacum J. Kepplero oppositum (1622).

la musique comme système scientifique le plus adéquat. De grands hommes de sciences de
renommées indiscutables et de découvertes bien souvent fondamentales dans l’histoire de
l’évolution humaine, ne peuvent que caractériser un argument d’autorité pour une ligne de
pensée vers laquelle il semble alors judicieux de se tourner.
L’idée d’arithmétisation de la musique est en train de germer chez Euler (1707-1783) et va
garder les bases des principes grecs. C’est en 1739 qu’il publie, en latin, son Essai d’une
nouvelle théorie de la musique exposée en toute clarté selon les principes de l’harmonie les
mieux fondés
14
. Tout, en musique, repose sur les mathématiques, et la notion d’agréable à
l’oreille humaine également. En effet, certains sons peuvent provoquer du plaisir, paraître
harmonieux. S’ils le sont, c’est parce qu’ils nous révèlent la perfection. « Il est certain que
toute perfection fait naître le plaisir et que c'est une propriété commune à tous les esprits,
aussi bien de se réjouir à la découverte et la contemplation d'un objet parfait, que d'éprouver
de l’aversion pour ce qui manque de perfection ou que des imperfections dégradent. »
15
C’est
sur cette base que s’appuie la théorie d’Euler : la sensation d’agréable devient alors un indice
de perfection. Et cette dernière se réduit à l’ordre
16
, entendu comme agencement et
combinaison entre les notes. L’ordre est une notion fondamentale dans cette recherche de
règles mathématiques inhérentes à la musique et à sa perception par l’homme. Il se définit par
rapport à deux sortes de caractéristiques : la hauteur des notes, c’est-à-dire si elles sont graves
ou aigues, et la durée de celles-ci.
Selon Euler, le plaisir musical trouve donc son explication dans la mesure arithmétique des
proportions liées aux sons. Le mathématicien utilise, d’une part, les rapports de fréquences de
plusieurs sons
17
, ce qui représente une démarche scientifique, d’une autre, il justifie leur
existence et leur rôle dans la sensation de plaisir par des arguments philosophiques. Euler ne
retient pas la durée lorsqu’il met en place sa notion de « degré de douceur »
18
. Euler attribue
un rapport mathématique à chaque ordre de sons, comme la tradition antique l’avait élaboré.
14
Euler n’est âgé que de 24 ans lorsqu’il écrit cet essai. L’intérêt qu’il porte à la musique n’a rien de ponctuel.
En 1727 sa ‘‘Thèse sur le son’’ présente des comparaisons entre les notes émises par un instrument à vent, et
celles émises par un instrument à cordes. La notion de timbre, coloration propre à un instrument ou à une voix,
apparaît alors déjà dans sa vision musicale.
15
Euler, Essai d'une nouvelle théorie de la musique, Oeuvres Complètes en Français, Association des capitaux
intellectuels pour favoriser le développement des Sciences Physiques et Mathématiques, tome 5.
16
« Prenons pour exemple une horloge, dont la destination et de marquer les divisions du temps ; elle ne plaira
au plus haut degré, si l'examen de la structure nous fait comprendre que les différentes parties en sont disposées
et combinées de telle manière que toutes concourent à indiquer le temps avec exactitude. Ainsi, dans toute chose
où il y a de la perfection il y a nécessairement aussi de l'ordre », in Euler, Essai d'une nouvelle théorie de la
musique, Oeuvres Complètes en Français, Association des capitaux intellectuels pour favoriser le développement
des Sciences Physiques et Mathématiques, tome 5.
17
Les sons, comme vibrations de l’air, parviennent à l’oreille en provoquant des pressions régulières, ou des
coups, sur le tympan. Le nombre de vibrations par seconde s’appelle la fréquence, mesurée en Hertz, et
caractérise la hauteur d’une note. Plus le nombre de vibrations est élevé plus la note paraîtra aigue. Euler avait
conscience de l’idée de coups imposés au tympan. Celui-ci imaginait de petits corpuscules sonores régit par une
loi des chocs dans le milieu de propagation des sons. L’expression « numeri vibrationum » qui apparaît dans
l’essai original, permet une interprétation moderne en termes de fréquences et de « nombre de vibrations ».
18
Euler va faire le lien entre mathématique et musique : le degré de douceur est un nombre entier attribué à un
ou plusieurs intervalles musicaux. Plus le degré de douceur est petit, plus l’intervalle musical correspondant sera
consonnant et proche de la perfection. Le degré de douceur permet ainsi un classement des accords
fondamentaux.