Autres propriétés

Séquence 4 : Quadrilatères particuliers • RÉSUMÉ •
Des maths ensemble et pour chacun – 5e © CRDP des Pays de la Loire, Nantes, 2010. © CRDP des Pays de la Loire, Nantes, 2009.
Propriétés des quadrilatères particuliers
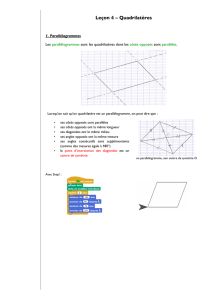
I- Parallélogramme
Définition
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Propriétés
Quand on sait qu'un quadrilatère est un parallélogramme, on peut affirmer que :
1. ses côtés opposés sont parallèles ;
2. ses côtés opposés ont la même longueur ;
3. ses diagonales ont le même milieu ;
4. ses angles opposés ont la même mesure ;
5. ses angles consécutifs sont supplémentaires ;
6. le point d’intersection des diagonales est
centre de symétrie.
O
Un parallélogramme
(un centre de symétrie O)
II- Losange
Définition
Un losange est un quadrilatère qui a quatre côtés de même longueur.
Remarque
Un losange est un parallélogramme particulier donc un losange a toutes les propriétés
d’un parallélogramme.
Autres propriétés
Quand on sait qu'un quadrilatère est un losange, on peut affirmer que :
1. ses côtés ont la même longueur ;
2. ses diagonales sont perpendiculaires ;
3. ses diagonales sont axes de symétrie ;
4. ses diagonales sont bissectrices des angles.
O
Un losange
(un centre O et deux axes de symétrie)

Séquence 4 : Quadrilatères particuliers • RÉSUMÉ •
Des maths ensemble et pour chacun – 5e © CRDP des Pays de la Loire, Nantes, 2010. © CRDP des Pays de la Loire, Nantes, 2009.
III- Rectangle
Définition
Un rectangle est un quadrilatère qui a quatre angles droits.
Remarque
Un rectangle est un parallélogramme particulier donc un rectangle a toutes les propriétés
d’un parallélogramme.
Autres propriétés
Quand on sait qu'un quadrilatère est un rectangle, on peut affirmer que :
1. ses angles sont droits ;
2. ses diagonales ont la même longueur ;
3. ses côtés opposés ont les mêmes médiatrices :
ce sont des axes de symétrie.
O
Un rectangle
(un centre O et deux axes de symétrie)
IV- Carré
Définition
Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur.
Remarque
Un carré est un rectangle particulier et un losange
particulier donc un carré a toutes les propriétés
d’un rectangle et d’un losange.
O
Un carré
(un centre O et quatre axes de symétrie)