6ème - juin-14 - Chap. n°33 : Quadrilatère, partie I

6ème - avr.-17 - Chap. n°33 : Quadrilatère, partie I - Page 1 / 15
Chapitre n°33 : Les quadrilatères, partie 1
Objectifs à atteindre :
a. 6ème : connaître et utiliser les propriétés relatives aux côtés
et aux angles du rectangle et du carré.
b. 6ème : connaître et utiliser les propriétés relatives aux
côtés, aux angles pour le losange.
Exercice n°1 – EXERCICE DIAGNOSTIQUE
Cet exercice est UN EXERCICE DIAGNOSTIQUE :
- Il faut essayer de le faire UNE SEULE FOIS.
- Il faut ensuite essayer de compléter le cours qui suit.
- Si tu as UNE erreur ou plus, ou si tu NE SAIS PAS REPONDRE, passe
A L’EXERCICE QUI SUIT.
- Si tu as TOUT JUSTE (vérifie-le en regardant les solutions à la fin du
document) et si le COURS EST JUSTE aussi (fais le vérifier par le
professeur), va DIRECTEMENT à l’exercice n°4
- ATTENTION : tu peux quand même avoir une interrogation sur le
cours.
1. Construire un carré HGUI tel que UI=4 cm.
2. Recopier et compléter :
a. [UI] est opposé à ……….
b. ;HGU est opposé à ………………
c. [GU] est consécutif à ……………….
d. [HU] est une ………………………..
e. [IH] et [IU] sont ………………………….
f. [IH] et [UG] sont …………………………
g. H et U sont ………………………………….
h. ;HGU et ;GUI sont …………………………….
i. Ce carré peut s’appeler G……………

6ème - avr.-17 - Chap. n°33 : Quadrilatère, partie I - Page 2 / 15
Exercice n°2 – INTRODUCTION AU COURS N°1 – INDISPENSABLE POUR
COMPLETER LE COURS. – Vocabulaire
Dans un quadrilatère :
 Les côtés qui sont en face l’un de l’autre s’appellent des côtés
opposés.
 Les côtés qui se suivent s’appellent des côtés consécutifs.
 Les angles qui sont en face l’un de l’autre s’appellent des angles
opposés.
 Les sommets qui sont en face l’un de l’autre s’appellent des sommets
opposés.
 On nomme le quadrilatère en tournant autour (dans le sens des
aiguilles d’une montre ou dans le sens inverse).
 Les diagonales sont les droites qui passent par deux sommets
opposés.
1. En relisant les définitions ci-dessus, complétez la figure ci-dessous :
2. Compléter :
Ce quadrilatère se nomme ABCD ou ADCB ou B……… ou B……… etc.
Ce quadrilatère se nomme …………ou ………… ou …………ou ………… etc.
A
B
C
D
F
J
R
K
Ces 2 angles
sont ………………
Ces 2 côtés sont
………………….
Ces 2 côtés sont
………………….
(AC) est une
………………….
Ces 2
………………… sont
………………….

Sixième : Chapitre n°27 : Quadrilatère - Page 3 / 15
Cours n°1---------------------------------------------
Cours à compléter, à montrer au professeur :
Chapitre n°33 : Quadrilatères, partie 1
Vocabulaire
Définition n°1 a.
 Les côtés, angles ou sommets qui sont ……… ……………………… l’un de
l’autre s’appellent des côtés, angles ou sommets ……………………...
 Les côtés, angles ou sommets qui …… ……………………. s’appellent des
côtés, angles ou sommets ………………………
Définition n°1 b.
 On nomme le quadrilatère en ………………………. …………………………. (dans le
sens des aiguilles d’une montre ou dans le sens inverse).
Définition n°1 c.
 Les diagonales sont les ………………………… qui passent par deux sommets
………………………………
Exemple n°1
En relisant les définitions ci-dessus, complétez la figure ci-dessous :
Fin du Cours n°1---------------------------------------
A
F
C
E
F
K
R
P
Ces 2 angles
sont ………………
Ces 2 côtés
sont
………………….
Ces 2 côtés
sont
………………….
Ces 2
…………………sont
………………….
(AC) est une
………………….
Ce quadrilatère se nomme
ABCD ou ADCB ou B……… ou
B……… etc.
Ce quadrilatère se
nomme …………ou
………… ou …………ou
………… etc.

Sixième : Chapitre n°27 : Quadrilatère - Page 4 / 15
Apprentissage du cours
Copier les savoirs, de mémoire, 6 fois, sur une feuille de brouillon, en « accordéon ».
Coller l’accordéon, plié, dans votre cahier de cours (attention : le professeur peut vous
demander de montrer ce travail)
Recopier le cours dans le cahier de cours (à la maison !) – Penser à changer
de page (nouveau chapitre)
Contrôle du savoir faire :
Refaites les exemples du savoir faire ci-dessous, sans regarder le cahier
de cours, puis contrôlez que vous avez juste.
Exemple n°1
En relisant les définitions ci-dessus, complétez la figure ci-dessous :
Le quadrilatère de gauche se nomme A……… ou A………ou C……… ou C……… etc.
Le quadrilatère de droite se nomme F………ou F……… ou K………ou K……… etc.
Exercice n°3
Le quadrilatère ci-contre est un rectangle.
1. Nommez-le : ……………………….
2. Quel est le côté opposé à [EC] ? ………………………
3. Citer un côté consécutif à [RT] : …………
4. Citer un sommet consécutif à R : …….
5. Quel angle est opposé à a;TCE ? ……………….
6. Citer un angle consécutif à a;RTC :…………….
7. Quel côté est à la fois consécutif à [CE] et opposé
à [TC] ? ………………………….
8. Citer deux diagonales de ce rectangle : ………………. et ………………….
Exercice n°4 – INTRODUCTION AU COURS N°2 – INDISPENSABLE POUR
COMPLETER LE COURS
Rechercher ou rappeler les deux propriétés de la symétrie axiale, et les
réécrire sur le cahier d’exercices.
A
F
C
E
F
K
R
P
Ces 2 angles
sont ………………
Ces 2 côtés
sont
………………….
Ces 2 côtés
sont
………………….
(AC) est une
………………….
Ces 2
…………………sont
………………….
R
E
C
T

Sixième : Chapitre n°27 : Quadrilatère - Page 5 / 15
Exercice n°5 – INTRODUCTION AU COURS N°2 – INDISPENSABLE POUR
COMPLETER LE COURS
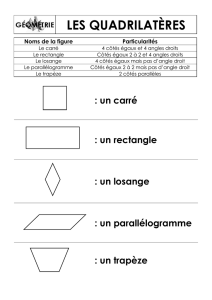
a. Complétez les légendes des figures ci-dessous avec « Carré », « Losange »,
« Rectangle » et « Trapèze ».
b. Construire les axes de symétries de chaque figure.
Exercice n°6 – le rectangle – INTRODUCTION AU COURS N°2 –
INDISPENSABLE POUR COMPLETER LE COURS
On veut dresser la « fiche d’identité » de chacun des quadrilatères de
l’exercice précédent.
Commençons par le rectangle :
a. Sur le rectangle ci-contre, tracez en rouge les axes de symétrie,
et en bleu les diagonales.
b. Complétez, en revoyant éventuellement le chapitre sur la
symétrie :
« Le symétrique d’un segment est ………………………………………………………
…………………………………………………. ».
« Le symétrique d’un angle est …………………………………………………………..
…………………………………………………. ».
c. Complétez avec des mots parmi « milieux », « deux »,
« opposés », « consécutifs » « symétrie », « égaux »,
« diagonales », « perpendiculaires », « parallèles »:
« Un rectangle a …… axes de ……………………….. qui passent par les
………………………………. des côtés. Donc, d’après la propriété de la
symétrie sur la longueur d’un segment et du symétrique de ce
segment, le rectangle a des côtés o…………………… é………………….. »
d. Complétez avec des mots parmi : « milieux », « deux »,
« opposés », « consécutifs » « symétrie », « égaux »,
« diagonales », « perpendiculaires », « parallèles »:
« Un rectangle a …… axes de ……………………….. qui passent par les
………………………………. des côtés. Donc, d’après la propriété de la
R
E
C
T
……………………
……………………
……………………
……………………
SUITE PAGE SUIVANTE